[! important] 重要提醒
- 需要梳理清楚某个重要因素对于其他的 FOM 的影响,或者根据 FOM 的变化找到其变化的原因。
- 如果 ppt 上讲的是 n 型,最好思考一下 p 型应该如何变化;
1. 半导体物理基础
1.1. 迁移率
迁移率
迁移率描述给定材料在平均电场作用下平均漂移速度,有定义式:
迁移率定义式
指向原始笔记的链接
为平均漂移速度; 为电场强度。 载流子迁移率计算
根据定义可以推导出,
电子迁移率公式
指向原始笔记的链接
是一个电子的带电量; 是电子的有效质量; 是电子的平均自由时间。 空穴迁移率公式
指向原始笔记的链接
是一个空穴的带电量; 是空穴的有效质量; 是空穴的平均自由时间。 与电子迁移率推导具有同样的推导过程
散射的影响
散射也会对迁移率造成影响。
我们设
为仅受杂质电离散射时的迁移率;设 为仅受晶格振动散射时的迁移率。 由此可得,在两种散射共同影响下的迁移率为
指向原始笔记的链接
1.2. 扩散系数
扩散系数
扩散系数是因分子扩散而产生的分子通量和分子浓度梯度之间的比例。
指向原始笔记的链接爱因斯坦关系
指向原始笔记的链接
是电子(空穴)的扩散率; 是电子(空穴)的迁移率; 是热电压,其在室温下的值为 。
1.3. 导带的有效状态密度
导带有效状态密度
导带有效状态密度(
)是半导体物理中的一个重要参数,用于描述导带中可以被载流子(电子)占据的量子态的密度。这个参数在计算载流子浓度、能带结构和许多其他半导体物理问题中起着关键作用。 导带有效状态密度计算式
指向原始笔记的链接
为电子的有效质量; 为波尔兹曼常数; 为开尔文温度; 为普朗克常数
1.4. 热平衡载流子浓度推导
这个就是热平衡载流子浓度的第一性原理,通过状态密度函数和费米-狄拉克分布函数积分推导出来的。
1.2.1.2. 状态密度函数
指向原始笔记的链接状态密度函数
状态密度函数表示为单位体积单位能量中的量子态数量(能态总数),是系统中状态的一个固有属性。
一般模型
首先讨论一个被束缚在三维无限深势阱中的电子,而这个势阱就代表晶体的有状态密度函数。
有效状态密度函数公式
指向原始笔记的链接
为电子的有效质量; 为普朗克常数; 为导带底的能量。 可以看出,量子态密度是能量
的函数,随着自由粒子能量的减弱,有效量子态的数量也逐渐减少。而且这个密度函数实际是双倍密度,也就是说,密度是在单位能量和单位体积中求得的。 推导看这里 半导体模型
将一般模型拓展到整个半导体,确定导带和价带中的量子态密度。
导带底的电子状态密度
有效状态密度函数公式
指向原始笔记的链接
为电子的有效质量; 为普朗克常数; 为导带底的能量。 价带顶的空穴状态密度
指向原始笔记的链接价带空穴状态密度函数计算式
指向原始笔记的链接
为空穴的有效质量; 为普朗克常数; 为价带顶的能量。
1.2.1.3. 费米-狄拉克分布函数
费米-狄拉克分布函数
费米-狄拉克分布函数代表了能量为
的量子态被电子占据的可能性,另一种含义是被电子填充的量子态占据总量子态的比率。一个量子态如果没被电子占据即为空,或者说被空穴占据,由此可以导出量子态被电子和空穴占据的总概率为 1。 费米-狄拉克分布函数公式
指向原始笔记的链接
能量为 处,被填充的能量状态密度; 为能量 处的总的能量状态密度; 为费米能级; 为波尔兹曼常数; 为开尔文温度。 快速计算技巧:
,能量每增加 60meV,概率增加一个数量级。当 时, 。
费米-狄拉克分布函数描述了在以费米能级为标准(50%,
),在其他能量态出现电子的概率。左边靠近价带,右边靠近导带。 特点
粒子不可分辨,每个量子态只允许一个粒子。
指向原始笔记的链接通过相乘并积分就能算出导带中电子和价带中的空穴。
指向原始笔记的链接[! note] 热平衡电子浓度
1.5. 热平衡条件
1.2.1.1. 热平衡载流子浓度
2021 #EE6604期末/2022 #EE6604期末/2023
通过导带顶、价带底、费米能级以及导带有效状态密度和价带有效状态密度,能分别计算出导带和价带中的载流子热平衡浓度
导带电子热平衡浓度公式
指向原始笔记的链接
为导带有效状态密度; 为导带底能量; 为费米能级; 为波尔兹曼常数; 为温度 价带空穴热平衡浓度公式
指向原始笔记的链接
是价带有效状态密度, 是价带顶能量, 是费米能级, 是玻尔兹曼常数, 是温度。 在载流子状态密度函数的计算中,导带和价带的有效状态密度是状态密度函数和费米-狄拉克分布函数相乘后在对应能带内的积分后得到的数学过程定义参数,无物理推导过程。后对状态密度函数和费米-狄拉克分布函数进行说明。
指向原始笔记的链接
在半导体物理中,质量作用定律(Law of Mass Action)描述了本征载流子浓度与电子和空穴浓度之间的关系。
1.2.1.4. 本征载流子浓度
2021 #EE6604期末/2022
指向原始笔记的链接本征载流子浓度
在本征半导体中,由电中性原理可知,导带中的电子浓度
等于价带中的空穴浓度 。因此通常用 来指代本征载流子浓度,它指热平衡电子浓度或者空穴浓度。 计算公式
本征载流子浓度计算式
指向原始笔记的链接
为导带有效状态密度; 为价带有效状态密度; 为禁带宽度; 为波尔兹曼常数; 为开尔文温度
为禁带宽度,硅为 ,碳化硅为 ; 时, 。 适用条件:1. 热平衡状态;2. 非简并(轻掺杂) 对于一个给定的半导体材料, 的值和温度强烈相关而和费米能级无关。 质量作用定律
对于任何热平衡状态下的半导体,有
这个是热平衡状态半导体的一个基础公式,是在玻尔兹曼近似的基础上推导而来的。
指向原始笔记的链接
1.6. 波尔兹曼关系
1.2.2.3. 波尔兹曼关系
波尔兹曼关系就是用费米势去表示热平衡载流子浓度。费米势定义为,
费米势定义式
指向原始笔记的链接
为费米能级; 为电子电荷。 [! note] 这里可以辅助理解外在电压是如何影响费米能级变化的。你施加正电压导致费米势增加,从而导致费米能级的降低。
用上面的式子代换到计算 N 型半导体和 P 型半导体的费米能级的公式中去(这里用掺杂浓度
近似了多子浓度 ) 波尔兹曼关系
指向原始笔记的链接
1.7. 载流子复合机理
1.2.4. 载流子复合
当载流子浓度从平衡状态受到扰动时(如受到光照或从结点注入),载流子浓度会自然回归到平衡值。这是因为平衡态是能量最低、最稳定的状态。这种恢复平衡的过程涉及过剩载流子的复合。
这里讲一讲最重要的 SRH 复合机理,这个机理同时适用于体内复合和表面复合。
指向原始笔记的链接SRH 复合
SRH 复合是
和 等间接带隙半导体的主要复合机制。 这种复合是非辐射的,载流子的过剩能量产生声子(晶格振动)。这涉及一个复合中心,一般是晶格缺陷,如位错(dislocations)、杂质原子(impurity atoms)。
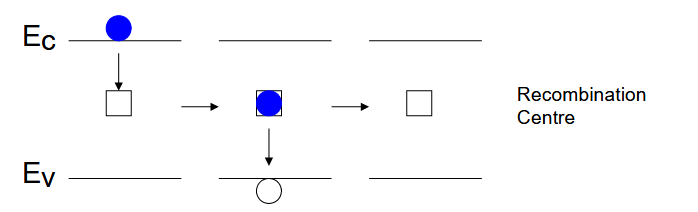
当复合中心处于最中间时复合率最高。
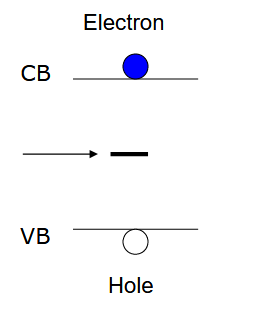
动力学原理
电子从导带到复合中心,随后再到价带与空穴复合,并产生声子损失能量。
对于 P 型硅中的小注入电子而言,
指向原始笔记的链接P 型硅体内复合率计算式
复 合 率 指向原始笔记的链接
为电子少子寿命; 为热平衡电子浓度; 为电子浓度
1.8. 表面复合
1.2.5. 表面复合
2022 #EE6604期末/2023
半导体晶体的表面布满缺陷,例如来自晶面末端的悬空键和来自环境的杂质。这些导致表面态的分布和表面附近的能带弯曲。因此,非辐射复合在非钝化半导体表面上会以更高的速率发生。
1.2.5.1. 表面复合速率
p 型半导体表面的复合率和体内复合率类似但是不同,
P 型半导体表面复合率
表 面 复 合 率 指向原始笔记的链接
为表面复合速度; 表面面积; 为电子浓度; 为热平衡电子浓度 [! note] 这里再说明一下「复合率」是个什么东西。 复合率就是单位时间内发生的复合事件次数,而一次空穴和电子合并然后产生声子就是一次复合事件。由此我们可以通过复合率来计算电流密度,P 型半导体表面复合电子电流密度计算式和 N 型半导体表面复合空穴电流密度计算式。
2. 硅 BJT
2.1. 紧凑模型的假设
2.2. 紧凑模型的假设
2021 #EE6604期末/2023
现做出以下假设:
指向原始笔记的链接
- 忽略所有的寄生电阻以及相关的压降;
- 忽略基极中发生的复合;
- 集电极电流仅由从发射极注入基极的电子产生;
- 基极电流由从基极注入到发射极的空穴产生。
2.2. 基极中电子电流密度
2.3.1. p 型基极中电子的电流密度方程
后面的公式都是在下面的 BJT 一维建模上进行的。
根据电子漂移电流密度公式、电子扩散电流密度公式、爱因斯坦关系式以及电场的定义,我们可以将在 P 型基极中的电子总电流密度公式重写为包含准费米能级的形式,
用准费米势表示 P 型基极中电子总电流密度推导过程用准费米势表示 P 型基极中电子总电流密度
指向原始笔记的链接
为电子电荷; 为基极中电子浓度; 为电子迁移率; 为电子准费米势 因为在基极中空穴准费米能级近乎恒定(因为 BJT 正偏时仅有空穴的复合会产生电流,但是基极的复合又是可以忽略的),于是有
,所以可以将上式再重写为, 考虑重掺杂效应,有,
[! question] 为什么不考虑大注入? CM 是这样假设的。
代入后得到,
这样就能通过基极电子和空穴浓度来计算基极中电流密度。 指向原始笔记的链接BJT 紧凑模型 P 型基极电子电流计算式
指向原始笔记的链接
为电子电荷; 为电子的扩散系数; 为有效本征载流子浓度; 为 p 型基极中空穴浓度; 为 p 型基极中电子浓度
2.3. 集电极电流
集电极电流密度是由上面基极中电子电流的密度,沿着基极中性区进行积分可得。
2.4.1. 集电极电流
2021 #EE6604期末/2023
有集电极电流为,
BJT 紧凑模型集电极电流计算式
指向原始笔记的链接 定义为饱和集电极电流密度, 集电极饱和电流密度
指向原始笔记的链接
为基区古梅尔数。 基极古梅尔数计算式
指向原始笔记的链接 [! note]
- 古梅尔数的定义考虑了基区重掺杂的影响。
- 集电极电流仅是基本参数的函数。
- 集电极电流不依赖于发射极的特性。
2.4. 发射极电流
2.4.2. 基极电流
由于没有电子复合,基极电流只是由基极到发射极的空穴注入电流构成。由于发射极的重掺杂,有
,于是可以把前面的 BJT 紧凑模型 N 型发射极空穴密度计算式重写, BJT 紧凑模型发射极空穴电流密度计算式
指向原始笔记的链接
为电子电荷; 为空穴的扩散系数; 为有效本征载流子浓度; 为 n 型发射极中空穴浓度; 为 n 型发射极中电子浓度。
2.5. 共基极电流增益和共发射极电流增益
2.6. 电流增益
共基极电流增益为,
共基极电流增益
指向原始笔记的链接
为集电极电流; 为发射极电流 共发射极电流增益为,
BJT 共发射极电流增益定义式
指向原始笔记的链接
为集电极电流; 为基极电流 通过将基极电流和集电极电流代换,能够得到
再代入两个古梅尔数的定义式,对于浅发射极有,
这样,通过掺杂浓度和发射极宽度就能直接计算得到共发射极电流增益。
再根据共基极电流增益和共发射极电流增益的关系,可以计算出,
共基极电流增益
指向原始笔记的链接
为集电极电流; 为发射极电流 一般情况下,
指向原始笔记的链接接近 1 并且小于 1,由此 会相当大,在目前的 VLSI 中,至少为 100。 作为 BJT 进行分析的品质因子,对于模拟应用非常重要。
2.6. 跨导
2.5. BJT 跨导
BJT 的跨导定义为,
BJT 跨导定义式
指向原始笔记的链接
为电子电荷; 为 BJT 集电极电流; 为波尔兹曼常数; 为绝对温度 BJT 跨导计算式
指向原始笔记的链接
2.7. 古梅尔图
2.8. 古梅尔图
2021 #EE6604期末/2023
古梅尔图
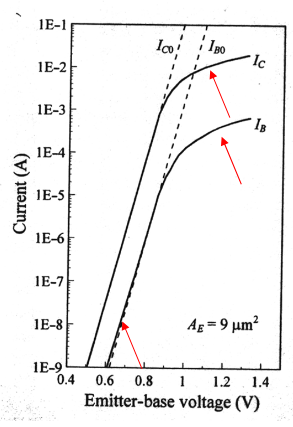
古梅尔图是双极型晶体管(Bipolar Junction Transistor, BJT)的一种常用特性曲线图,用于描述基极-发射极电压 VBE 与集电极电流 IC 和基极电流 IB 之间的关系。
versus 指向原始笔记的链接
只在 以及 均为线性的时候,才是常量。 可以看到在高 VBE 下,测得的 Ic 通常小于理想晶体管 (IC0)。在高 VBE 时,测得的 IB 通常也小于 IB0,但在低 VBE 时则高于 IB0。
[! summary] 这里总结一下实际电流和理想电流出现偏差的原因。原因的具体内容在 3. 非理想 BTJ 行为有叙述。
- 小注入时,
高于理想值
- 基极中的复合-产生电流
- 基极中的隧穿电流
- 大注入时,
低于理想值
- 发射极和基极的寄生电阻
、 和
- 大注入时,
低于理想值
- 发射极和基极的寄生电阻
- 基极电导调制效应
由此得到的共发射极增益
指向原始笔记的链接如下, 电流增益
与 IC 的关系不是恒定的。 仅在 IC 和 IB 接近理想的区域内保持恒定。对于小 IC,由于 IB 增加, 减小。对于大 IC, 减小,因为 IC 比 IB 减小得更快。
2.8. 基极调制效应
3.2. 基极电导率调制效应
这是导致 IC 在高
下降低的另一个效应。
- 在高水平的电子注入下,基极中的空穴浓度必须通过热生成而增加,以保持电荷中性(指电流连续性)。
- 此外,注入的电子会增加 BC结基极侧的负空间电荷。这减少了耗尽宽度并增加了准中性基极宽度
。
从上图可以看出,当大注入的时候,BC 结中基区的耗尽区的电子浓度更高,由此耗尽区宽度减小;而集电极的耗尽区空穴浓度降低,由此需要更宽的耗尽区。
基极古梅尔数计算式
指向原始笔记的链接 (1) 和 (2) 都增加了基极古梅尔数并降低了
指向原始笔记的链接。
2.9. 厄利效应
3.3.3. 厄利效应
2022 #EE6604期末/2023
指向原始笔记的链接厄利效应
厄利效应是指在具有轻掺杂薄基极 BJT 中,集电极电流通常随着集电极发射极电压的增加而增加。
这种效应是由基极集电极耗尽宽度的增加引起的。结果,准中性基底宽度 WB 减小。
厄利电压
厄利电压是描述双极型晶体管(BJT)中集电极电流随集电极-发射极电压 (
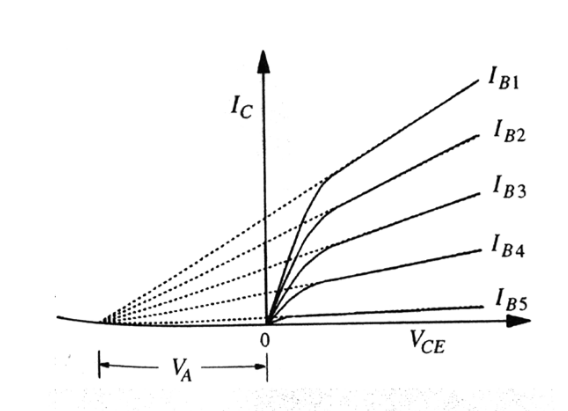
) 变化的敏感度的参数。它表征了 BJT 的输出特性曲线在理想情况下是否接近平坦,并间接反映了器件中电流增益的稳定性。 厄利电压非常大,至少 100V。集电极电流在线性区域内随 VCE 线性增加。当外推的集电极电流
等于 0 时的集电极电压称为厄利电压 。 厄利电压计算式
指向原始笔记的链接 小),准中性基极宽度会减小到零并发生穿通。 穿通也就是基极两边的耗尽区直接相接。指向原始笔记的链接
2.10. BJT 小信号交流模型
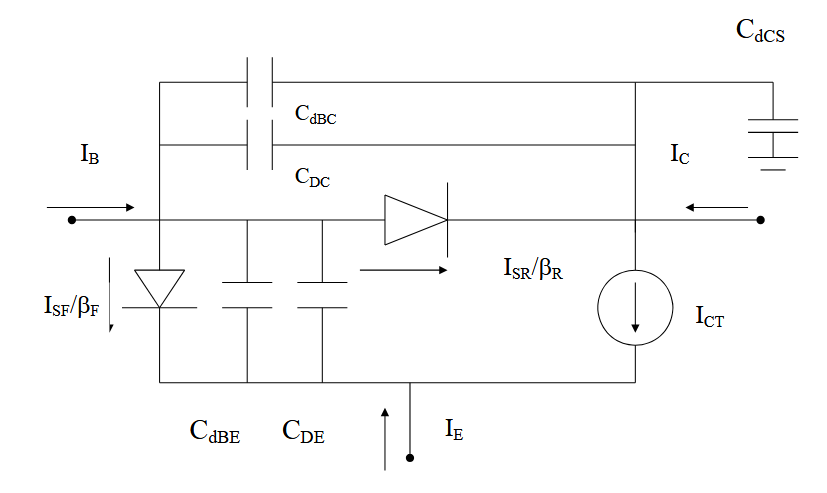
4.2. 双极晶体管的小信号交流模型
当存在交流信号时,必须将电容器添加到直流模型中。对于每个结而言,我们需要增加以下的电容器,
- 耗尽层电容,
- 扩散电容,
在共发射极 Embers-Moll 模型的基础上增加需要考虑的电容。
当小信号 (ss) 叠加在直流偏置电压上时使用。
后面会逐步推出如何从共发射极的 Ember-Moll 模型到这个模型
小信号基极电流 小信号集电极电流 小信号基极-发射极电压 小信号集电极-发射极电压 4.2.1. 模型参数
跨导
是直流偏置点处 相对于 的比值。参考公式 BJT 跨导计算式
指向原始笔记的链接 就能改变 。 输入阻抗
是 和 的比值。参考公式浅掺杂发射极 BJT 紧凑模型基极电流计算式 输出阻抗
是 和 的比值。 电容由以下指定,
是基极集电极结耗尽区的小信号电容。 是基极发射极结耗尽区的小信号电容。 称为发射极扩散电容。 如果寄生电阻很大,则应在这个理想的小信号模型中添加额外的电阻。
4.2.2. 扩散电容
扩散电容
是基极-发射极正向偏置所引起的所有少数载流子导致的寄生电容。
、 在发射极、基极的少数载流子。 、 基极-发射极、基极-集电极空间电荷区的少数载流子。 每当晶体管内多余电荷重新排列时,
都会引起端电压的变化。为了电路建模的目的,我们经常写,
发射极延迟时间; 基极渡越时间; 基极发射极耗尽区渡越时间; 基极集电极耗尽区渡越时间。 我们定义一个前向渡越时间
为, 在低
时, 与 无关。 在高
下,由于基极电导率调制效应, 不是恒定的。 4.2.3. 少数载流子电荷分布
npn BJT 用于放大时的少子分布。
指向原始笔记的链接当输入电流改变的时候,少子分布也会改变。
2.11. 扩散电容
4.2.2. 扩散电容
扩散电容
是基极-发射极正向偏置所引起的所有少数载流子导致的寄生电容。
、 在发射极、基极的少数载流子。 、 基极-发射极、基极-集电极空间电荷区的少数载流子。 每当晶体管内多余电荷重新排列时,
都会引起端电压的变化。为了电路建模的目的,我们经常写,
发射极延迟时间; 基极渡越时间; 基极发射极耗尽区渡越时间; 基极集电极耗尽区渡越时间。 我们定义一个前向渡越时间
为, 在低
时, 与 无关。 在高
指向原始笔记的链接下,由于基极电导率调制效应, 不是恒定的。
2.12. BJT 截止频率和最大频率
4.3. BJT 的瞬态和交流响应
BJT 的瞬态和交流特性由器件中存储的少数电荷决定。当端电压改变时,存储的少数电荷必须做出响应而改变,并且为此需要时间。
BJT 的高频性能的主要品质因数 (FOM):
- 截止频率,
- 最大振荡频率,
4.3.1. 截止频率
2021 #EE6604期末/2022 #EE6604期末/2023
定义为发射极和集电极短路时(
),共发射极小信号电流增益降至单位 1 时的渡越频率。因此,它也称为单位电流增益频率。 描述晶体管用作放大器时的最大有用频率,超出截止频率后 BJT 不在有放大作用。
有集电极电流和基极电流,
与频率相关的共发射极电流增益:
可以证明,
,因此在高频下, 如果想要增大截止频率,就需要减小结电容,由其是扩散电容。所以扩散电容会减小 BJT 的截止频率。
再代入结电容,
这也是用于计算前向渡越时间的常用公式。前向渡越时间计算公式
指向原始笔记的链接
根据上面这个公式可以画出以
为横坐标, 为纵坐标的图。虚线延长线即交于 。 Question
为什么小
的时候,会有偏差? 是基极电导率调制效应引起的(可以结合古梅尔图来看)。 4.3.2. 最大振荡频率
这是晶体管的最大资用功率增益降至 1 时的频率。
通常大于 ,因为它考虑了电压增益。 这里说明了最大振荡频率为什么会比截止频率高。
在高频的时候,有
, [! note] 这里可以看出,当扩散电容越大,
越大,电压增益越小。 4.3.3.
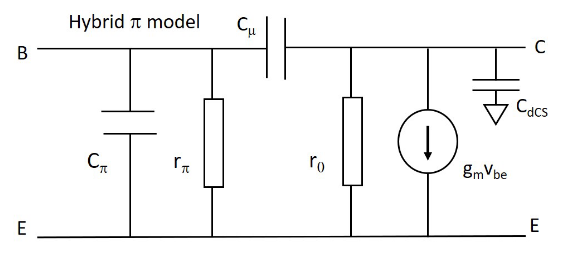
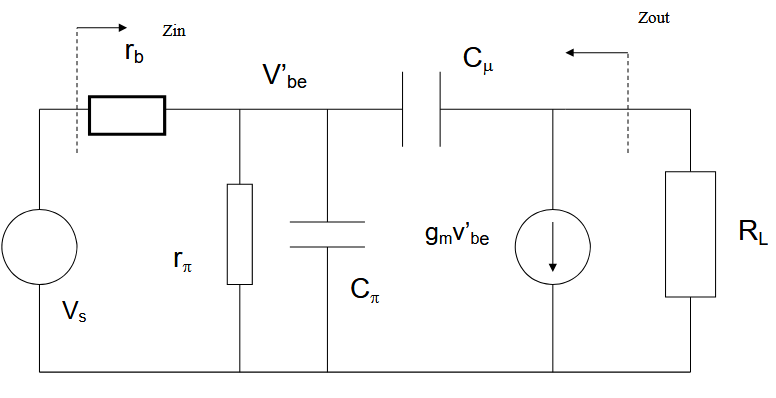
的高频等效电路
这个电路引入了
指向原始笔记的链接和 。
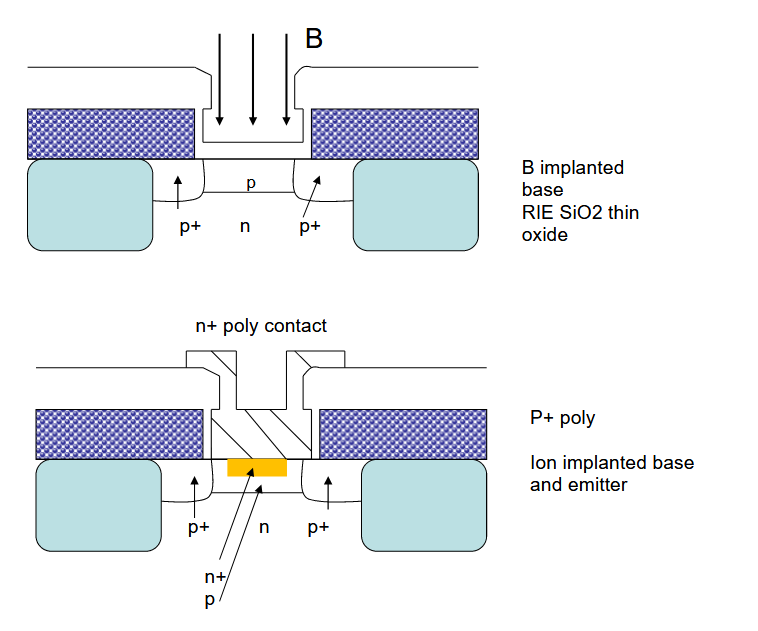
2.13. 双多晶硅自校准发射极 CVD 流程
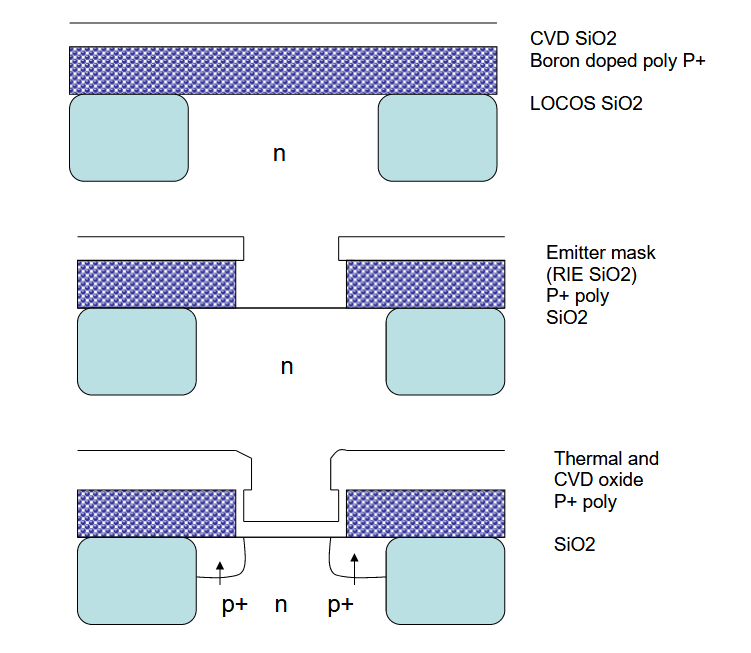
5.3.5. 双多晶硅自校准发射极 CVD 流程
- 原位沉积掺杂 p+ 多晶硅(多晶硅 1)和二氧化硅(原位:沉积和掺杂)
- 使用选择性蚀刻(未蚀刻基板)进行反应离子蚀刻氧化物和多晶硅 1
- 在蚀刻上方生长热氧化物结构; 100-400nm 多晶硅侧壁
- 硼从 p+ 多晶硅扩散形成外基极(和 3 同时发生)
- 用硼植入内基(自对准非本征和本征基极)
- 清洁发射极接触窗 (HF/H2O)
- 沉积多晶硅 (poly2) 并注入砷
- 通过砷掺杂剂的外扩散形成浅发射极(
)。 可以发现,用于接触的第二层多晶硅比发射极更宽。
指向原始笔记的链接
3. 硅 MOSFET
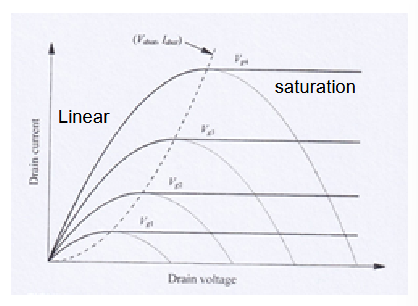
3.1. MOSFET 工作区
4.4. MOSFET 导通时的两个区域
区域的划分是按照
和 的关系来划分的。
- 线性区:电流 Ids 随 Vds 近似线性增加
- 饱和区:电流 Ids 变得与 Vds 无关。
4.4.1. 线性区
栅极电压高于阈值电压;反型层从源极延伸到漏极。
漏极电流,
阈值电压
晶体管的行为类似于具有薄层电阻率的电阻器:
该薄层电阻率由栅极电压
控制。 4.4.1.1. 阈值电压的实验测定
绘制小 Vds 情况下的 Ids 与 Vg 的关系图。将 Ids (Vg) 曲线的线性部分外推到 Vg 轴并找到 Vg 截距。注意:这个线性外推的阈值电压并不完全是 Vt,通常指定为
。 4.4.2. 饱和区
m 通常在 1.1-1.4 范围内。
最大电流出现在
处, 此时有电流,
4.4.3. 夹断
指向原始笔记的链接
3.2. PMOSC 偏置状态
1.4.2. 偏置情况
根据栅极电压,MOS 电容能被偏置到以下四种平衡状态,
- 平带
- 累积
- 耗尽
- 反型 这里我们只关注 p-MOS 电容的耗尽和反型阶段。
1.4.2.1. 平带
上面图是栅极、氧化层和 p 衬底的能带图。对于 MOS 电容而言,这是一种特殊情况,在硅内没有净电荷或者电场。并且只在特殊的栅电压下出现。
Note
硅和氧化物的能带都是平坦的。对于假设的
的情况,平带会发生在平带电压 (但是通常来说, 都不为 0) 1.4.2.2. 积累层形成
当对栅极施加负电压的时候,栅极的总电势会低于 p 衬底的电势,由此在氧化层中形成了一个从 p 衬底指向栅极的电场。电场的存在改变了衬底表面的电势分布,使得衬底表面附近的电势能增加,从而使得价带顶和导带底的能级上升。导带底的能级上升,使得表面附近的电子能态能量增加。价带顶的能级上升,使得表面附近的空穴能态能量降低。由于价带顶的能级上升,价带中的能态能量更接近费米能级(平衡状态时,
在整个衬底中都是恒定的),根据费米-狄拉克分布函数,更多的空穴会被吸引到表面附近,导致空穴浓度增加。 或者直观来看,栅极施加负电压,栅极电子累积导致衬底空穴累积,才能形成电容。
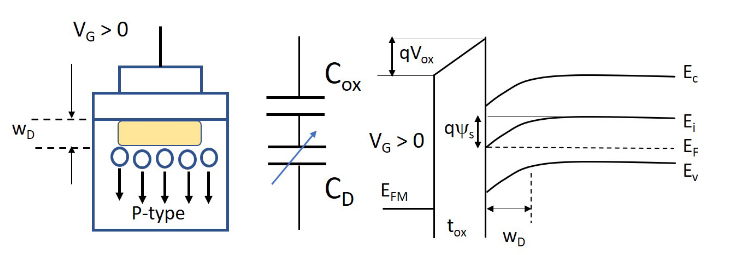
1.4.2.3. 耗尽层形成
当对栅极施加正电压的时候,栅极的电势会高于衬底的电势,由此在氧化层中形成一个从栅极指向衬底的电势。电场的存在使得衬底表面电势能下降,价带顶和导带底能级下降。从而使得电子能态能量减少,空穴能态能量增加。由于导带底的能级下降,使得导带中能态能量更接近费米能级,从而使得电子在导带中出现概率增加,电子浓度上升。
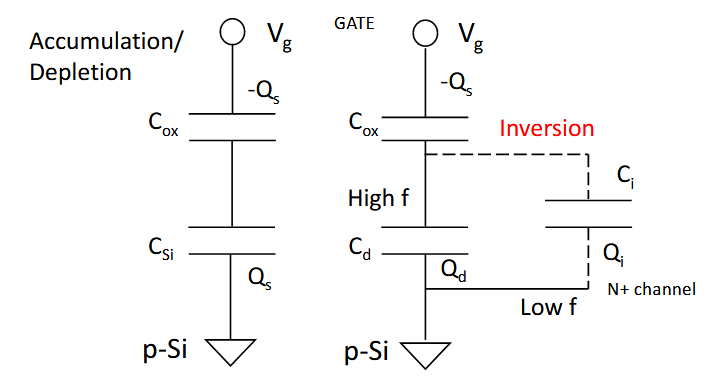
可以看到,此时的电容由氧化层电容和耗尽层电容两个部分串联组成。
上面的能带图是一个特殊情况,即
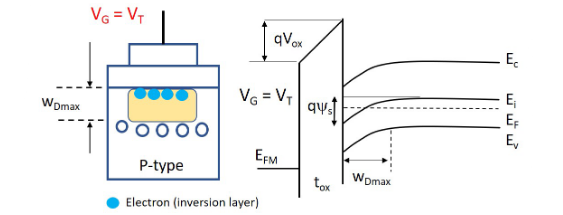
的时刻,此时是反型层恰好开始形成。 1.4.2.4. 反型层形成
相对于硅衬底的正栅极偏压。金属中电子的能量相对于硅来说较低。在氧化硅中感应出电场。 Si 的能带向下弯曲; Si 表面附近的空穴浓度降低。 Si 表面耗尽了多数载流子,耗尽宽度为 WD。
此时有
,说明基底已经从 P 型反型为 N 型。 反型又分为弱反型和强反型,
- 弱反型:一旦表面上的
与 重合(即 MOSFET 关闭),就会发生。 - 强反型:当表面的电子浓度等于 Si 本体中的空穴浓度时(⇒ MOSFET 导通),就会发生这种情况。
在强反转时,Si 中的负电荷由以下部分组成:
指向原始笔记的链接
- 表面反转层中的电子(移动)
- 负受主掺杂剂固定电荷(静止) 由于反型层的静电屏蔽效应,耗尽层的宽度不再随栅极偏压而增加。此时耗尽层的最大宽度为
。
3.3. 表面电势和电荷密度的关系
![[《Chapter 2 硅 MOSFET 》笔记#144-硅电荷-q_s|1.4.4. 硅电荷
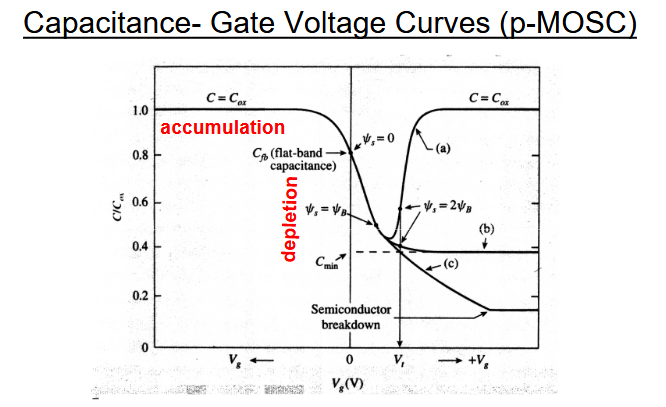
3.4. MOSC 的 C-V 关系
1.4.6. 电容-电压关系
2021 #EE6604期末/2022
1.4.6.1. 电容-电压:积累
由泊松方程的解可知,在累加区:
对 Qs 对
求微分: MOS 电容为,
由于室温下为 2kT/q ~ 52mV,第二项很快变得可以忽略不计,随着 Vg 减小,MOS 电容 C 迅速接近 Cox。对于逐渐减小到接近
的电压,电容会减小。 1.4.6.2. 电容-电压:耗尽
在这个区域,耗尽近似适用并且
其中 Cd 是耗尽区电容。总电容为,
电容随着该区域栅极偏压的增加而减小。
1.4.6.3. 电容-电压:反型低频(a)
电容取决于小信号电压的频率。对于准静态(低频)情况,一旦达到
就会形成反型层。 受反型电荷随 变化的影响。电容迅速增加回到 Cox。这是因为热激发有时间产生电子来调制反型层中的电荷。 1.4.6.4. 电容-电压:反型高频(b)
如果施加的交流信号的频率太高,反型电荷(少数载流子)将无法跟随信号变化,只有耗尽电荷(多数载流子)可以响应。
由耗尽宽度为最大值 的耗尽电容给出。高频电容是一个常数: 如果其频率低于少数载流子响应时间的倒数,则反转电荷只能跟随交流信号。该响应时间与少数载流子寿命成正比,通常为 0.1-10 秒,具体取决于晶圆质量(缺陷)。通常,对于高于 ~100Hz 的频率,只能观察到高频电容。
1.4.6.5. MOS 电容等效电路
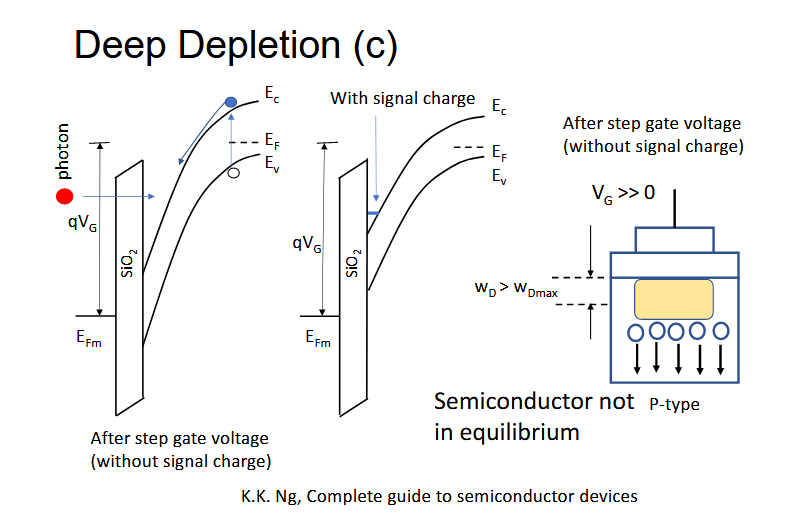
1.4.6.6. 深耗尽(c)
指向原始笔记的链接
3.5. 亚阈值电流机理
4.5.1. 亚阈值电流机理
亚阈值电流产生的本质是在 MOSFET 处于弱反型时,电子能通过热发射越过势垒。
在亚阈值区域,扩散电流和漂移电流都很重要。这与漂移电流是主要电流分量的饱和区不同。分析亚阈值电流并不容易,我们仅限于低漏极偏置的情况。将反型电荷 Qi 代入漏极电流方程并积分可得出:
[! note] 注:亚阈值电流取决于 Vg、Vds 和体效应系数。然而,对于大于几个 kTs 的 Vds,亚阈值电流主要由 Vg 控制。
3.6. 亚阈值斜率
4.5.2. 亚阈值斜率
2022 #EE6604期末/2023
亚阈值摆幅用来描述 mosfet 在亚阈值区域的电流-电压特性。其定义为在亚阈值区域内,栅极变化 1V,漏极电流的对数值变化量。可以用来衡量多快能将
降到 之下。 亚阈值摆幅计算式
指向原始笔记的链接 ,并注意 。通常, 。S 越小,器件关断越快。 [! note] 注意:由于导出 Ids 时采用了近似值,上面给出的 S 表达式低估了实际亚阈值斜率 5-10%
[! note] 亚阈值斜率 S 主要由热载流子的玻尔兹曼分布决定(见亚阈值电流的机理),而这种分布与MOSFET的物理尺寸无关。因此,即使MOSFET的尺寸缩小,热载流子的分布特性仍然保持不变
对于 VLSI 应用,S 应较小,以获得快速器件关断。然而,这并不容易实现,因为 S 主要取决于温度 T。可以利用衬底掺杂剂浓度 Na 和栅极氧化物厚度通过体效应系数将 S 调整到有限的程度。
4.5.2.1. 亚阈值斜率的重要性
亚阈值斜率对于低功率微电子学尤其重要。通常,降低电源电压以节省待机功率和开关功率。然而,由于 S 的有限值和可扩展性有限,电源电压不能任意小。降低 Vcc 过多可能会导致逻辑“0”处出现显着漏电流,因为逻辑低电平与 Vt 太“接近”。
指向原始笔记的链接
3.7. 短沟道效应
5.1.2. 短沟道效应
2021 #EE6604期末/2022 #EE6604期末/2023
短沟道效应是指随着沟道长度减小,MOSFET 阈值电压
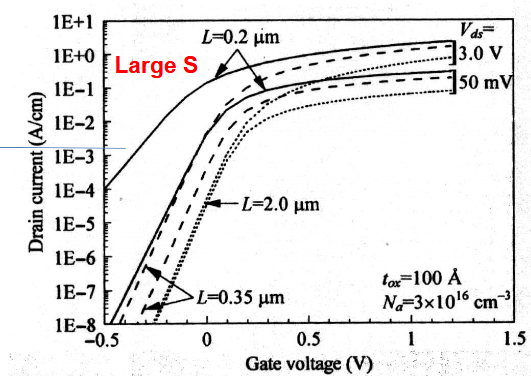
幅度的减小。对器件施加漏极偏置 可能会使 SCE 变得更糟。从下图可以看到,当随着沟道长度减小到一定程度的时候,阈值电压的幅度也在减小。 SCE 的后果:
- 可能导致器件漏电流和功耗增加。
- 芯片上的最小几何器件必须根据 SCE 进行设计。
短沟道 MOSFET 中的亚阈值电流,可以看出当 L 减小到 0.2
,栅极电压的减小无法将 MOS 完全关闭。 5.1.2.1. 短沟道效应的物理原因
对于长沟道器件,模拟2μm 器件主要沿 y 轴的等势(平行于 Si-SiO2 界面)。电场仅在 x 方向上变化。 y 方向的变化最小。*一维场模式。
这里可以看出,沿着沟道的电子电势基本是和沟道长度相当且平稳的(仅仅在接近源端和漏端处呈现二维电场)。
对于短沟道器件,对于相同的 Vg 和 Vds,等电位线更呈曲线状。电场是二维的。 Si 表面的能带弯曲更大,耗尽区更宽。器件具有较低的阈值电压。
二维场图案是由于源极和漏极靠近而产生的。每个形成一个 p-n 结并具有相关的耗尽区。对于长沟道情况,这些耗尽区相距足够远,不会影响器件中的场图案。对于短沟道情况,源极-漏极的间隔与 MOS 耗尽宽度相当,因此场图案受源极漏极电压的强烈影响。
5.1.2.2. SCE 导致的阈值电压下降
用来解释这个现象的主要有两个模型:
- 电荷分享模型
- 漏极诱导势垒降低(DIBL) 我们主要看第二个模型。
该图显示了表面电势(对于电子)作为归一化距离 y/L 的函数。在源极 (y/L=0) 处,当器件关闭时,表面势垒可防止电子进入沟道区域。对于长沟道情况(曲线 A),大部分沟道上的势垒是平坦且均匀的。对于短沟道情况(曲线 B、C),势垒较低且更圆。如果漏极偏压增加,势垒会进一步降低 (DIBL)。降低的势垒增加了电子进入通道的可能性并导致阈值电压降低。
具有均匀掺杂密度的 nMOSFET 耗尽区的电场由下式给出:
注:
可以解释为由栅极场控制的电荷密度, 为由源漏场控制的电荷密度 模拟横向场与耗尽区距离 y 的关系
指向原始笔记的链接注:对于 (a),横向场随距离呈指数减小。这种指数衰减的特征长度不随沟道长度而改变。因此,短沟道器件中间的横向场强于长沟道器件。施加漏极偏压将零场点移向源极。零场点对应于 DIBL 中的潜在最大值点。
3.8. 源极漏极拓展
5.2.1. 源极漏极扩展
2021 #EE6604期末/2023
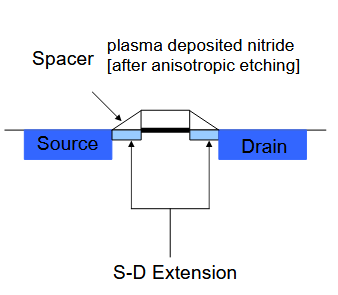
浅结插入源极-漏极和亚微米器件通道之间。自对准离子注入形成 S-D 延伸(低剂量)。沉积隔离介质 (SiN),然后进行第二次高剂量自对准注入。保持源极-漏极从通道“凹进”。权衡是寄生源漏串联电阻的净增加。
5.2.1.1. 源漏串联电阻
寄生电阻与源极和漏极区域以及欧姆接触的有限薄层电阻率相关。这种外在效应在长沟道器件中并不重要,因为长沟道器件的沟道电阻相当大,可以忽略不计。然而,沟道电阻与亚微米器件中的源极漏极电阻相当。因此,这种外在效应现在很重要。
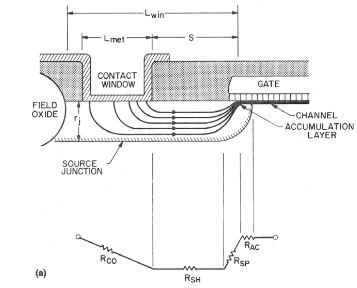
寄生源极漏极电阻可分为四个部分:
- Rac:积累层电阻
- Rsp:扩散电阻
- Rsh:薄层电阻
- Rco:接触电阻 由于栅极驱动的减少,源极侧电阻尤其不受欢迎。
累积层电阻栅极边缘通常与源极和漏极重叠。在栅极-源极(或-漏极)重叠区域,载流子被限制在具有电阻 Rac 的累积层中。
扩散电阻这是与注入电流从薄累积层扩散到源极或漏极相关的电阻分量。对于均匀掺杂的源极-漏极,
其中 是电阻率; xj 和 xc 分别是结深度和累积层厚度。 W 是器件宽度。 薄层电阻这是源极-漏极扩散区域的电阻,可以简单地由下式给出,
其中 S 是栅极边缘和金属接触边缘之间的间距,
是源漏扩散的薄层电阻率。由于 值较低,该电阻分量通常可以忽略不计。 接触电阻由下式给出:
其中
指向原始笔记的链接是接触窗口的宽度; 是金属和硅之间欧姆接触的界面接触电阻率。单位为欧姆-cm2。欧姆接触中的电流主要由隧道效应或场发射决定。因此, 强烈依赖于势垒高度和表面掺杂浓度。
4. 异质结
4.1. 维加德定理
1.1.1. 维加德定律 Vegard’s Law
维加德定律是指对于三元化合物
(其中 A 和 B 是同族元素(III 族或 V 族元素)),参数 P 可以表示为带隙 Eg 或晶格常数(LC), 其中 X 是摩尔分数或组成,可以在 0 到 1 之间变化。
1.1.1.1. 晶格常数
从这张图就可以看出,用不同或者相同晶格常数的元素进行替换的时候,合金晶格常数是如何变化的。
1.1.1.2. 能带间隙
三元和四元半导体的带隙仅大致遵循维加德定律。
在大多数合金中,由于不同元素的合金化而导致无序性增加,从而产生弯曲效应。合金半导体的能带隙可以用以下表达式更好地描述:
从一次关系变为了二次关系。
指向原始笔记的链接
4.2. 临界厚度
1.2.3. 临界厚度
存在一个临界厚度
,低于该厚度生长的薄膜会发生应变,而不会出现失配位错(赝晶生长),在此之上,薄膜变得不受应变或松弛。与界面处失配位错的形成相关,临界厚度为, 指向原始笔记的链接
对于大多数(100)半导体系统( 是衬底的晶格常数); 是泊松比,近似值为 0.274; 是晶格失配。
4.3. 异质结和同质结的对比
2.4. HBT 与同质结的对比
2021 #EE6604期末/2022
从 BJT 的共发射极增益再进一步推导,能看到
和发射极与基极之间的带隙差有关。 这意味着可以对基极进行大量掺杂并实现低基极电阻。还可以将基极做得更窄,以实现高速。因此,我们对高性能晶体管的所有要求都可以通过具有更大带隙发射极来满足。
指向原始笔记的链接
4.4. 异质结基本结构
2.5.1. GaAs/AlGaAs HBT
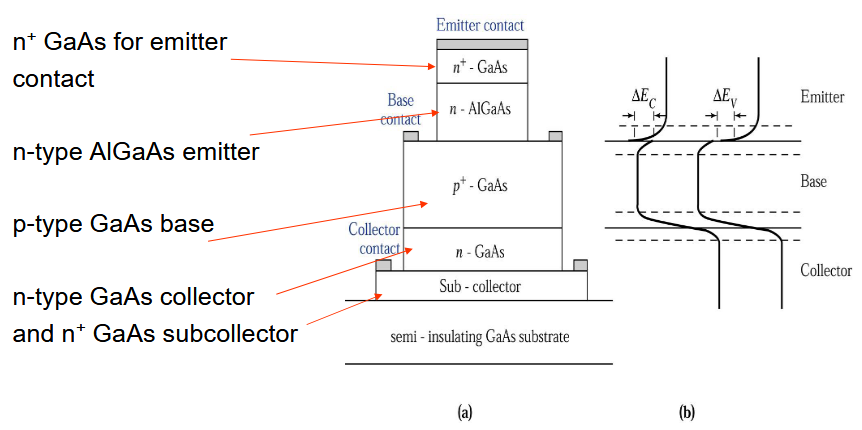
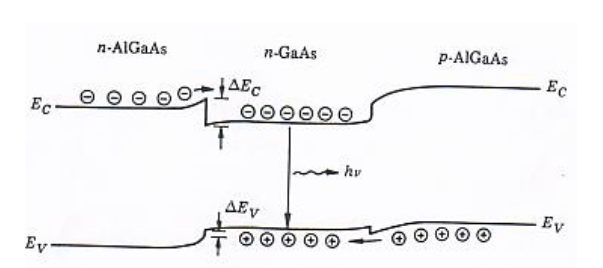
这个是一个基本的 HBT 结构,发射极由宽禁带的
指向原始笔记的链接构成,基极则是由宽度较窄的 p 掺杂 构成,集电极则是 n 掺杂的 。
4.5. HBT 发射极、基极集电极改进
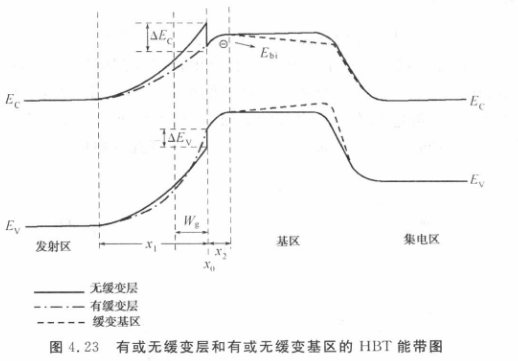
2.6. 进一步提高 HBT 性能的途径
2021 #EE6604期末/2022
2.6.1. 发射极
在发射极主要关注上图中的导带不连续,这会导致电子需要通过热发射或者隧穿才能到达基极,从而导致发射极效率降低或者集电极电流减小。
这个问题可以通过使用改进的结构来缓解,例如在 E-B 结附近使用具有渐变层的发射极。
2.6.2. 基极
基区也可采用缓变分布, 使得基区的带隙由发射极一侧到集电极一侧逐步减小。存在一内建电场
准中性基区 (quasi-neutral base) ,少数载流子渡越时间降低, 增加了 HBT 的共发射极电流增益与截止频率。 2.6.3. 集电极
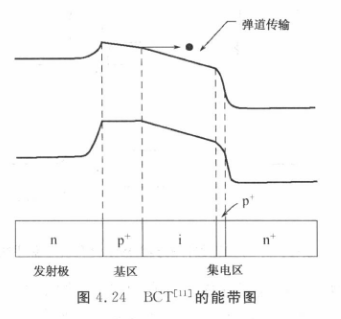
集电极我们主要考虑的是 集电区渡越时间和 击穿电压。采用特定的集电区掺杂,例如具有
集电区和一层临近次集电极的 脉冲掺杂结构(pulse-doped)的 HBT。这样在维持集电区厚度的同时,能使得电子在大部分渡越时间内,可以维持导带低能谷的高迁移率(参考 Ridley-Watkins-Hilsun 机制),这种器件叫弹道集电区晶体管。 指向原始笔记的链接
4.6. MODFET 能带分析
3.2. 能带分析
能带图中,
为金属和宽带隙半导体的势垒高度,MODFET 的内建电势为,
为 的施主掺杂浓度; 为 的掺杂区厚度; 为介电常数。 MODFET 的关键工作参数为阈值电压
,对应的状态是 表面的导带底与费米能级重叠(见图(b))。 当 MODFET 开启的时候,栅极在异质界面处容性感应出电荷薄层
,类似与 MOSFET 的沟道电荷。 指向原始笔记的链接
5. 光电器件
5.1. 分布反转
1.2.1. 分布反转
为了增强激光操作的受激发射,分布反转是必要的。这可以通过在结的两侧进行非常重的掺杂来实现,能使得 p 型区的费米能级低于价带顶,而 n 型区的费米能级能高于导带底。
上图左边是同质结激光和双异质结(double-heterojunction,DH)激光的结构以及正向偏压下的能带图。
当施加足够大正偏置电压的时候就会发生大注入,在过渡区会有大量集中在导带中的电子和价带中的空穴。这里也能看出异质结的优势,能构建更高的势垒,使得载流子累积浓度更大。而在同质结激光器中,载流子可以离开发生辐射性复合的有源区。
分布反转所必需的条件为
指向原始笔记的链接,也就是结两侧费米能级差大于带隙。
5.2. 光学约束
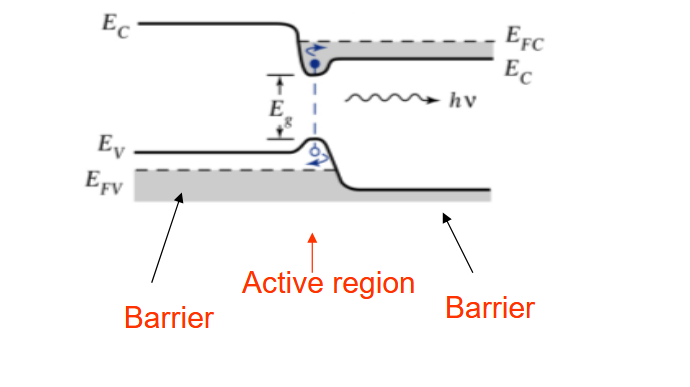
1.2.2. 载流子与光学约束
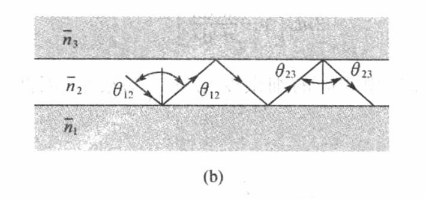
载流子都被限制在有源区(两端都有异质结势垒)。因为
有更大的折射率,当入射角度大于临界角的时候,就能发生全反射,由此能将光子同样束缚在有源区。
定义一个约束因子
,它是有源层内的光强度与有源区域内外的光强度之和的比率。 约束因子计算式
指向原始笔记的链接
是常数; 是折射率差; 是有源区的厚度。 可以看出,当折射率差越大、有源区厚度越大,约束因子就越大。
指向原始笔记的链接
5.3. 光学腔与光学增益
1.2.3. 光学腔与反馈
光学腔本质就是一个谐振腔,使得光子在其中多次传播,以获得更高的光增益。对于半导体激光器,应用最广泛的腔是法布里-珀罗腔。
法布里-珀罗腔
法布里-珀罗腔结构是一种典型的激光器结构。在结的左右制造镜面,在结的前后粗糙化。一般制造镜面的方式有使用晶体的劈裂面。激光从镜面处射出。
每个镜面的反射率
为, 介质界面反射率计算式
指向原始笔记的链接
为波长为 时半导体的折射率。 谐振模式是指腔内光的半波长的整数倍等于腔长度的模式,增强且相干的光会在激光腔中来回地反射。对于一个长度为
的腔有, 其中 m 是整数,L 是腔长,n 是腔的折射率,
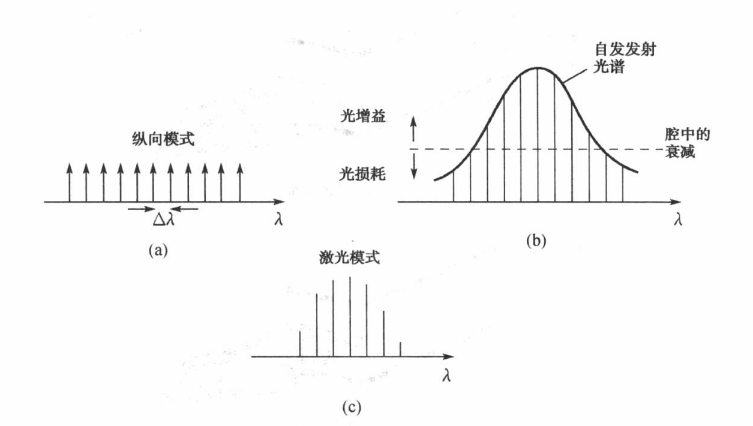
是光波长 光的波长实际上是被带隙所控制的。许多
值都可以满足共振条件,但只会产生自发发射光谱内的值。并且由于光损耗,只有最强的谱线才能被保留。最后能产生的谱线的集合就是激光模式,也叫作纵向模式。
纵向容许模式的波长间距
对应于 和 个模式之间的波长差,对 求导可以有, 然
是 的函数,但是波长在临近模式之间的细微变化量 的变化非常小,由此在 的条件下,近似的有, 指向原始笔记的链接
5.4. DH 激光器波长计算
1.3. 双异质结激光器
有一层很薄的
被另外一种半导体层( )包夹。 [! attention] 下面的阈值电流密度在不同书里面给出的公式也不一样,这里按照 [1]P. Z. Qing, “2. Heterojunction photonic devices,” Oct. 2024. 的内容来。
阈值电流密度
是激光器工作的最重要的参数之一,是产生激光所需的最小电流密度。温度越高,阈值电流密度越高。将激光器建模为一个二极管和串联的电阻 。施加的电压为 。
有电流为,
当激光器开始工作之后,在二极管上的压降恒定为
,此时有电流, 阈值电流密度为,
阈值电流密度计算式
指向原始笔记的链接
为增益因子; 是吸收或其他散射机制引起的每单位长度的损耗; 是光学腔长度; 是光学腔一端反射镜的反射率。 例题很简单,最后要求的是激光的波长,
光子波长计算式
指向原始笔记的链接
为光速; 为光子频率; 为普朗克常数; 为元电荷; 为电压。 根据普朗克关系式有,
普朗克关系式
指向原始笔记的链接 根据电流算出带隙即可。
阈值电流和温度的关系,
指向原始笔记的链接
5.5. 暗电流
2.3.2. 暗电流和光电流
2021 #EE6604期末/2022
当仅仅施加偏压而没有入射光的时候,光电探测器仍然有电流存在,叫作暗电流。暗电流
主要由隧穿电流 和热发射电流 构成。 暗电流是越小越好。 光电流则是由于吸收入射电子而从基态跃迁到激发态,
为光激发电子浓度; 为迁移率; 为电场。 前面说了 QWIP 对红外的吸收是通过导带内或者价带内的量子阱实现的,具体有三种跃迁方式。我们主要看第一种。在偏置状态下,电子从量子阱束缚态跃迁到下一个量子阱束缚态。在每个量子阱里面,都束缚有量子化能态,当电子从基态被光子激发到第一束缚态后,就能通过隧穿出阱,然后进入下一个阱中。
当 QWIP 被照射的时候,总电流是光电流和暗电流的和,但主要是光电流,
指向原始笔记的链接
6. 存储器件
6.1. CMOS 锁存
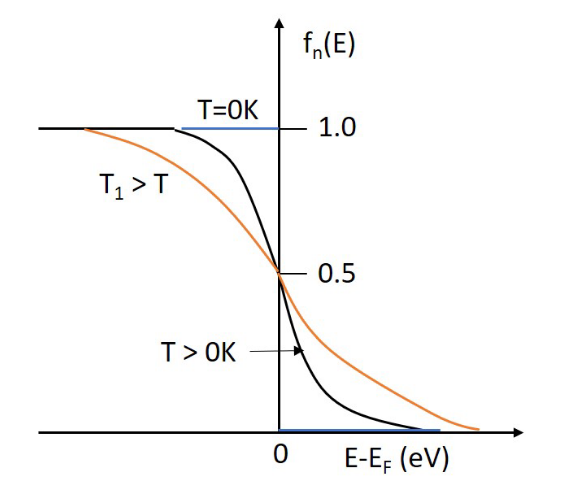
2.2.2. 六晶体管 (Six-T) 单元
6-T 单元在锁存器的基础上,加上了
和 来控制,这两个晶体管称为存取晶体管(access transistors)或传输晶体管(pass transistors)。他们的功能有,1. 将单元与其他单元隔,2. 提供从存储单元写入和读取信息的路径。 2.2.2.1. 常用的 SRAM 存储单元
两个耗尽型 NMOS 和四个增强型 NMOS 构成;
有多晶硅负载电阻的NMOS 存储单元。
6-T CMOS 存储单元(主要使用)。 CMOS 存储单元与其他存储单元相比的优点:
- 功耗小
- 体积小
- 漏电流小
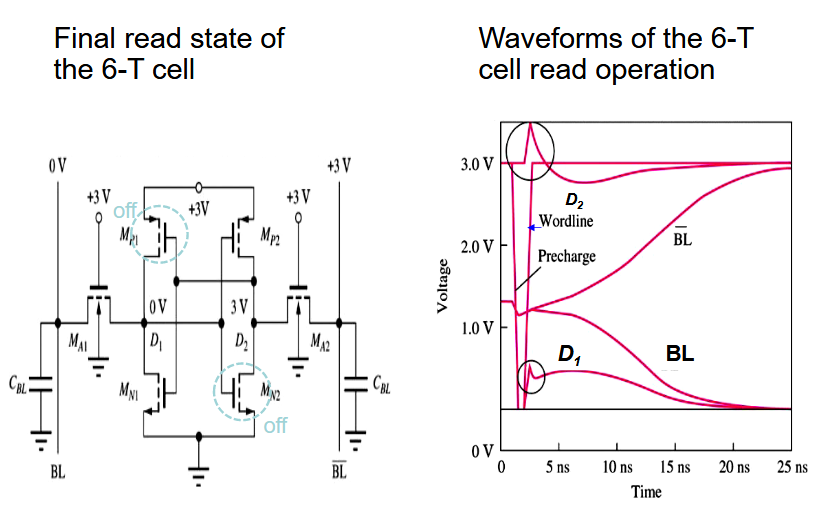
2.2.2.2. 6-T 单元的读 0 操作
假设有
、 ,并且 。 首先将位线预充电到 ,随后将字线电压提升到 开启两个存储晶体管。晶体管开启之后,可以通过对 、 还有 的分析得出两个存取晶体管的状态, 工作在线性区, 工作在饱和区。预充电的位线电容器通过存取晶体管承载分别流经 和 的工作电流 和 。 电压将因 电容器放电而下降,而 电压将因电容器充电而升高, 从而完成读取 0。 由于电流 i1 和 i2 造成的 D1 和 D2 节点电压的任何干扰都可以通过锁存操作快速校正,并且存储在单元中的原始数据得以保留。可以看下面的波形图进行理解,这也是为什么位线要预充电到
,用来减小电流波动。
2.2.2.3. 6-T 单元的读 1 操作
读“1”操作遵循与之前相同的概念,只是交换了存取晶体管的源极和漏极(电位较低的端子为源极)。请注意,此特定单元有大约 20 ns 的延迟。
2.2.2.4. 例题
Calculate
and in the READ ‘0’ if all devices have . Assume , , , and . Solution
一点复习,免得忘了:
对应的管子是 ,所以 , , ,在线性区 代入线性区电流公式 注意这里的单位取决于工艺跨导参数的单位(
)
对应的管子是 ,所以 , , ,在饱和区 代入饱和区电流公式 指向原始笔记的链接
6.2. DRAM 写入时初始电流
2.3.2. 写数据
2.3.2.1. 存 “0”
- 将位线设为 0V
- 将字线设为 3V
如果 C 原本就是 0V,则无变化。如果原本是存储了“1”,则会形成电流。
假设
, , 2.3.2.2. 存“1”
- 将位线设为 3V
- 将字线设为 3V
如果原本是“1”则无变化,如果原本是“0”,则有流向电容的电流。
阈值电压计算式
指向原始笔记的链接
为零偏置阈值电压; 为体效应系数; 为阈值表面电压; 为源衬电势差。 长沟道 MOS 器件线性区漏极电流计算式
指向原始笔记的链接
为工艺跨导参数 NMOS 饱和区的漏极电流计算式
指向原始笔记的链接
为沟道长度调制系数。
6.3. DRAM 读取时电压差
2.3.3. 读数据
2022 #EE6604期末/2023
- 位线预充电至大约 VDD/2 或 VC/2。
- 通过将 WL 升高至 3V (VDD) 打开 MA
2.3.3.1. 电荷共享模型
(a) 访问晶体管激活之前的电路模型 (b) 访问开关闭合之后的电路。
MA 开启前的初始总电量,
MA 开启并稳定之后,
假设没有电荷损失,
,能得到位线电容上的电压为, 要检测的信号是位线相对于其初始预充电值的变化:
如果假设
,则有 BL 和其电容器上的最终电压由下式给出, 这意味着 VBL 和 VF 这两个电压之间的差异非常小,但仍然可以被读出放大器测量,从而可以识别存储的逻辑电平。
2.3.3.2. 充电时间常数
除了理想开关的情况外,电荷转移不可能瞬时发生。电路中的电压和电流将随时间常数
呈指数变化,由下式给出, 充电时间常数计算式
指向原始笔记的链接
为存取晶体管的导通电阻; 为位线电容; 为存储电容的电容值,有
6.4. 放电率
2.4.2.1. 1-T 单元的放电率
放电率(discharge rate)的定义为,
指向原始笔记的链接
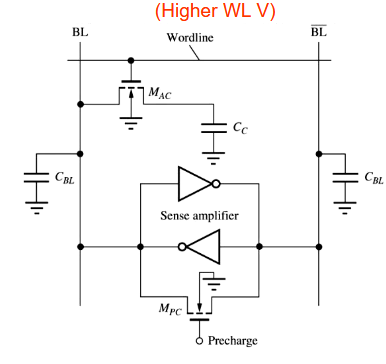
6.5. 升压字线电路
2.5. 升压字线电路
高速度意味着快速访问,需要高放电倍率。高放电倍率需要高充放电电流。这可以通过采用被称为升压字线的高字线电压来实现。
高速度意味着快速访问,需要高放电倍率。高放电倍率需要高充放电电流。这可以通过采用被称为升压字线的高字线电压来实现。
指向原始笔记的链接
6.6. EPROMs
2.6.5. EPROMs
有可多次编程的可擦除可编程只读存储器 (EPROM) 单元。这种 EPROM 单元仅包含一个存储晶体管,该晶体管通常保存多余的电荷。要重新编程 ROM,必须擦除旧数据。这可以通过从正在使用的系统中取出芯片并将其置于特殊的紫外线源下进行擦除来完成。
浮栅 EPROM 单元
(a) 基本叠栅 EPROM 晶体管。(b) 具有等效控制电容和浮栅电容的电路符号。
- 栅极 C - 控制栅极
- 栅极 F - 浮栅
- CC - 控制栅极电容
- CF – 浮栅电容。
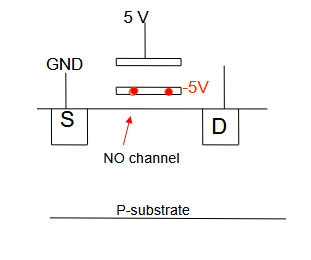
如何编程?假设 EPROM 单元的浮动栅极最初没有电荷。要写入“0”,无需执行任何操作。要写入“1”,EPROM 单元的控制栅极和漏极需要升高到高电压(通常为 12 V)并持续几百微秒,而源极和衬底处于 0 V。
2.6.5.1. 机制
大的漏极电流在其正常传导模式(电子流
)下流过器件。漏极-衬底耗尽区中的高场会导致漏极-衬底结发生雪崩击穿,从而产生额外的电流 ( )。这种高场将电子加速到很高的速度。进入电场约为 105V/cm 或更大的衬底区域的电子将变成“热电子”。 一旦热电子获得足够的能量,它们就可以克服衬底和氧化物绝缘体之间存在的 3.2 eV 能垒(红虚线)。(不会发生隧道效应)穿过薄氧化物的一小部分电子被捕获在浮栅上。由于带负电的电子被捕获,氧化物的能带随后变成固体能带。
假设被捕获的电子会产生大约 –5V 的电位,当 5V 的信号施加到控制栅极时,晶体管中不会形成沟道,这表示单元中存储的是逻辑“1”。
2.6.5.2. 如何擦除
将 EPORM 单元(晶体管)暴露在紫外线辐射下约 20 分钟,即可去除存储在浮栅中的电荷。机理,在紫外光(发射 2537 Å (4.9 eV) 辐射的汞弧灯或蒸气灯)下,入射光子被浮动多晶硅栅极的导带和价带中的电子吸收。从进入氧化物的多晶硅栅极激发的电子被局部场扫至控制栅极或衬底。问题:需要将芯片从使用中的系统中移除,并且所有单元都将被擦除。
指向原始笔记的链接

-Six-T-NMOS-memory-cell..png)