前面的一些应用就略过。

1. 基础知识复习——BJT 和半导体物理

[! summary] 这一部分的内容包括 BJT 基础和半导体物理基础，对于后面了解 BJT 建模和 MOS 建模很重要。

1.1. BJT

[! tldr] 这一部分的内容，最为重要的是对 BJT 的结构以及工作模式有一个感性的认知，能够将电压变化、能带变化和工作模式变化对应起来。

其他内容仅作了解即可。

1.1.1. 点接触 BJT

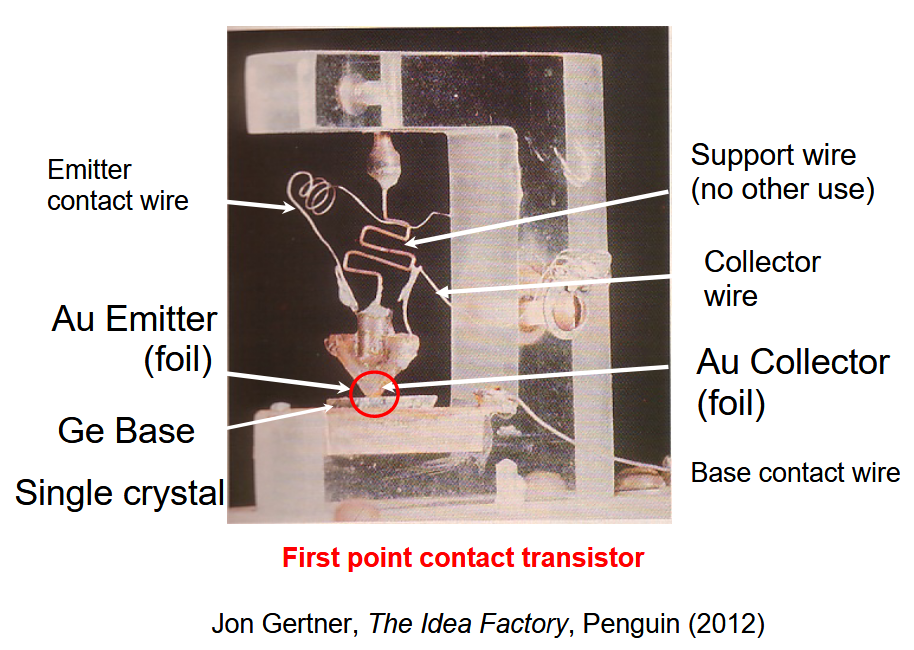
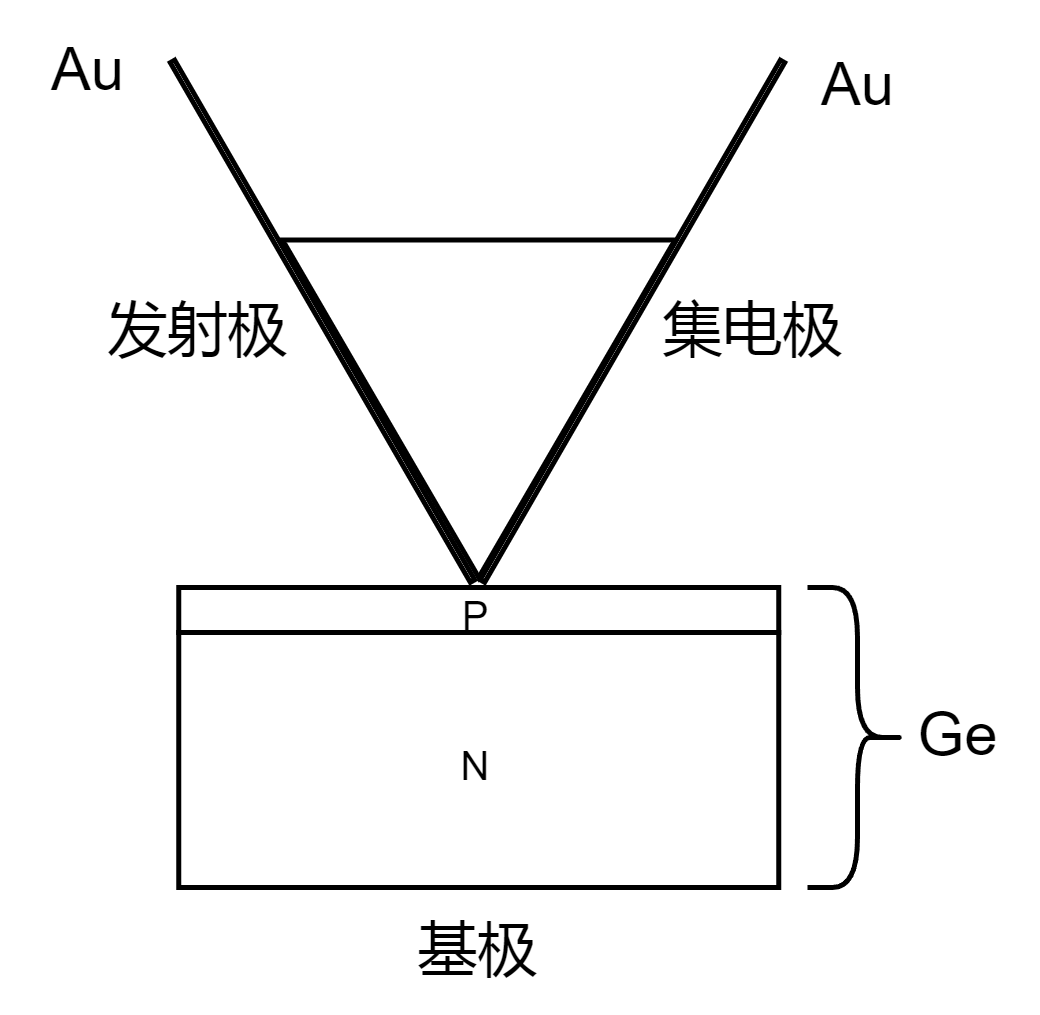
点接触晶体管

点接触晶体管，即上图中红圈位置。它由 n 型锗（）晶体制成，并构成了这个晶体管的基极。

将薄金箔放在“三角形”片上，并用剃刀非常仔细地切割三角形的尖端，使两片金箔彼此非常接近（约 50 微米）。一个称为发射极，另一个称为集电极。支撑线将三角形片压在 Ge 基座上并形成两个“肖特基接触”。一种是正向偏置，另一种是反向偏置。
指向原始笔记的链接

1.1.1.1. 肖特基接触

肖特基接触
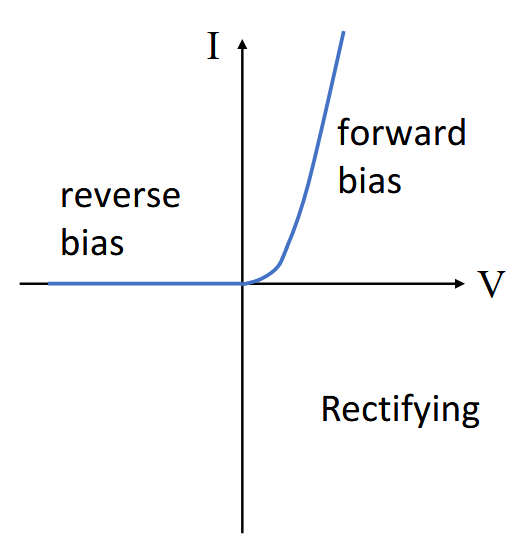
肖特基接触是一种金属-半导体整流接触，一般使用 n 型半导体。

指向原始笔记的链接

1.1.1.2. 欧姆接触

欧姆接触
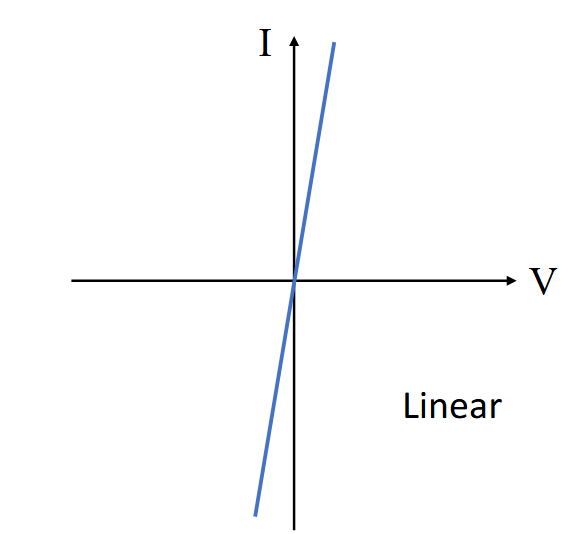
欧姆接触是一种金属-半导体非整流低阻抗结，其可以让两个方向的电流通畅。理想情况下，通过欧姆接触的电流应该是外加电压的线性函数，而且外加电压很小。

势垒类型

常用的欧姆接触的势垒有两种类型，理想无整流效应势垒和隧道效应势垒

特征量

欧姆接触的特征量是接触电阻
指向原始笔记的链接

肖特基接触和欧姆接触的区别在于，肖特基接触的电压电流关系是非线性的，欧姆接触的电压电流关系是线性的。

1.1.2. BJT 结构

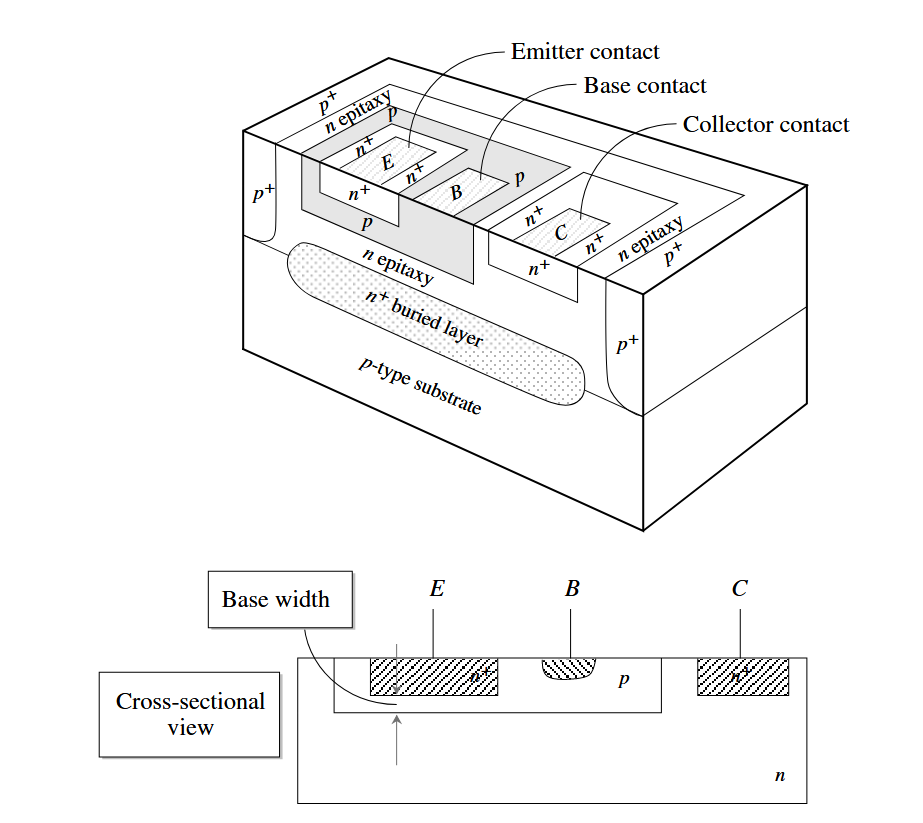
BJT 结构

BJT 可以分为三个不同掺杂的半导体区域，发射极（E）、基极（B）和集电极（C）。

发射极为重掺杂 n 型，p 区形成基极，低掺杂 n 区为集电极。

发射极掺杂远大于基极掺杂，同时也是最小的区域。这样能确保器件具有高电流增益，即小的基极电流变化产生大的集电极电流变化。

基极区位于发射极和集电极之间，由轻掺杂、高电阻率材料制成。基极环绕着发射极区域。

集电极环绕着基极区域，一般为低掺杂区域。一般也会有一个重掺杂的子集电极（sub-collector）用于给集电极提供一个低阻路径（见下图掺杂的集电极区域）
指向原始笔记的链接

1.1.3. BJT 工作模式

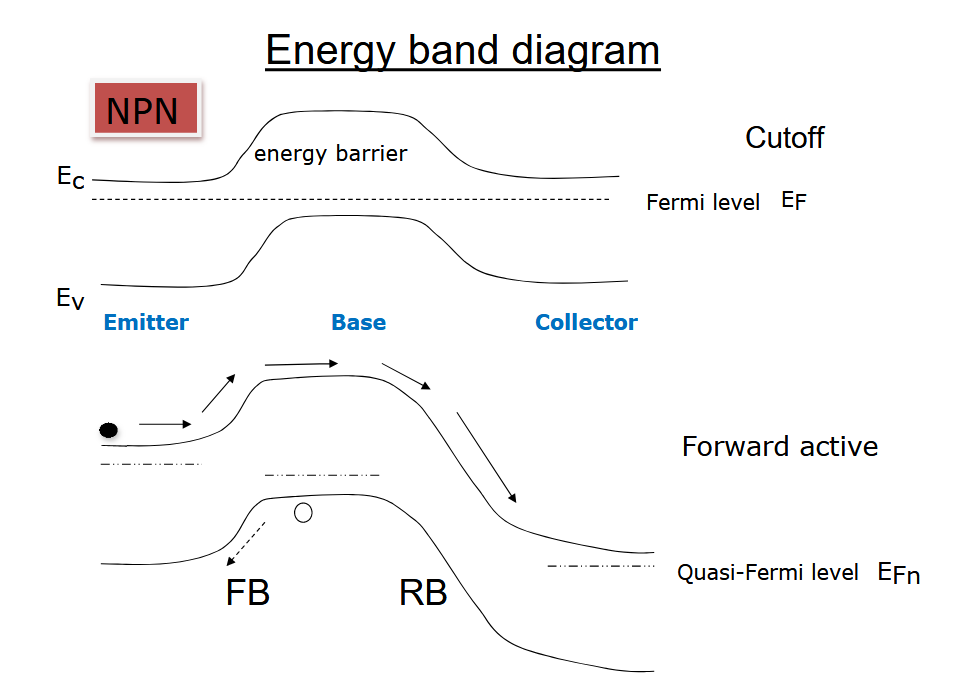
BJT 工作模式
BJT 有 4 个工作模式。

结基极-发射极反偏基极-发射极正偏
集电极-基极反偏截断（cut-off）前向偏置（forward active）
集电极-基极正偏反向偏置（reverse mode）饱和
从能带能更好地分析不同工作模式的区别。

工作模式感性认识

从能带进行分析

BJT 的正偏，实际上就是 EB 结势垒降低，BC 结势垒增加的结果。

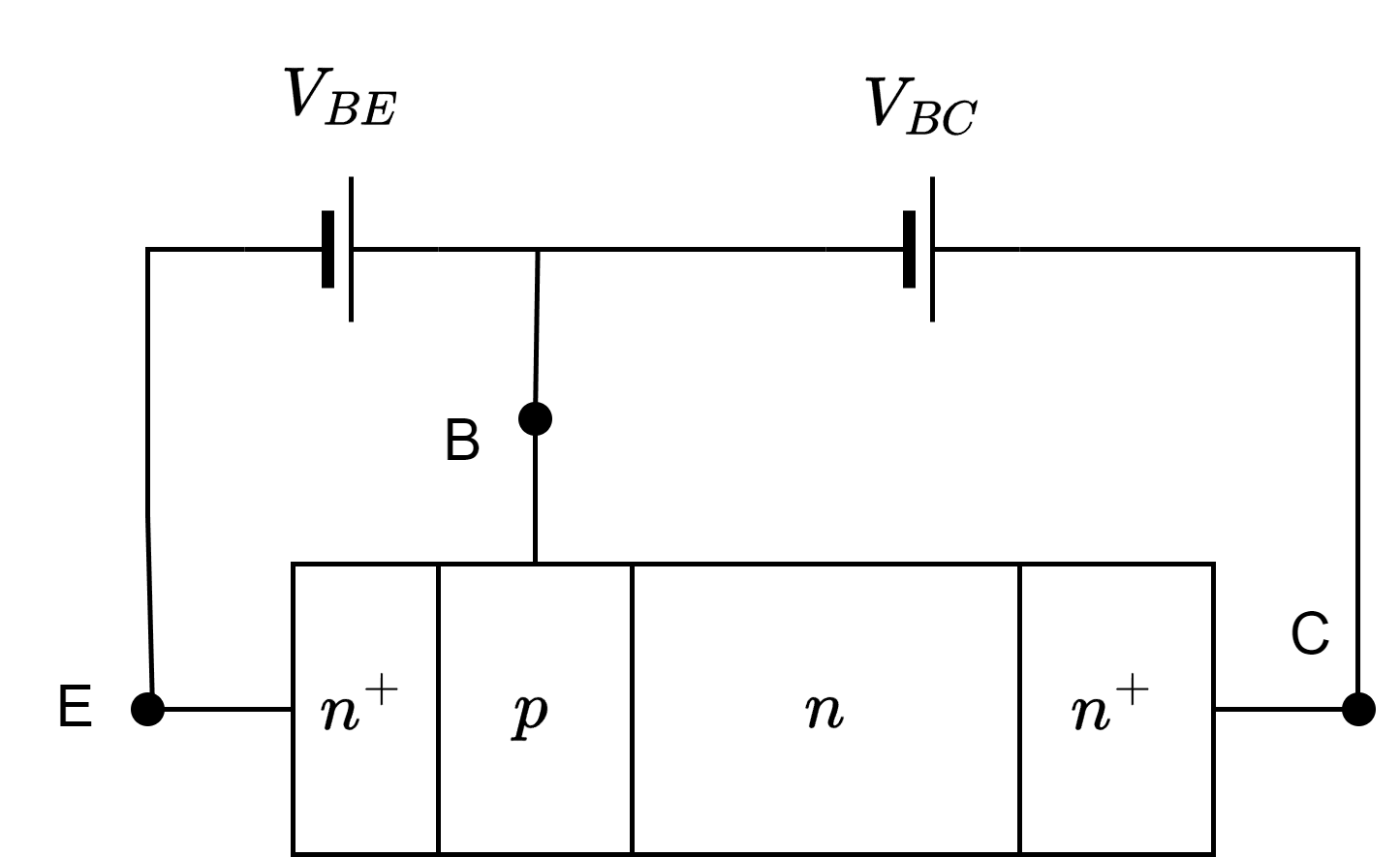
从 pn 结进行分析

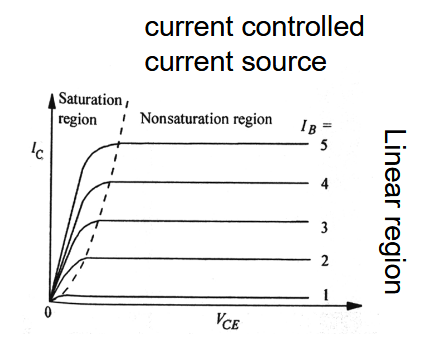
我们假设始终恒定，且使得 EB 结正偏。当，有 EB 结、BC 结同时正偏，BJT 工作在饱和模式。当，有 EB 结正偏，BC 结反偏，BJT 会工作在前向偏置模式，注入的电子全部汇入集电极。

由此可以看出，当恒定，一开始集电极电流随着的增加而增加。当大到使得 BJT 工作在正向偏置模式，此时集电极电流与无关。就像一个由基极电流控制的电流源。集电极电流特性的均匀间隔意味着理想双极晶体管的增益是恒定的并且与集电极电流无关。

实际双极晶体管的实验 I-V 特性并不理想。
指向原始笔记的链接

结	基极-发射极反偏	基极-发射极正偏
集电极-基极反偏	截断（cut-off）	前向偏置（forward active）
集电极-基极正偏	反向偏置（reverse mode）	饱和
从能带能更好地分析不同工作模式的区别。

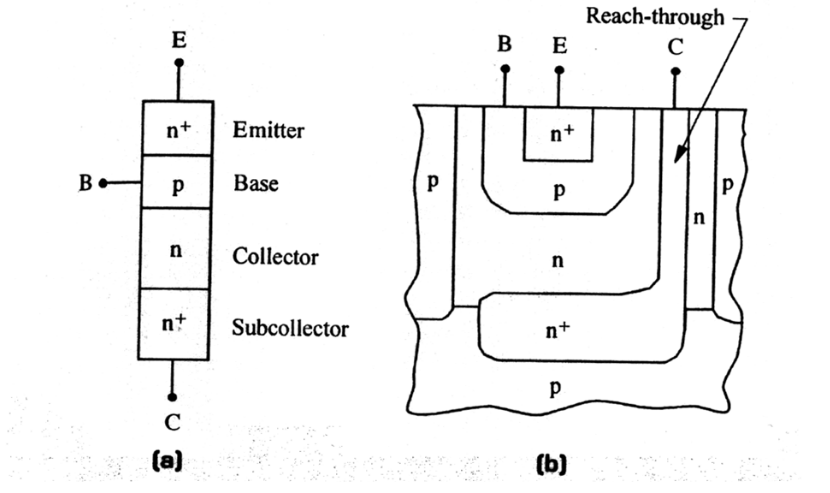
1.1.4. BJT 基本工作原理

BJT 基本工作原理
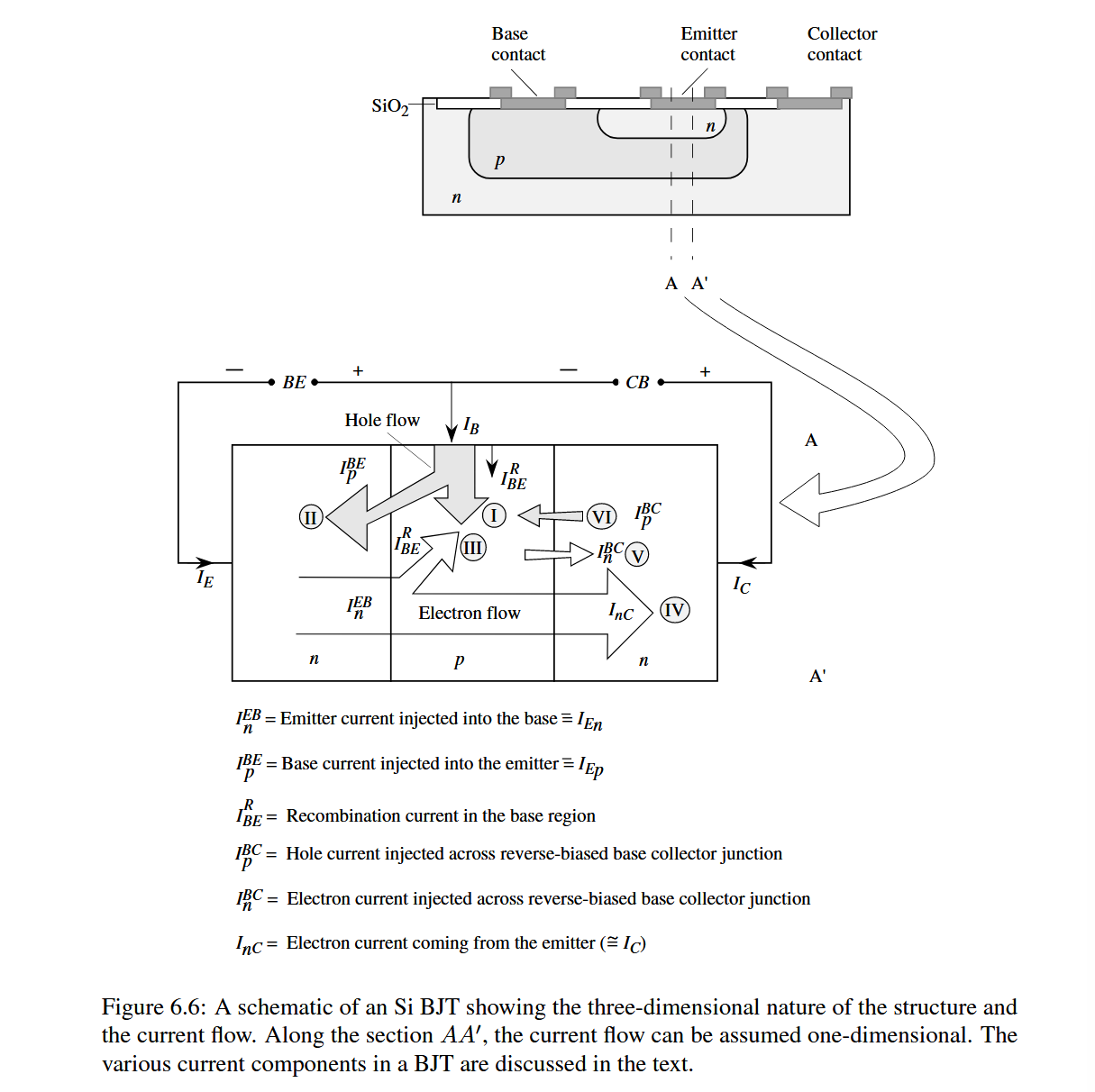
首先是需要认识到 BJT 是两个 PN 结反向串联，并且因为基极很薄所以靠得非常近。

当施加正向偏置电流的时候，n 型发射极中的电子通过扩散或漂移通过 BE 结的势垒进入基极成为少子。

随后少子穿过薄基区，并被 BC 结的高电场扫入集电极并提供电流。

同时，输入的基极电流也会分为两个部分，一部分空穴会从基极注入到发射极，另一部分会与基极中多余的电子复合。即上图中的 I 和 II 两部分。
指向原始笔记的链接

1.1.5. BJT 特性

BJT 特性
高跨导

能通过电压直接控制在集电极的载流子密度，跨导随着集电极电流线性变化。

高截断频率

垂直载流子传输允许制造尺寸控制极佳的结，无需光刻。可直接制造电子传输时间短、高的结构

高电流负载

整个发射极区域都会产生电流。可以用于实现功率器件。
指向原始笔记的链接

1.1.6. BJT 应用

BJT 应用
模拟

放大器（负反馈）

振荡器（正反馈）

RF 微波

用于无线通信的精密模拟电路（混频器、低噪声放大器、功率放大器…）

逻辑电路

高速逻辑电路

用在BiCMOS 中实现高速和高扇出

开关

信号控制

用于可再生能源和电动汽车的电力电子器件

指向原始笔记的链接

1.1.7. BJT 局限

BJT 局限

有限的直流输入基极电流；和 mosfet 相比较低的输入阻抗；

[! question] 为什么有限的直流输入和较低的输入阻抗会成为局限？

开启电压（）相对独立于器件几何形状和工艺参数。不能用作电路设计的变量。

器件在饱和状态下会储存大量电荷，导致开关缓慢。在这种情况下，器件实际上并不适合高速逻辑。

双极晶体管比 MOSFET 更难扩展。这意味着集成度较低，很难做到小型化。

由于硅带隙的原因，硅 BJT 无法在高温下工作。如需在高温下工作（如电力电子设备），应使用 SiC 和 GaN 等宽带隙半导体。

指向原始笔记的链接

1.2. 半导体器件物理基础

1.2.1. 载流子浓度

这里还有晶格和单晶材料的能带理论的内容，略过。

1.2.1.1. 热平衡载流子浓度

2021 #EE6604期末/2022 #EE6604期末/2023

通过导带顶、价带底、费米能级以及导带有效状态密度和价带有效状态密度，能分别计算出导带和价带中的载流子热平衡浓度

导带电子热平衡浓度公式

为导带有效状态密度；为导带底能量；为费米能级；为波尔兹曼常数；为温度
指向原始笔记的链接

价带空穴热平衡浓度公式

是价带有效状态密度，是价带顶能量，是费米能级，是玻尔兹曼常数，是温度。
指向原始笔记的链接

在载流子状态密度函数的计算中，导带和价带的有效状态密度是状态密度函数和费米-狄拉克分布函数相乘后在对应能带内的积分后得到的数学过程定义参数，无物理推导过程。后对状态密度函数和费米-狄拉克分布函数进行说明。

1.2.1.2. 状态密度函数

2022

状态密度函数
状态密度函数表示为单位体积单位能量中的量子态数量（能态总数），是系统中状态的一个固有属性。

一般模型

首先讨论一个被束缚在三维无限深势阱中的电子，而这个势阱就代表晶体的有状态密度函数。

有效状态密度函数公式

为电子的有效质量；为普朗克常数；为导带底的能量。
指向原始笔记的链接

可以看出，量子态密度是能量的函数，随着自由粒子能量的减弱，有效量子态的数量也逐渐减少。而且这个密度函数实际是双倍密度，也就是说，密度是在单位能量和单位体积中求得的。推导看这里

半导体模型

将一般模型拓展到整个半导体，确定导带和价带中的量子态密度。

导带底的电子状态密度

有效状态密度函数公式

为电子的有效质量；为普朗克常数；为导带底的能量。
指向原始笔记的链接

价带顶的空穴状态密度

价带空穴状态密度函数计算式

为空穴的有效质量；为普朗克常数；为价带顶的能量。
指向原始笔记的链接

推导看这里！
指向原始笔记的链接

1.2.1.3. 费米-狄拉克分布函数

2022

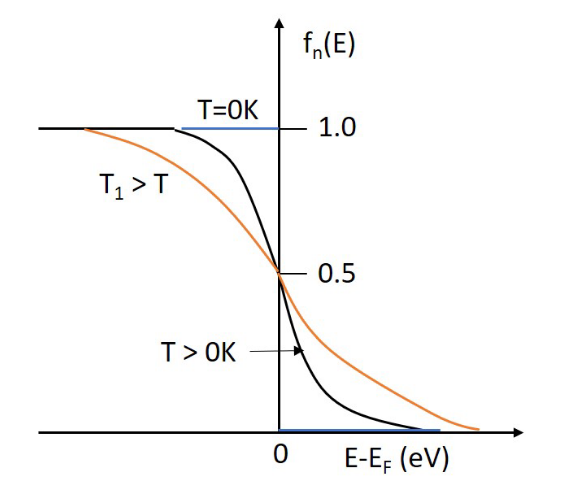
费米-狄拉克分布函数
费米-狄拉克分布函数代表了能量为的量子态被电子占据的可能性，另一种含义是被电子填充的量子态占据总量子态的比率。一个量子态如果没被电子占据即为空，或者说被空穴占据，由此可以导出量子态被电子和空穴占据的总概率为 1。

费米-狄拉克分布函数公式

能量为处，被填充的能量状态密度；为能量处的总的能量状态密度；为费米能级；为波尔兹曼常数；为开尔文温度。
指向原始笔记的链接

快速计算技巧：，能量每增加 60meV，概率增加一个数量级。当时，。

费米-狄拉克分布函数描述了在以费米能级为标准（50%，），在其他能量态出现电子的概率。左边靠近价带，右边靠近导带。

特点

粒子不可分辨，每个量子态只允许一个粒子。
指向原始笔记的链接

通过相乘并积分就能算出导带中电子和价带中的空穴。

[! note] 热平衡电子浓度

1.2.1.4. 本征载流子浓度

2021 #EE6604期末/2022

本征载流子浓度
在本征半导体中，由电中性原理可知，导带中的电子浓度等于价带中的空穴浓度。因此通常用来指代本征载流子浓度，它指热平衡电子浓度或者空穴浓度。

计算公式

本征载流子浓度计算式

为导带有效状态密度；为价带有效状态密度；为禁带宽度；为波尔兹曼常数；为开尔文温度
指向原始笔记的链接

为禁带宽度，硅为，碳化硅为；时，。适用条件：1. 热平衡状态；2. 非简并（轻掺杂）对于一个给定的半导体材料，的值和温度强烈相关而和费米能级无关。

想看推导过程可以戳这里

质量作用定律

对于任何热平衡状态下的半导体，有

这个是热平衡状态半导体的一个基础公式，是在玻尔兹曼近似的基础上推导而来的。
指向原始笔记的链接

1.2.2. 费米能级和准费米能级

没有被掺杂的半导体我们称为本征半导体。当我们考虑一个掺杂的半导体的时候，它的费米能级会随着掺杂而改变，因为费米能级是对电子分布的描述，而掺杂改变了这种分布。掺杂施主原子会使得价带中电子浓度增加，由此使得费米能级上移；掺杂受主原子则相反。

那价带顶和导带底会不会收到影响呢？会，因为这个是由晶体结构和能带性质决定，掺杂在一定程度上会改变结构和性质。但是这里我们先假设这种变化是微小且可以忽略的。

1.2.2.1. 本征半导体的费米能级

我们先介绍本征半导体中的本征费米能级。

本征费米能级
本征半导体的费米能级称为本征费米能级。其位置处于禁带中央附近。

费米能级计算式

为导带底能量；为价带底能量；为波尔兹曼常数；为开尔文温度；为空穴有效质量；为电子有效质量。
指向原始笔记的链接

[! note] 在非本征半导体中，也会把本征费米能级画出来作为参考。

指向原始笔记的链接

可以看出，本征半导体的本征费米能级几乎位于禁带中央，但是会因为电子和空穴的有效质量而偏移。

1.2.2.2. 非本征半导体的费米能级

非本征半导体的费米能级
非本征半导体意味着半导体被掺杂，对于 N 型半导体而言，

N 型半导体费米能级计算式

为本征费米能级；为施主原子掺杂浓度；为本征载流子浓度。
指向原始笔记的链接

对于 P 型半导体而言，，

P 型半导体费米能级计算式

为本征费米能级；为受主原子浓度；为本征载流子浓度
指向原始笔记的链接
指向原始笔记的链接

可以看到，费米能级能够衡量半导体的掺杂情况。并且在半导体处于热平衡的时候，费米能级是恒定的。

1.2.2.3. 波尔兹曼关系

2021

波尔兹曼关系就是用费米势去表示热平衡载流子浓度。费米势定义为，

费米势定义式

为费米能级；为电子电荷。
指向原始笔记的链接

[! note] 这里可以辅助理解外在电压是如何影响费米能级变化的。你施加正电压导致费米势增加，从而导致费米能级的降低。

用上面的式子代换到计算 N 型半导体和 P 型半导体的费米能级的公式中去（这里用掺杂浓度近似了多子浓度）

波尔兹曼关系
指向原始笔记的链接

1.2.2.4. 准费米能级

准费米能级
当半导体不处于平衡状态时（如电、光或热激发），前面的方程严格来说并不适用。此时，电子和空穴的分布不能用单一的费米分布描述，因此引入两个准费米能级：

电子准费米能级 ( )

空穴准费米能级 (）并写出类似的玻尔兹曼关系式：

非热平衡电子浓度
指向原始笔记的链接

非热平衡空穴浓度
指向原始笔记的链接
指向原始笔记的链接

准费米势能
同样可以用准费米势能来描述非平衡状态的载流子浓度

当半导体处于非平衡状态时，电子和空穴的准费米级分离。准费米级的分离是偏离平衡的标志。

运行设备中的载流子浓度可能会因电压或位置的不同而有许多数量级（十的幂次方）的变化。用准费米级来描述这些浓度更为方便，因为它与对数有关。

准费米能级给出了器件中的电流密度。
指向原始笔记的链接

将准费米势能公式沿着 x 进行积分可以分别得到电子和空穴的总电流密度公式。

1.2.3. 半导体中的电流

半导体中的电流分为漂移电流和扩散电流。

1.2.3.1. 漂移电流

根据欧姆定律，我们能将载流子的漂移电流密度写为，

电子漂移电流密度公式

为电子电荷；为电子浓度；为电子迁移率
指向原始笔记的链接

空穴漂移电流密度公式

为电子电荷；为空穴浓度；为电子迁移率
指向原始笔记的链接

1.2.3.1.1. 迁移率

迁移率
迁移率描述给定材料在平均电场作用下平均漂移速度，有定义式：

迁移率定义式

为平均漂移速度；为电场强度。
指向原始笔记的链接

载流子迁移率计算

根据定义可以推导出，
电子迁移率公式

是一个电子的带电量；是电子的有效质量；是电子的平均自由时间。
指向原始笔记的链接

推导看这里

空穴迁移率公式

是一个空穴的带电量；是空穴的有效质量；是空穴的平均自由时间。
指向原始笔记的链接

与电子迁移率推导具有同样的推导过程

散射的影响

散射也会对迁移率造成影响。

我们设为仅受杂质电离散射时的迁移率；设为仅受晶格振动散射时的迁移率。

由此可得，在两种散射共同影响下的迁移率为
指向原始笔记的链接

1.2.3.2. 扩散电流

扩散电流是半导体独有的，根据菲克定律有，电子的扩散电流，

电子扩散电流密度公式

为电子扩散系数；为电子的浓度梯度。
指向原始笔记的链接

和空穴的扩散电流，

空穴扩散电流密度公式

为空穴扩散系数；为空穴的浓度梯度。
指向原始笔记的链接

推导可以看这里

这里需要注意的是对于空穴和电子，其扩散电流的符号不一样。

总的扩散电流有，

总扩散电流密度

为扩散系数；为电子(空穴)的浓度梯度。
指向原始笔记的链接

实际上，载流子的迁移率和扩散系数是遵循着爱因斯坦关系的。

1.2.3.3. 电流密度方程

将载流子的漂移电流和扩散电流相加，就能得到分别的电流密度。

电子电流密度计算式
指向原始笔记的链接

空穴电流密度计算式
指向原始笔记的链接

以及半导体的总的电流密度，

总电流密度
指向原始笔记的链接

1.2.4. 载流子复合

2022

当载流子浓度从平衡状态受到扰动时（如受到光照或从结点注入），载流子浓度会自然回归到平衡值。这是因为平衡态是能量最低、最稳定的状态。这种恢复平衡的过程涉及过剩载流子的复合。

这里讲一讲最重要的 SRH 复合机理，这个机理同时适用于体内复合和表面复合。

SRH 复合
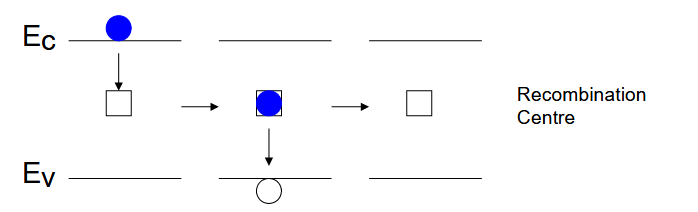
SRH 复合是和等间接带隙半导体的主要复合机制。

这种复合是非辐射的，载流子的过剩能量产生声子（晶格振动）。这涉及一个复合中心，一般是晶格缺陷，如位错（dislocations）、杂质原子（impurity atoms）。

当复合中心处于最中间时复合率最高。

动力学原理

电子从导带到复合中心，随后再到价带与空穴复合，并产生声子损失能量。

对于 P 型硅中的小注入电子而言，
P 型硅体内复合率计算式
$复合率$
为电子少子寿命；为热平衡电子浓度；为电子浓度
指向原始笔记的链接
指向原始笔记的链接

为什么不直接跨越能带间隙进行复合

1.2.5. 表面复合

2022 #EE6604期末/2023

半导体晶体的表面布满缺陷，例如来自晶面末端的悬空键和来自环境的杂质。这些导致表面态的分布和表面附近的能带弯曲。因此，非辐射复合在非钝化半导体表面上会以更高的速率发生。

1.2.5.1. 表面复合速率

p 型半导体表面的复合率和体内复合率类似但是不同，

P 型半导体表面复合率
$表面复合率$
为表面复合速度；表面面积；为电子浓度；为热平衡电子浓度
指向原始笔记的链接

[! note] 这里再说明一下「复合率」是个什么东西。复合率就是单位时间内发生的复合事件次数，而一次空穴和电子合并然后产生声子就是一次复合事件。由此我们可以通过复合率来计算电流密度，P 型半导体表面复合电子电流密度计算式和 N 型半导体表面复合空穴电流密度计算式。

2. 先进二极管理论——BJT 的紧凑模型

2.1. 基本假设

2.1.1. BJT 分析的基本假设

两个耗尽区中的复合和生成过程对电荷流的贡献可以忽略不计。
发射极、基极和集电极均匀掺杂，因此耗尽区之外没有内置电场。
发射极和集电极区域与这些区域中的少数载流子扩散长度相比较宽。

2.1.2. 基本假设的问题

BJT 的简单理论只能用于不切实际的简单器件结构。当它应用于真实设备时，它们往往会给出错误的预测，因为它们没有考虑到几个重要的效应。

例如其第二点，说耗尽区之外没有内置电场，但是实际的 BJT 的基极内存在电场。所以 CM 会假设基极是均匀掺杂的并且重掺杂。

因此需要使用 Moll-Ross 理论建立的紧凑模型。

2.2. 紧凑模型的假设

2021 #EE6604期末/2023

现做出以下假设：

忽略所有的寄生电阻以及相关的压降；
忽略基极中发生的复合；
集电极电流仅由从发射极注入基极的电子产生；
基极电流由从基极注入到发射极的空穴产生。

对于 BJT 紧凑模型的理解

2.3. 基极和发射极的电流密度

2.3.1. p 型基极中电子的电流密度方程

后面的公式都是在下面的 BJT 一维建模上进行的。

根据电子漂移电流密度公式、电子扩散电流密度公式、爱因斯坦关系式以及电场的定义，我们可以将在 P 型基极中的电子总电流密度公式重写为包含准费米能级的形式，

用准费米势表示 P 型基极中电子总电流密度

为电子电荷；为基极中电子浓度；为电子迁移率；为电子准费米势
指向原始笔记的链接

用准费米势表示 P 型基极中电子总电流密度推导过程

因为在基极中空穴准费米能级近乎恒定（因为 BJT 正偏时仅有空穴的复合会产生电流，但是基极的复合又是可以忽略的），于是有，所以可以将上式再重写为，

考虑重掺杂效应，有，

[! question] 为什么不考虑大注入？ CM 是这样假设的。

代入后得到，

BJT 紧凑模型 P 型基极电子电流计算式

为电子电荷；为电子的扩散系数；为有效本征载流子浓度；为 p 型基极中空穴浓度；为 p 型基极中电子浓度
指向原始笔记的链接

这样就能通过基极电子和空穴浓度来计算基极中电流密度。

2.3.2. n 型发射极中空穴的电流密度方程

同理，给出公式，

BJT 紧凑模型发射极空穴电流密度计算式

为电子电荷；为空穴的扩散系数；为有效本征载流子浓度；为 n 型发射极中空穴浓度；为 n 型发射极中电子浓度。
指向原始笔记的链接

为什么要用载流子浓度去计算基极和发射极电流密度

2.4. 集电极电流和基极电流

2.4.1. 集电极电流

2021 #EE6604期末/2023

由基极电子电流密度推导集电极电流过程

有集电极电流为，

BJT 紧凑模型集电极电流计算式
指向原始笔记的链接

定义为饱和集电极电流密度，

集电极饱和电流密度

为基区古梅尔数。
指向原始笔记的链接

基区古梅尔数定义为，

基极古梅尔数计算式
指向原始笔记的链接

[! note]

古梅尔数的定义考虑了基区重掺杂的影响。

集电极电流仅是基本参数的函数。

集电极电流不依赖于发射极的特性。

2.4.2. 基极电流

2023

由于没有电子复合，基极电流只是由基极到发射极的空穴注入电流构成。由于发射极的重掺杂，有，于是可以把前面的 BJT 紧凑模型 N 型发射极空穴密度计算式重写，

BJT 紧凑模型发射极空穴电流密度计算式

为电子电荷；为空穴的扩散系数；为有效本征载流子浓度；为 n 型发射极中空穴浓度；为 n 型发射极中电子浓度。
指向原始笔记的链接

从公式可以看出，基极电流仅仅和发射极参数相关，与基极的性质无关。

2.4.3. 浅发射极的基极电流

当发射极的宽度小于发射极少数载流子扩散长度时，发射极是浅掺杂或透明的。对于这种特殊情况，Jp (x) 与 x 无关。同样将从公式两边积分为，

这里需要注意的就是我们是从发射极欧姆接触（）积分到的位置。

在处，通过正偏电压下 pn 结 n 区内少子空穴浓度计算式计算空穴浓度，

在处，由于是欧姆接触，于是我们用表面复合速率去计算空穴浓度，

浅掺杂发射极 BJT 基极电流密度计算式
指向原始笔记的链接

这仅适用于浅发射极 BJT，但对任意掺杂分布都有效。

有基极电流为，

浅掺杂发射极 BJT 紧凑模型基极电流计算式

为基极饱和电流密度；
指向原始笔记的链接

基极饱和电流密度计算式为，

基极饱和电流密度计算式
指向原始笔记的链接

浅发射极的发射极古梅尔数为，

浅发射极的发射极古梅尔数
指向原始笔记的链接

2.4.4. 小总结

基极电流能写作，

浅掺杂发射极 BJT 紧凑模型基极电流计算式

为基极饱和电流密度；
指向原始笔记的链接

集电极电流能写作，

BJT 紧凑模型集电极电流计算式
指向原始笔记的链接

基极电流和集电极电流均与 VBE 呈指数关系。

有基极饱和电流密度，

基极饱和电流密度计算式
指向原始笔记的链接

和集电极饱和电流密度，

集电极饱和电流密度

为基区古梅尔数。
指向原始笔记的链接

再回顾基极古梅尔数

基极古梅尔数计算式
指向原始笔记的链接

和发射极古梅尔数，

发射极古梅尔数定义式
指向原始笔记的链接

取决于基极古梅尔数，

取决于发射极古梅尔数。

2.5. BJT 跨导

2022

BJT 的跨导定义为，

BJT 跨导定义式

为电子电荷；为 BJT 集电极电流；为波尔兹曼常数；为绝对温度
指向原始笔记的链接

BJT 跨导计算式
指向原始笔记的链接

2.6. 电流增益

2022

共基极电流增益为，

共基极电流增益

为集电极电流；为发射极电流
指向原始笔记的链接

共发射极电流增益为，

BJT 共发射极电流增益定义式

为集电极电流；为基极电流
指向原始笔记的链接

通过将基极电流和集电极电流代换，能够得到

再代入两个古梅尔数的定义式，对于浅发射极有，

这样，通过掺杂浓度和发射极宽度就能直接计算得到共发射极电流增益。

再根据共基极电流增益和共发射极电流增益的关系，可以计算出，

共基极电流增益

为集电极电流；为发射极电流
指向原始笔记的链接

一般情况下，接近 1 并且小于 1，由此会相当大，在目前的 VLSI 中，至少为 100。作为 BJT 进行分析的品质因子，对于模拟应用非常重要。

2.7. 理想特性

BJT 理想 I-V 特性

当时，晶体管处于饱和模式。当时，npn 晶体管处于正向偏置模式。集电极-基极反向偏置，收集所有注入的电子。

[! note] BJT 先是饱和区，然后是线性区。和 MOS 相反。

集电极电流随着的增加而增加，因为是两个电子注入电流的差值。

我们总是更关注线性区，因为在正向偏置区工作的 BJT 的集电极电流与无关。就像一个由基极电流控制的电流源。
指向原始笔记的链接

2.8. 古梅尔图

2021 #EE6604期末/2023

古梅尔图
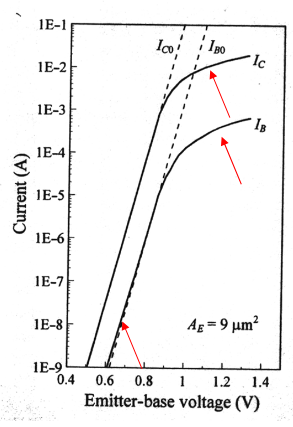
古梅尔图是双极型晶体管（Bipolar Junction Transistor, BJT）的一种常用特性曲线图，用于描述基极-发射极电压 VBE 与集电极电流 IC 和基极电流 IB 之间的关系。

versus

指向原始笔记的链接

只在以及均为线性的时候，才是常量。

可以看到在高 VBE 下，测得的 Ic 通常小于理想晶体管 (IC0)。在高 VBE 时，测得的 IB 通常也小于 IB0，但在低 VBE 时则高于 IB0。

[! summary] 这里总结一下实际电流和理想电流出现偏差的原因。原因的具体内容在 3. 非理想 BTJ 行为有叙述。

小注入时，高于理想值

基极中的复合-产生电流

基极中的隧穿电流

大注入时，低于理想值

发射极和基极的寄生电阻、和

大注入时，低于理想值

发射极和基极的寄生电阻

基极电导调制效应

由此得到的共发射极增益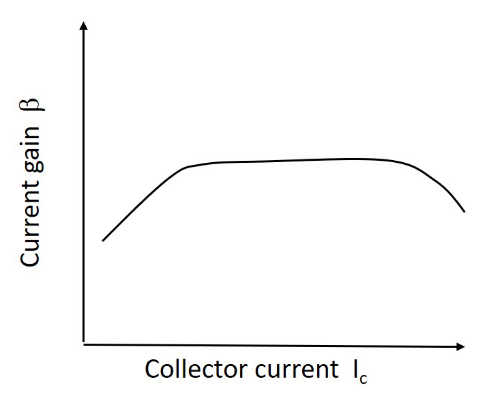如下，电流增益与 IC 的关系不是恒定的。仅在 IC 和 IB 接近理想的区域内保持恒定。对于小 IC，由于 IB 增加，减小。对于大 IC，减小，因为 IC 比 IB 减小得更快。

3. 非理想 BTJ 行为

3.1. 发射极和基极的寄生电阻

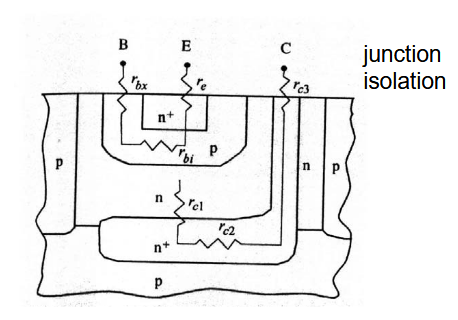
从上面这张图可以看出来寄生电阻在 BJT 中的分布，但是我们主要关注、和这三个寄生电阻。

为发射极串联电阻（接触电阻）。发射极重掺杂且薄，使得接触电阻主导；
本征基极电阻（轻掺杂区域）
非本征基极电阻（连接基极接触和本征区域的高掺杂区域）集电极寄生电阻都可以忽略不计。

由于发射极和基极的寄生电阻，BE结会有一个压降存在。

实际上的 BE 结电压为，

所以高的时候，IC 和 IB 会下降

3.2. 基极电导率调制效应

2023

这是导致 IC 在高下降低的另一个效应。

在高水平的电子注入下，基极中的空穴浓度必须通过热生成而增加，以保持电荷中性（指电流连续性）。
此外，注入的电子会增加 BC结基极侧的负空间电荷。这减少了耗尽宽度并增加了准中性基极宽度。

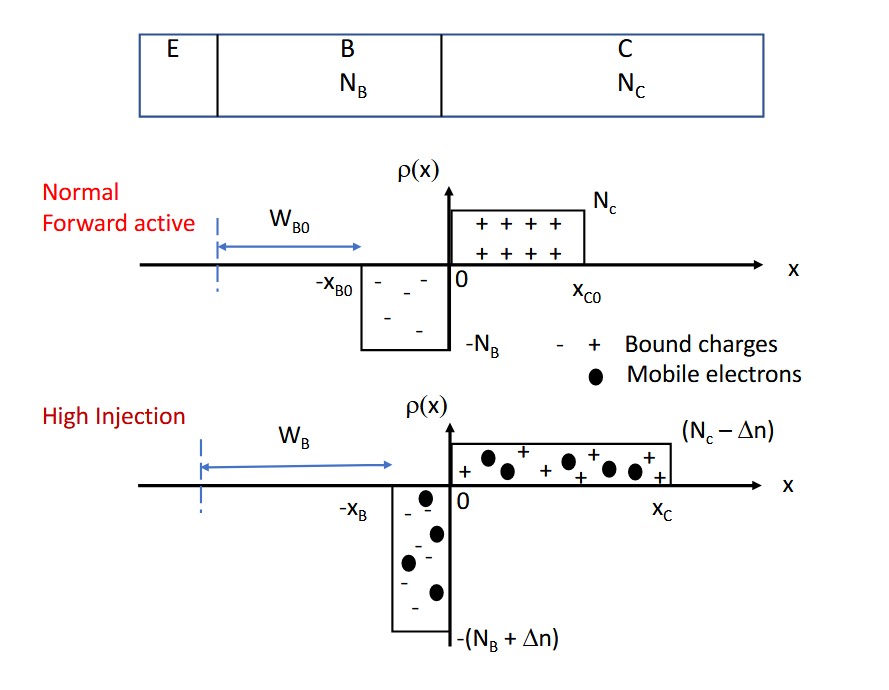从上图可以看出，当大注入的时候，BC 结中基区的耗尽区的电子浓度更高，由此耗尽区宽度减小；而集电极的耗尽区空穴浓度降低，由此需要更宽的耗尽区。

基极古梅尔数计算式
指向原始笔记的链接

(1) 和 (2) 都增加了基极古梅尔数并降低了。

3.3. 非理想基极电流

基极电流由三个分量组成：

从基极到发射极的空穴注入电流
产生-复合电流
隧道电流

在理想晶体管理论中只考虑了第一个分量。而在低偏置电压下，电流 (2) 和 (3) 会导致偏差。

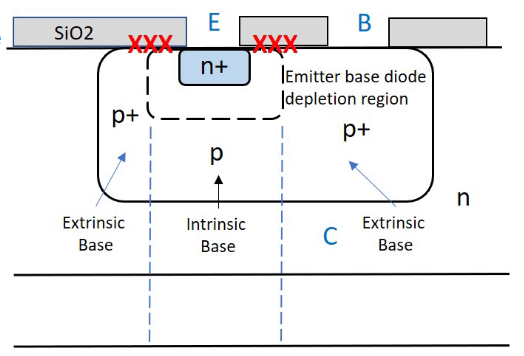
3.3.1. 基极中的产生-复合电流

该电流分量是由基底表面的界面态 (x x x) 引起的。它们位于界面处。由于这些状态位于 Si 带隙内，因此它们可能导致 SRH 复合。注入的载流子会复合，而不是穿过基极到达集电极。由于半导体工艺的改进，这不再是问题。

3.3.2. 基极中的隧道电流

2023

当发射极和外基极都存在重掺杂时，发射极-基极结处的带间量子隧穿是可能的。窄耗尽宽度与德布罗意电子波长相当。对于 VLSI 双极晶体管来说很重要的是，带间隧道电流与温度无关。

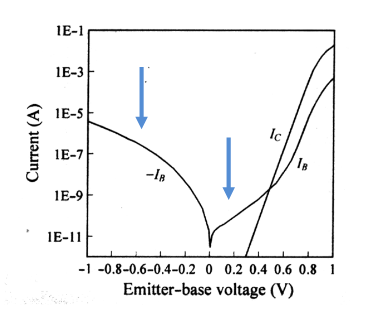可以看到低偏置电压的时候，出现了非常高的偏移，并且在负偏置电压的时候，BE 结没有像正常的 pn 结一样仅仅有反向偏置电流。这就是带间量子隧穿的展现。

3.3.2.1. pn结中的带间量子隧道

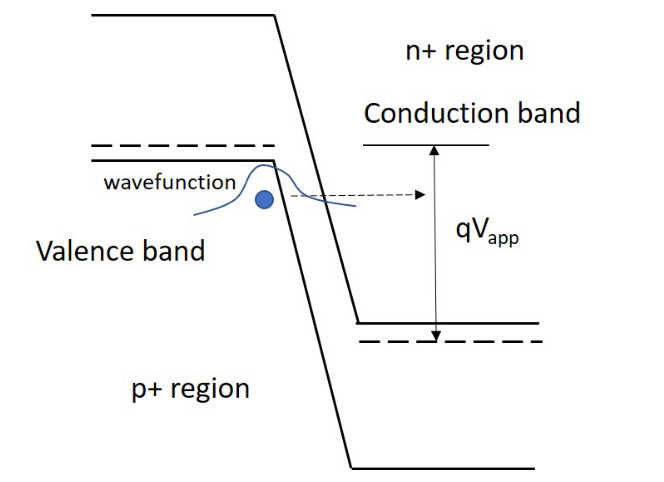在反偏条件下，并且两边都是重掺杂的情况，价带电子就直接通过量子隧穿到导带中去。

3.3.3. 厄利效应

2022 #EE6604期末/2023

厄利效应
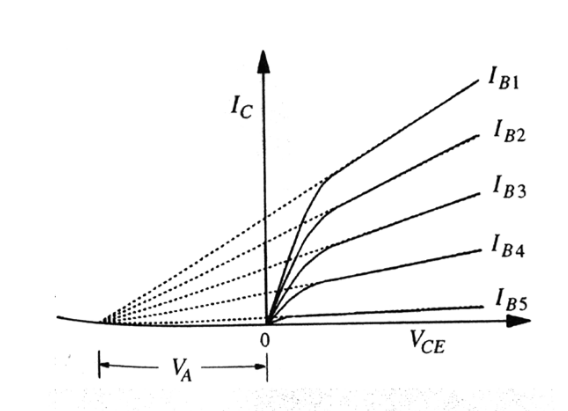
厄利效应是指在具有轻掺杂薄基极 BJT 中，集电极电流通常随着集电极发射极电压的增加而增加。

这种效应是由基极集电极耗尽宽度的增加引起的。结果，准中性基底宽度 WB 减小。

厄利电压

厄利电压是描述双极型晶体管（BJT）中集电极电流随集电极-发射极电压 () 变化的敏感度的参数。它表征了 BJT 的输出特性曲线在理想情况下是否接近平坦，并间接反映了器件中电流增益的稳定性。

厄利电压非常大，至少 100V。集电极电流在线性区域内随 VCE 线性增加。当外推的集电极电流等于 0 时的集电极电压称为厄利电压。
厄利电压计算式
指向原始笔记的链接
VA 随着基极掺杂密度的增加而增加。如果基极掺杂非常轻（小），准中性基极宽度会减小到零并发生穿通。穿通也就是基极两边的耗尽区直接相接。
指向原始笔记的链接

3.3.4. 结击穿

在看这里之前，需要先了解4.1. 基本直流 Ebers-Moll 模型

3.3.4.1. 基极-集电极碰撞电离

如果双极晶体管具有较大的，但是由于结碰撞电离，集电极电流仍会随着基极-集电极电压的增加而增加。这导致载流子倍增。

从发射极注入的电子进入反向偏置的集电极-基极耗尽区并获得能量。

高场通过破坏 Si-Si 键导致碰撞电离，二次电子增加集电极电流，次级空穴流向基极并降低基极电流。

3.3.4.2. 击穿电压

对于 BJT，通常是让其中一个端子浮空（开路），然后反向偏置另外两个端子。

集电极基极击穿电压（发射极 OC）
集电极发射极击穿电压（基极 OC）

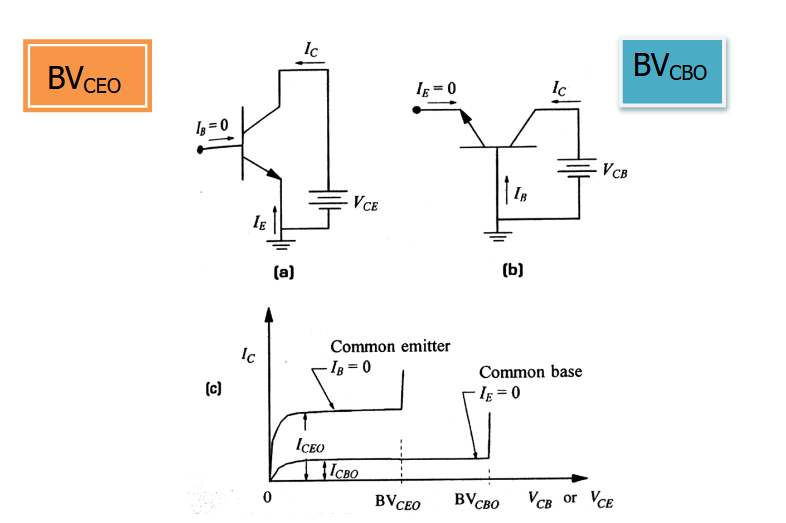和通常需要足够大，而没有实际意义。BV 可以通过以下的电路进行测量，可以从上图看出且。当电压小于击穿电压的时候，电流具有和 pn 结反向偏置电流一样的行为，当电压大于击穿电压时，电流陡增。

3.3.4.3. 载流子的雪崩倍增

当发生雪崩击倍增的时候，离开集电极基极耗尽区的电子电流比进入它的电流大 M 倍。于是我们定义

为发射极注入效率，定义为，

发射极注入效率定义式

为基极处的电子电流密度；为基极处的空穴电流密度
指向原始笔记的链接

为基极传输因子，定义为，

BJT-基极传输因子定义式

对于没有击穿的情况（），相当于有，

3.3.4.4. BJT 饱和电流的关系

根据 Ebers-Moll 模型重写电流公式为，

用 Ebers-Moll 模型推导击穿电流关系

可以得到发射极开路时，集电极基极二极管的反向饱和电流。

对于电路，，，因此有，

这里，基极浮空的反向偏置电流。

这里看出来，是比更大的（）。当击穿发生的时候，，趋于无穷。

也就是电路雪崩击穿的条件。

3.3.4.5. 和之间的关系

对于 BV 之间的关系，我们需要使用经验结论。 Miller 发现倍增因子 M 通常可以用反向偏置 pn 结的击穿电压表示为：

用反偏 pn 结击穿电压表示的倍增因子计算式

是反偏电压；是 3-6 之间的经验数。
指向原始笔记的链接

我们将这个公式代入

电路。对于

电路中正偏的晶体管的集电极-基极结而言，有倍增因子，

在击穿时 M 无穷大（当电压到达击穿电压的时候）。

对于电路，击穿时，我们可以用去近似。

Question

没懂他这里怎么近似的，为什么可以近似

然后可以得到，

这里就发生了替换了。

当击穿发生时，倍增系数 M 不会无限大，而是接近于 1（但稍大于 1），这个条件比无穷大更容易实现和满足。

因为有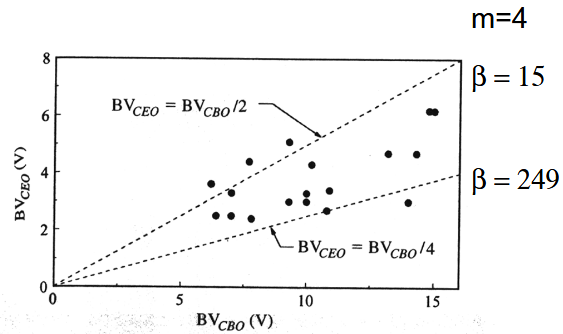，所以。从上图可以看出，当时，和总是在斜率 2.5 和 5 这个区间之间

3.3.4.5.1. 关于为什么会比更小的物理解释

对于每次基极-集电极结发生的雪崩击穿而言，总有电子空穴对产生。生成的二次电子会随着原本的电子一同进入集电极。

因为基极很薄，所以二次空穴能流向发射极（形成小注入）。并且由于此时发射极-基极二极管处于正偏，的电子从发射极注入基极，导致电流在较低电压下快速建立，并继续引发雪崩击穿。

[! question] 所以只说了配置下的情况，配置下为什么不会有类似的机制？

4. BJT 器件紧凑模型

前面的 BJT 紧凑模型相当于一个基础，BJT 器件紧凑模型使得电路模拟器能够来模拟包含 BJT 的电路。

器件的电气特性在模型中通过等效电路参数来表示。有两种广泛使用的直流模型：

Eber-Moll 模型
Gummel-Poon 模型（能够模拟非理想效应）

4.1. BJT 直流模型

4.1.1. 基本直流 Ebers-Moll 模型

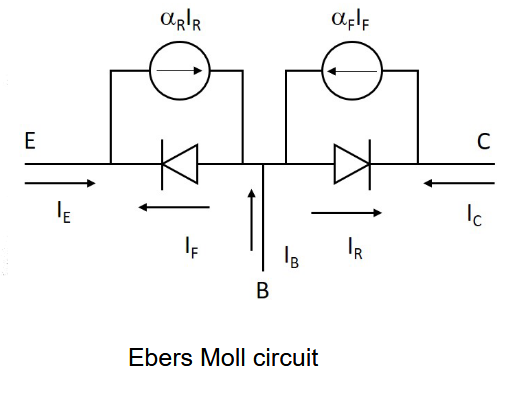Eber-Moll 模型由四个器件构成，两个受控电流源和两个二极管。

将这个和 BJT 工作模式对应起来看就可以理解了。然后下面来解释一下这两个受控电流源。

对从发射极注入到集电极的少子进行了建模。则是共基极正向偏置电流增益。

对从集电极注入到发射极的少子进行了建模。则是共基极反向偏置电流增益。

我们先来看和根据电路模型可以写出，

对于理想二极管，有理想 pn 结电流计算式，由此导出和并代入到上面两个公式中，得到下面两个公式，

这两个公式有助于我们理解碰撞电离。

然后再将上面两个公式重写为二端口网络的形式，

这里有网络参数，

这里假设网路是互易的，于是根据二端口网络的互易定理有，

所以，对于给定的双极晶体管，Ebers-Moll 模型参数：( $、、、$ ) 或 ( $、、、$ ) 可以从晶体管掺杂剂尺寸、掺杂分布和材料参数推导出来。

4.1.2. Ebers-Moll 模型的共发射极形式

为了在高频下分析电路而使用这个模型。

这是用于电路分析的 Ebers-Moll 模型的一种更有用的形式。可以从共基极模型推导出来。输入是 B 端，输出是 C 端，E 端在中间。

这种形式下，不仅能获得电压增益，也能获得电流增益，由此也获得了功率增益。

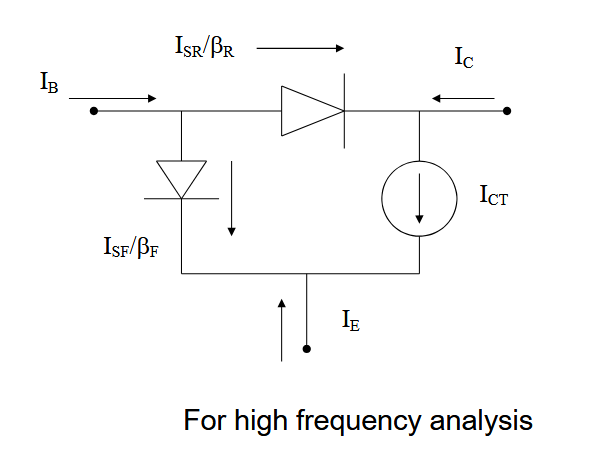
4.1.3. 从基本 CB EM 模型到 CE 模型

需要推导

4.2. 双极晶体管的小信号交流模型

2023

当存在交流信号时，必须将电容器添加到直流模型中。对于每个结而言，我们需要增加以下的电容器，

耗尽层电容，
扩散电容，

在共发射极 Embers-Moll 模型的基础上增加需要考虑的电容。

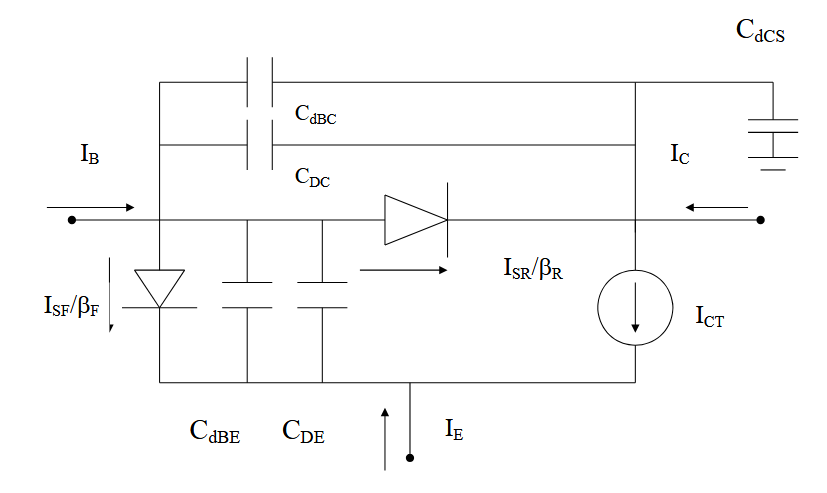
当小信号 (ss) 叠加在直流偏置电压上时使用。

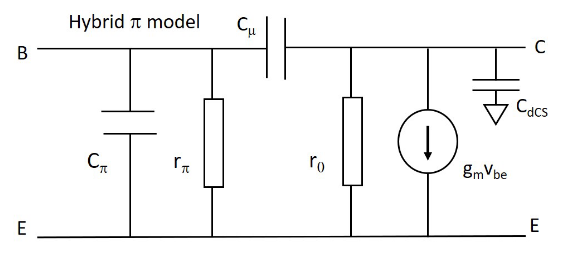
后面会逐步推出如何从共发射极的 Ember-Moll 模型到这个模型

小信号基极电流小信号集电极电流小信号基极-发射极电压小信号集电极-发射极电压

4.2.1. 模型参数

跨导是直流偏置点处相对于的比值。参考公式

参考 BJT 紧凑模型集电极电流计算式

BJT 跨导计算式
指向原始笔记的链接

由于热电压是固定值，于是通过改变

就能改变

。

输入阻抗 是和的比值。参考公式浅掺杂发射极 BJT 紧凑模型基极电流计算式

输出阻抗 是和的比值。

电容由以下指定，

是基极集电极结耗尽区的小信号电容。是基极发射极结耗尽区的小信号电容。称为发射极扩散电容。

如果寄生电阻很大，则应在这个理想的小信号模型中添加额外的电阻。

4.2.2. 扩散电容

2021

扩散电容是基极-发射极正向偏置所引起的所有少数载流子导致的寄生电容。

、在发射极、基极的少数载流子。、基极-发射极、基极-集电极空间电荷区的少数载流子。

每当晶体管内多余电荷重新排列时，都会引起端电压的变化。为了电路建模的目的，我们经常写，

发射极延迟时间; 基极渡越时间; 基极发射极耗尽区渡越时间；基极集电极耗尽区渡越时间。

我们定义一个前向渡越时间为，

在低时，与无关。

在高下，由于基极电导率调制效应，不是恒定的。

4.2.3. 少数载流子电荷分布

npn BJT 用于放大时的少子分布。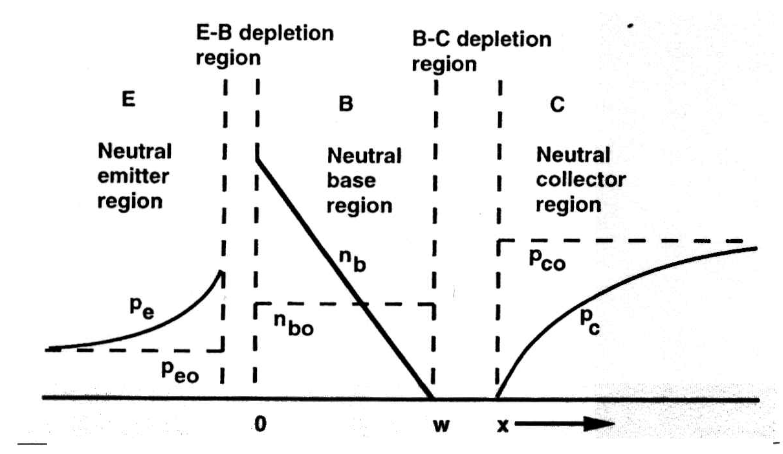当输入电流改变的时候，少子分布也会改变。

4.3. BJT 的瞬态和交流响应

BJT 的瞬态和交流特性由器件中存储的少数电荷决定。当端电压改变时，存储的少数电荷必须做出响应而改变，并且为此需要时间。

BJT 的高频性能的主要品质因数 (FOM)：

截止频率，
最大振荡频率，

4.3.1. 截止频率

2021 #EE6604期末/2022 #EE6604期末/2023

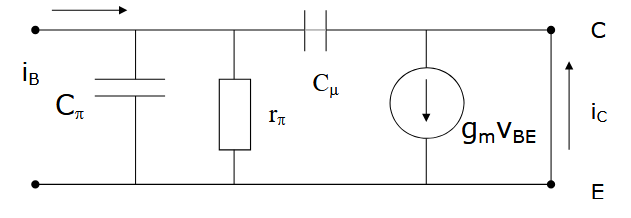定义为发射极和集电极短路时（），共发射极小信号电流增益降至单位 1 时的渡越频率。因此，它也称为单位电流增益频率。描述晶体管用作放大器时的最大有用频率，超出截止频率后 BJT 不在有放大作用。

有集电极电流和基极电流，

与频率相关的共发射极电流增益：

可以证明，，因此在高频下，

如果想要增大截止频率，就需要减小结电容，由其是扩散电容。所以扩散电容会减小 BJT 的截止频率。

再代入结电容，

前向渡越时间计算公式
指向原始笔记的链接

这也是用于计算前向渡越时间的常用公式。

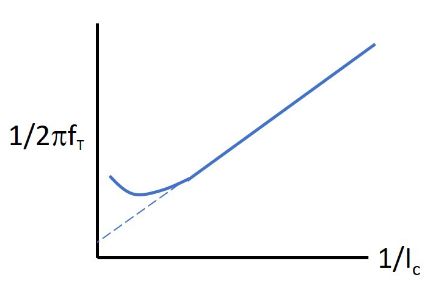根据上面这个公式可以画出以为横坐标，为纵坐标的图。虚线延长线即交于。

Question

为什么小的时候，会有偏差？是基极电导率调制效应引起的（可以结合古梅尔图来看）。

4.3.2. 最大振荡频率

2021

这是晶体管的最大资用功率增益降至 1 时的频率。

通常大于，因为它考虑了电压增益。

这里说明了最大振荡频率为什么会比截止频率高。

在高频的时候，有，

[! note] 这里可以看出，当扩散电容越大，越大，电压增益越小。

4.3.3. 的高频等效电路

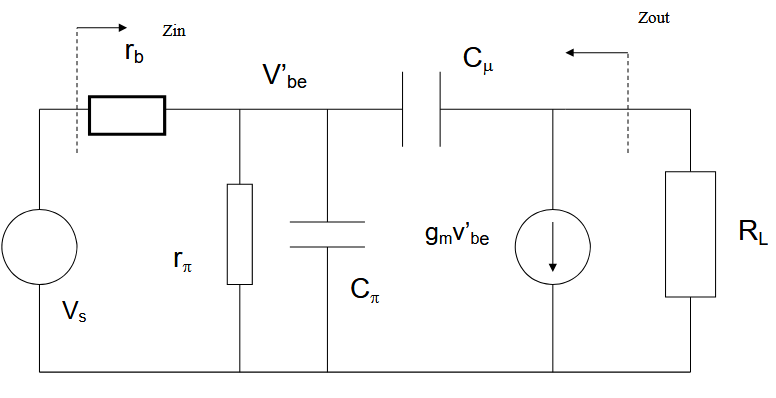
这个电路引入了和。

4.4. 最大资用功率增益

通过使用 VNA 才能测得最大资用增益（MAG）。

4.5. BJT 的频率响应

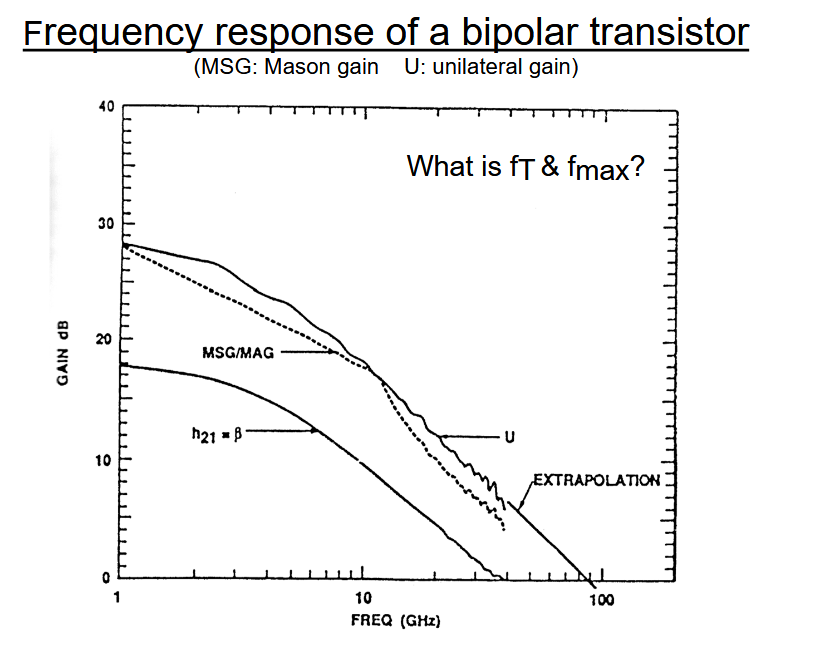
当时，有；当时，有。

5. 先进双极管

这一部分，了解不同先进晶体管为了解决什么问题出现即可。

5.1. 单、双多晶硅发射极晶体管

5.2. 扩散发射极的限制

发射极结深度通常必须深于 300nm（Si 中的少数载流子扩散长度）。
对于扩散发射极，基极宽度不能做得小于 100nm。

5.3. 多晶硅发射极晶体管

5.3.1. 关键特征

发射极深度：（典型值）
基极宽度:

5.3.2. 特性

更高的电流增益
更高的截止频率（因为渡越时间减少）
更少的寄生电容和电阻
更小的面积（通过使用自校准发射极）

5.3.3. 电流增益

需要注意的是，这里所说的多晶硅发射极晶体管的发射极仍然是单晶硅，但是和发射极接触的不再是金属，而是多晶硅。

通过使用多晶硅接触，来自基极的多余少数载流子（空穴）不需要像欧姆接触情况那样完全复合。

更小的表面复合速度使得基极电流更小。

5.3.4. npn 双极晶体管（多晶硅发射极）的垂直掺杂分布

多晶硅层具有两个功能：

形成浅发射极结的扩散源，
浅发射极区的接触电极。

“单多晶”多晶硅发射极晶体管：仅发射极与掺杂多晶硅接触。 “双多晶”多晶硅发射极晶体管：发射极和基极均由掺杂多晶硅接触。

5.3.5. 双多晶硅自校准发射极 CVD 流程

2022

原位沉积掺杂 p+ 多晶硅（多晶硅 1）和二氧化硅（原位：沉积和掺杂）
使用选择性蚀刻（未蚀刻基板）进行反应离子蚀刻氧化物和多晶硅 1
在蚀刻上方生长热氧化物结构; 100-400nm 多晶硅侧壁
硼从 p+ 多晶硅扩散形成外基极（和 3 同时发生）
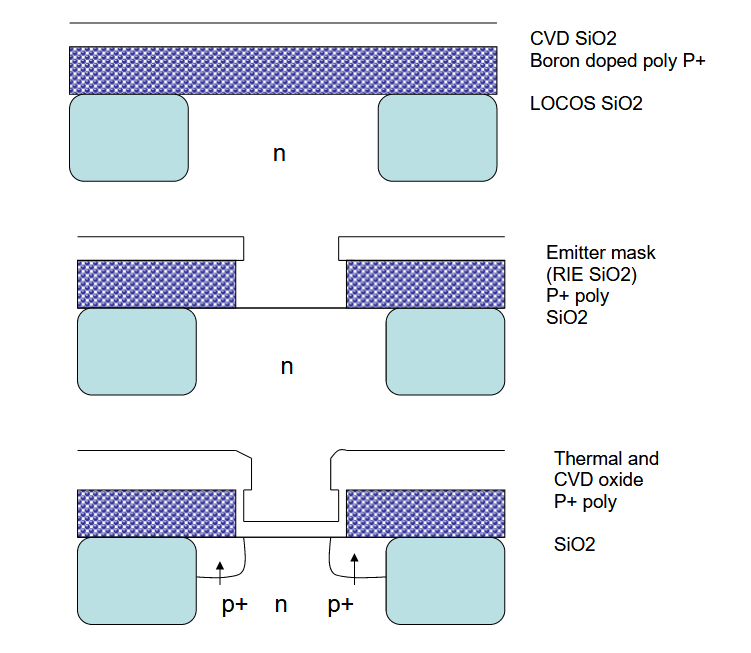
用硼植入内基（自对准非本征和本征基极）
清洁发射极接触窗 (HF/H2O)
沉积多晶硅 (poly2) 并注入砷
通过砷掺杂剂的外扩散形成浅发射极（）。

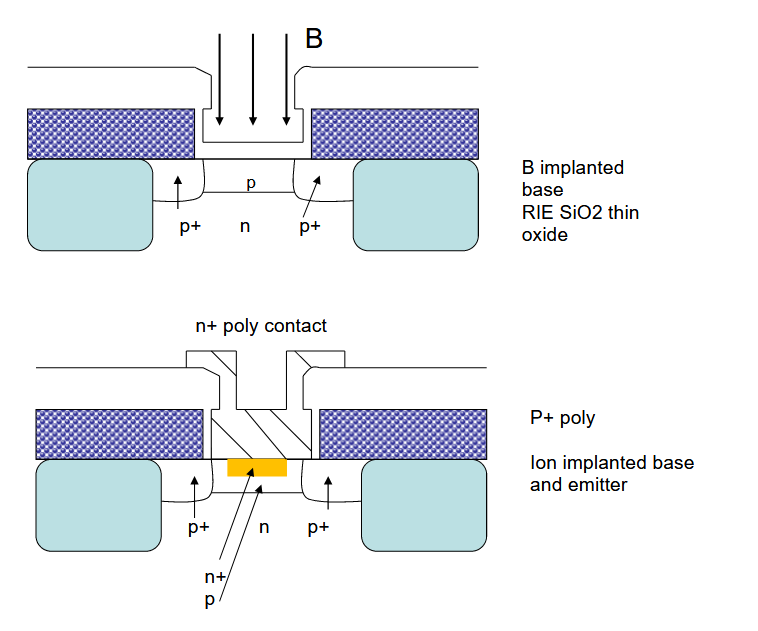
可以发现，用于接触的第二层多晶硅比发射极更宽。

5.3.6. 单多晶硅发射极制造

基极上的氧化物生长
发射极窗口掩蔽/蚀刻
硅表面清洁（HF 浸镀）
LPCVD 未掺杂多晶硅
将砷注入多晶硅
掺杂剂从多晶硅扩散到硅中

5.3.7. 硅-多晶硅界面的重要性

最重要的是要认识到增强的器件性能归因于硅-多晶硅界面。

界面质量：

多晶硅沉积之前的硅表面处理（蚀刻剂、时间）
多晶硅沉积条件影响晶粒生长
掺杂剂类型和退火条件（熔炉或 RTA）可影响多晶硅中的掺杂剂行为。
掺杂多晶硅的退火可能导致氧化层破裂和一些晶粒的外延重新排列。

5.4. 硅锗半导体合金

Si 和 Ge 可以在整个成分范围内形成随机合金。这种合金被写作。

之所以再使用 Ge，是因为通过在 Si 中添加 Ge，能够产生之间的能带间隙（这叫能带工程）。

材料	能带间隙	原子质量
Si
Ge

另一个原因是晶格常数。Ge 会比 Si 有更大的尺寸，所以尽管都是金刚石晶体结构，但是晶格常数不一样。并且由于晶格常数的差异，在 Si 上生长时会受到拉伸形变，由此会影响带隙。

5.5. 硅锗基双极晶体管

因为硼的浓度恒定，所以没有形成电场。电场都是 Ge 导致的。

Ge 浓度最高的点具有最窄的能带间隙。

所以掺杂 Ge 的目的就是使得基极中的分级带隙产生漂移电场，可以帮助少数载流子穿过基极。

5.5.1. 硅锗合金

将硅与锗制成合金也会使基极带隙变窄。

当带隙不均匀时（例如渐变的 Ge 分布），基础电场将会有一个额外的分量

5.6. SiGe 基极 BJT 的分析

5.6.1. 集电电流和增益

需要推导

5.6.2. 厄利电压

厄利电压大大增加了。

需要推导

也是能带变化导致的

🧩 ET Notes

探索

《Chapter 1 硅 BJT》笔记

1. 基础知识复习——BJT 和半导体物理

1.1. BJT

1.1.1. 点接触 BJT

点接触晶体管

1.1.1.1. 肖特基接触

肖特基接触

1.1.1.2. 欧姆接触

欧姆接触

势垒类型

特征量

1.1.2. BJT 结构

BJT 结构

1.1.3. BJT 工作模式

BJT 工作模式

工作模式感性认识

从能带进行分析

从 pn 结进行分析

1.1.4. BJT 基本工作原理

BJT 基本工作原理

1.1.5. BJT 特性

BJT 特性

高跨导

高截断频率

高电流负载

1.1.6. BJT 应用

BJT 应用

模拟

RF 微波

逻辑电路

开关

1.1.7. BJT 局限

BJT 局限

1.2. 半导体器件物理基础

1.2.1. 载流子浓度

1.2.1.1. 热平衡载流子浓度

导带电子热平衡浓度公式

价带空穴热平衡浓度公式

1.2.1.2. 状态密度函数

状态密度函数

一般模型

有效状态密度函数公式

半导体模型

导带底的电子状态密度

有效状态密度函数公式

价带顶的空穴状态密度

价带空穴状态密度函数计算式

1.2.1.3. 费米-狄拉克分布函数

费米-狄拉克分布函数

费米-狄拉克分布函数公式

特点

1.2.1.4. 本征载流子浓度

本征载流子浓度

计算公式

本征载流子浓度计算式

质量作用定律

1.2.2. 费米能级和准费米能级

1.2.2.1. 本征半导体的费米能级

本征费米能级

费米能级计算式

1.2.2.2. 非本征半导体的费米能级

非本征半导体的费米能级

N 型半导体费米能级计算式

P 型半导体费米能级计算式

1.2.2.3. 波尔兹曼关系

费米势定义式

波尔兹曼关系

1.2.2.4. 准费米能级

准费米能级

非热平衡电子浓度

非热平衡空穴浓度

准费米势能

1.2.3. 半导体中的电流

1.2.3.1. 漂移电流

电子漂移电流密度公式

空穴漂移电流密度公式

1.2.3.1.1. 迁移率

迁移率

2.7. 理想特性