为什么不直接跨越能带间隙进行复合

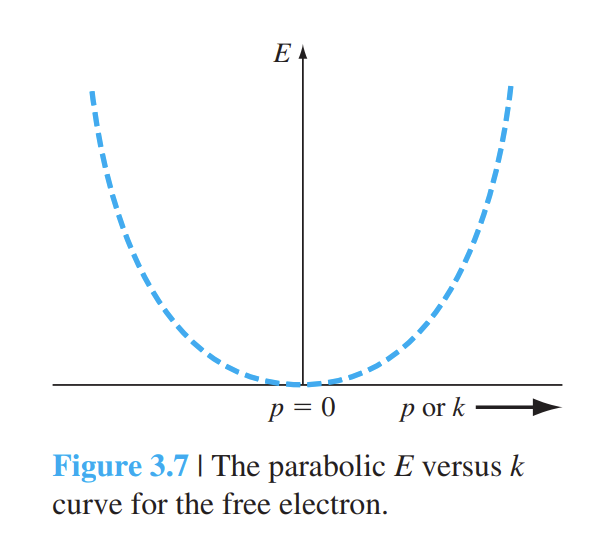
首先需要引入一个基本的内容，能量动量图，也叫 E-k 关系图。

自由粒子的 E-k 关系

为了更好地理解克龙尼克-潘纳模型，我们可以先考虑一个特殊情况，即没有势垒的自由粒子。

令 ，则有 以及，

由于势场为0，则总能量只含有动能,

然后我们将能量和动量联系起来，

E-k 动量公式

为约化普朗克常数； 为电子的波矢量； 为电子的有效质量

指向原始笔记的链接

得到自由电子的E-k关系如下图。

指向原始笔记的链接

对于空穴有效质量更大的直接带隙半导体而言，有如下的 E-k 关系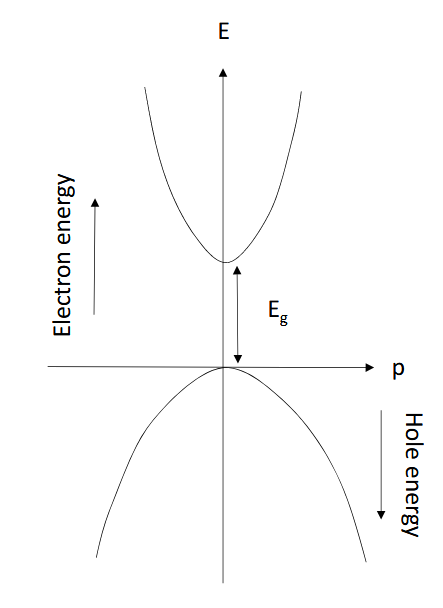， 可以看到，当电子的动量为 0 的时候，其处于导带底；空穴动量为 0 时，其处于价带顶。其之间的直接距离就是带隙。

但是对于非直接带隙半导体而言，其直接跨越能隙的复合是困难的，因为它涉及声子以守恒能量和动量。由于海森堡不确定性原理，复合中心可以帮助载流子复合。

坐标-动量不确定关系式

为约化普朗克常数

指向原始笔记的链接

通过减小坐标的不确定性从而增大动量的不确定性。因此，如果在能带间隙内一个复合中心，电子具有匹配动量矢量的概率会增加。