Important
注重物理而非数学,需要注重如何画好能带图。
期末试卷构成
分为 Part1(BJT)和 Part2(MOSFET):Q 1 (a),Q2 and Q3; Part3: Q1 (b) and Q4
[! tldr] Key Points of First class Vegard’s Law Critical thickness calculation band diagram constructure of HBT
1. 基础
异质结(heterostruction)被定义为由两种不同的半导体材料形成的结(结构)。此类半导体多为合金(化合物)半导体。
1.1. 合金半导体材料参数
采用物理的方式(例如 MBE)而非化学的方式形成合金。合金半导体是两种或多种半导体的组合,对于像
材料参数包括能带隙、晶格常数、热导率、熔点等。其中,带隙和晶格常数最为重要。
1.1.1. 维加德定律 Vegard’s Law
维加德定律是指对于三元化合物
其中 X 是摩尔分数或组成,可以在 0 到 1 之间变化。
1.1.1.1. 晶格常数
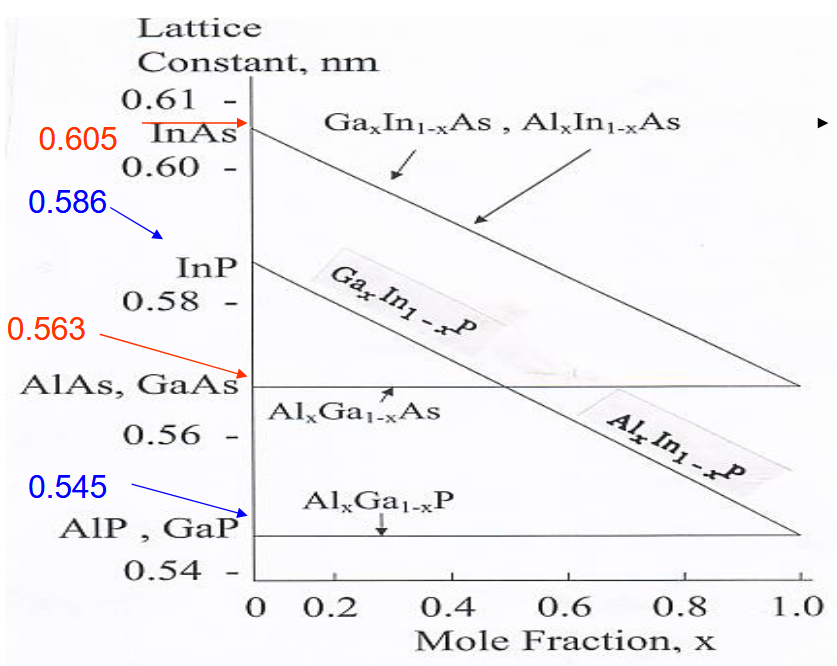 从这张图就可以看出,用不同或者相同晶格常数的元素进行替换的时候,合金晶格常数是如何变化的。
从这张图就可以看出,用不同或者相同晶格常数的元素进行替换的时候,合金晶格常数是如何变化的。
1.1.1.2. 能带间隙
三元和四元半导体的带隙仅大致遵循维加德定律。
在大多数合金中,由于不同元素的合金化而导致无序性增加,从而产生弯曲效应。合金半导体的能带隙可以用以下表达式更好地描述:
从一次关系变为了二次关系。
1.2. 晶格匹配和失配异质结构
异质结构有两种:
- 晶格匹配异质结构。这两种材料具有相同的晶格常数,例如: GaAs 上的 AlAs。
- 晶格失配异质结构。这两种材料具有不同的晶格常数,例如 GaAs 上的 InGaAs 和 Si 上的 SiGe。
晶格失配异质结构可进一步分为应变异质结构和非应变异质结构。
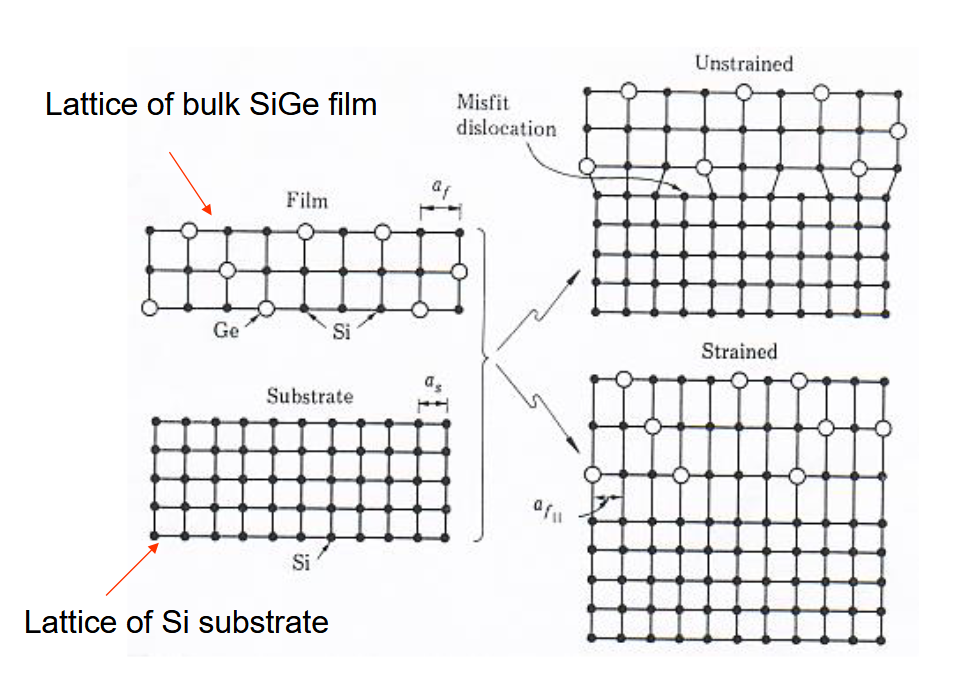
1.2.1. 应变异质结构
假设有,
为 衬底的晶格常数; 为 的晶格常数。
当外延生长的
由此定义平行于界面的应变为,
同理有垂直于界面的应变,
基底-薄膜晶格失配(或不适)定义为,
与平行应变相同。
1.2.2. 非应变异质结构
如果生长的 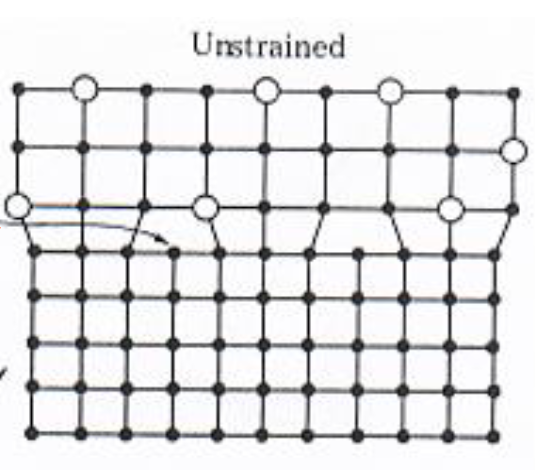 这导致在两种材料的界面处形成缺陷,称为失配位错。
这导致在两种材料的界面处形成缺陷,称为失配位错。
1.2.3. 临界厚度
存在一个临界厚度
1.3. 带隙不连续性
两种材料具有不同的能带隙。带缘结构可能分为三种类型:
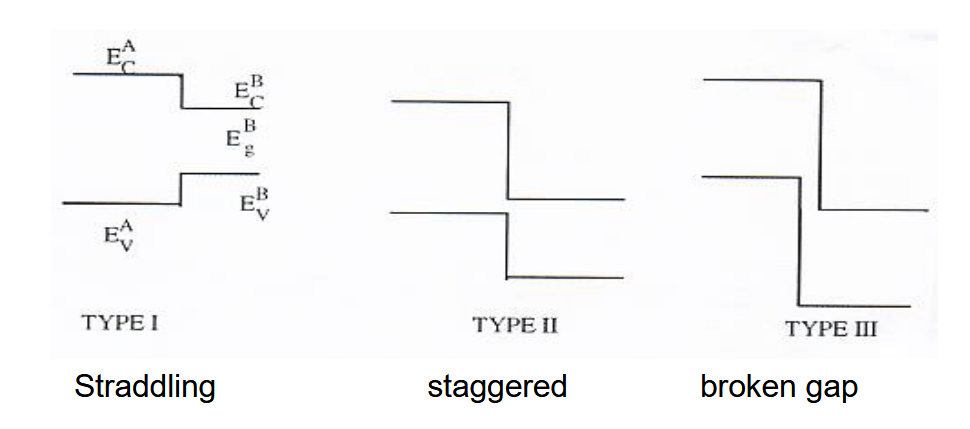 它们中的每一个都具有独特且特殊的能带结构和器件应用,我们主要关注第一种。
它们中的每一个都具有独特且特殊的能带结构和器件应用,我们主要关注第一种。
1.4. 异质结的能带图
- 先让真空能级平齐相接
- 随后电子从高费米能级流向低费米能级,失去电子的能带上弯,得到电子的能带下弯。
- 保持导带底能量差和价带顶能量差。
- 真空能级之间的差为内建电势。
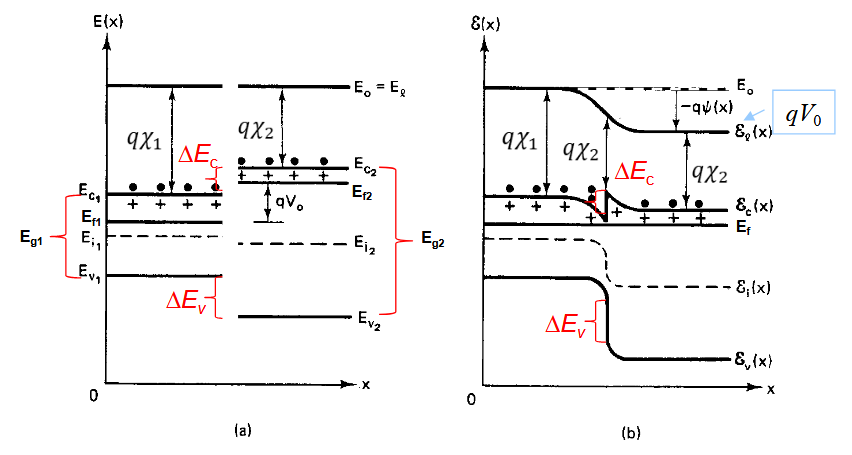
为什么不是金属的费米能级上升?
- 会导致真空能级的不连续
- 电子无法流动
[! note]
- 真空能级一定连续;
- 能带向上弯曲意味着电子能量增加,电子密度降低;
- 能带向下弯曲意味着电子能量减少,电子密度增加。
1.4.1. 带隙偏移
该比例随材料体系的不同而变化,不易确定。
1.4.2. 金属/
[! important] 可以拿这个能带图练一下手
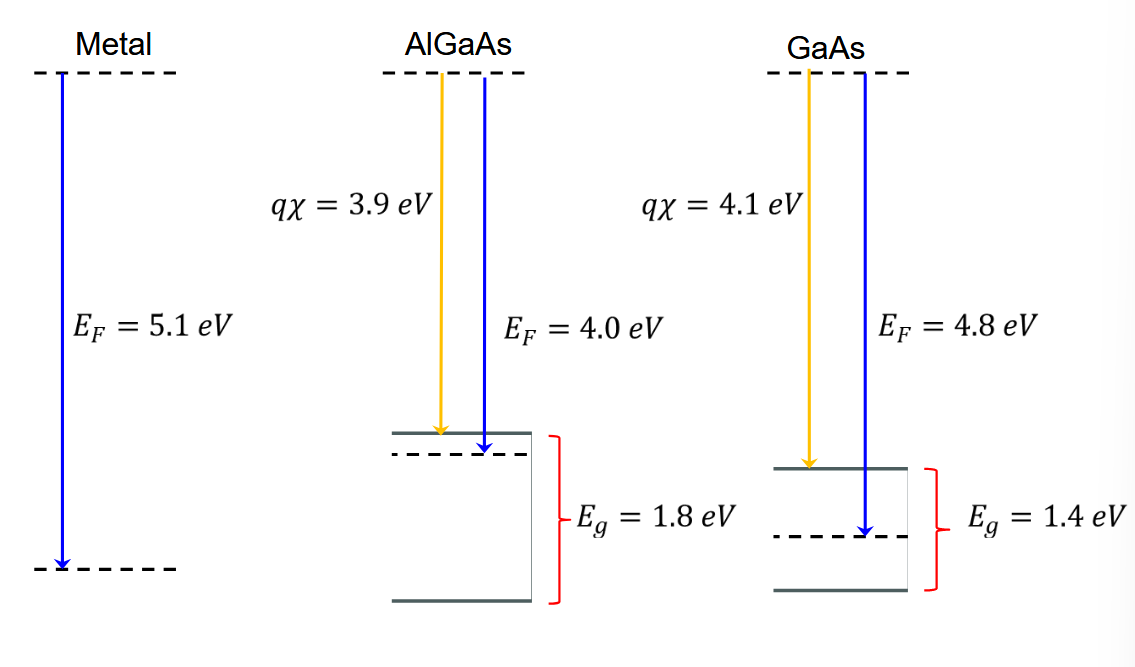
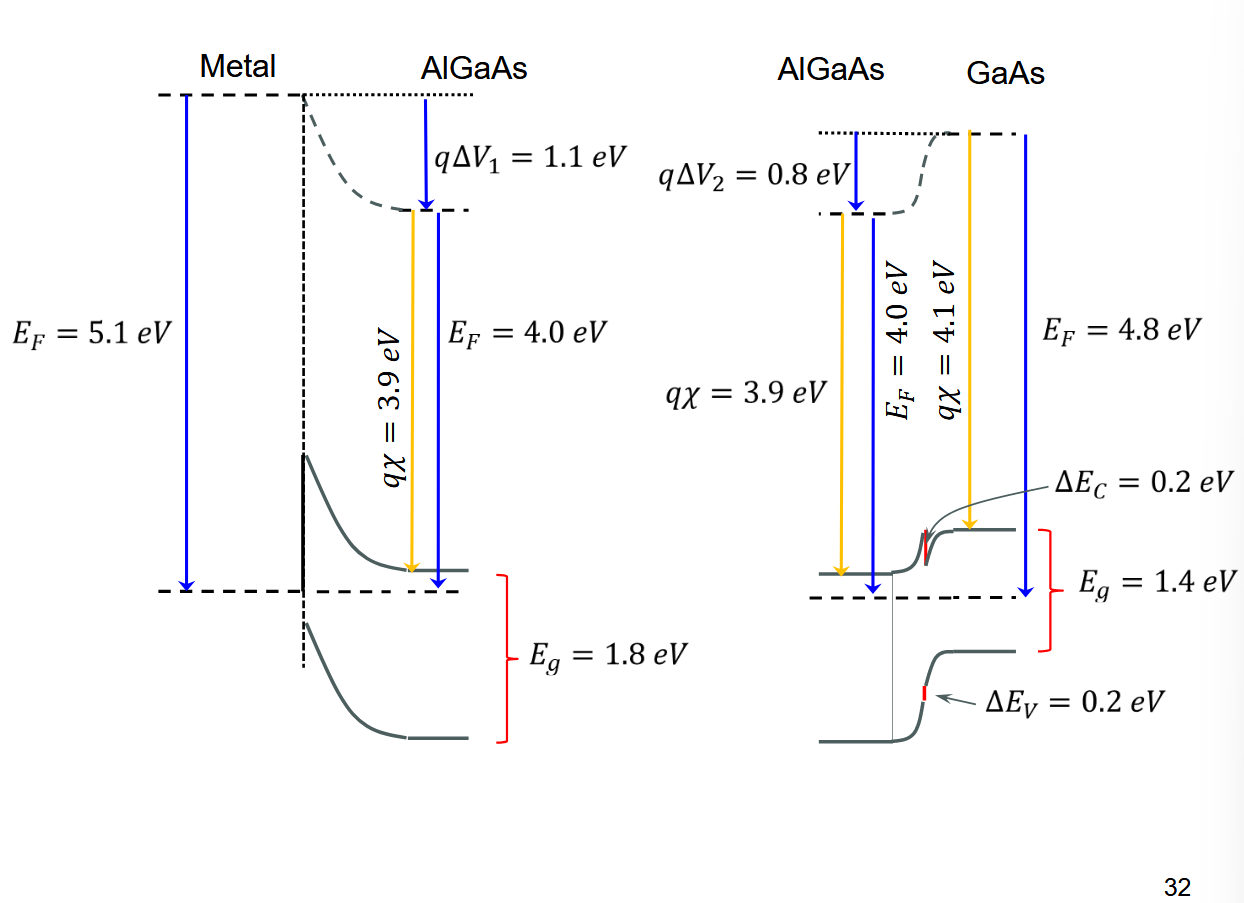
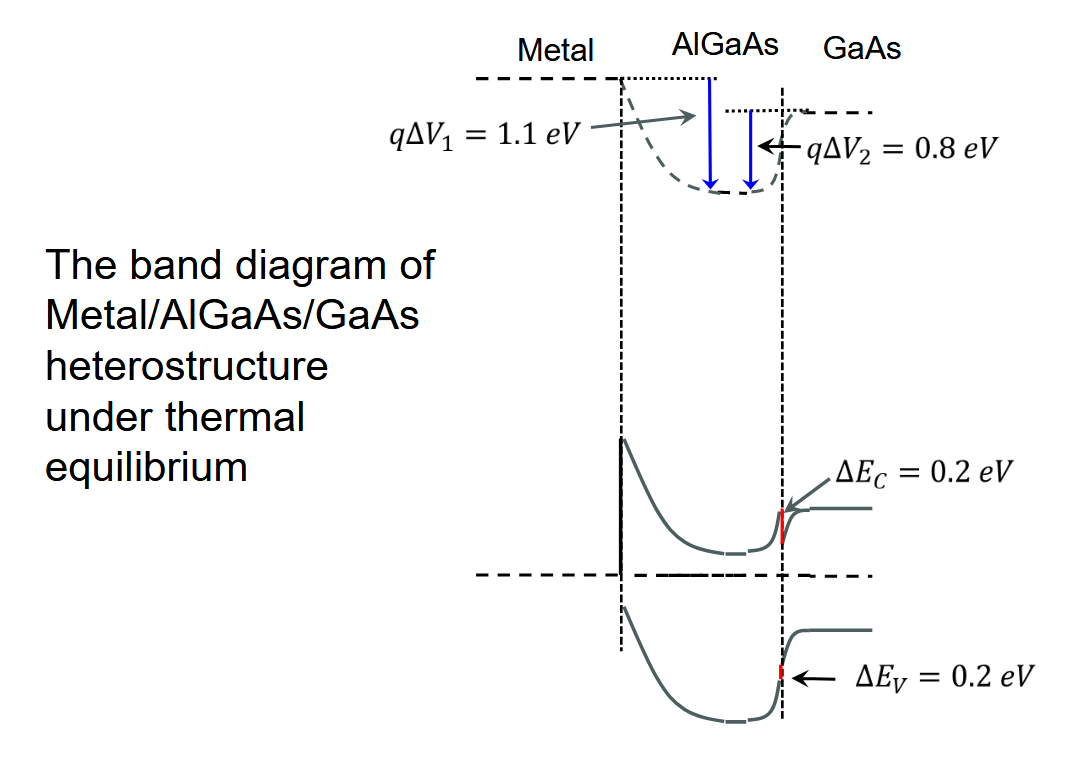
2. 异质结双极晶体管
[! reference] “4.5 异质结双极型晶体管” (施敏和李明逵, p. 147)
2.1. 同质结 BJT 的局限性
发射极注入效率为,
因为发射极注入效率定义式
指向原始笔记的链接
为基极 处的电子电流密度; 为基极 处的空穴电流密度
需要推导 从这个公式可以看出,如果想要增加发射极效率,那么发射极得重掺杂,基极得轻掺杂且尽量减小基区中性宽度。
基区输运系数
共基极电流增益
再代入共发射极增益
这里说明如果要 BJT 实现高增益,需要,
- 发射极重掺杂;
- 基极相对轻掺杂;
- 基极窄
但是如此又会导致问题,
- 发射极重掺杂会导致发射极带隙减小,从而减小发射极注入而增加基极注入,得不偿失 (重掺杂效应);
- 轻掺杂和窄基极会导致较大的基极电阻和更小的击穿电压。
2.2. 补救
主要的补救措施就是在 n 型发射极使用大带隙材料。该器件随后将成为异质结双极晶体管 (HBT)。
HBT 的主要优点是发射极效率高。HBT 还具有电路运行的高速和高频能力。
2.3. 基于 n-AlGaAs 和 p-GaAs 的 HBT
具有 n-AlGaAs 发射极和 p-GaAs 基极晶体管的 HBT
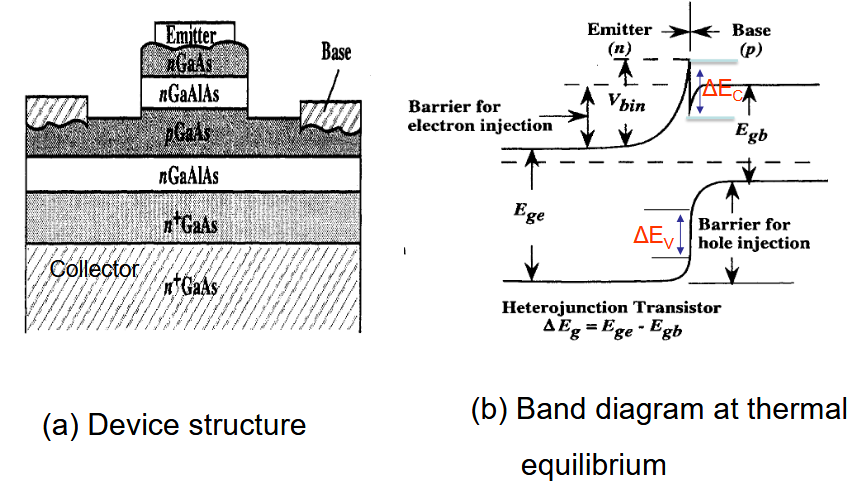
2.4. HBT 与同质结的对比
2021 #EE6604期末/2022
从 BJT 的共发射极增益再进一步推导,能看到
这意味着可以对基极进行大量掺杂并实现低基极电阻。还可以将基极做得更窄,以实现高速。因此,我们对高性能晶体管的所有要求都可以通过具有更大带隙发射极来满足。
2.5. 可用的结构
2.5.1. GaAs/AlGaAs HBT
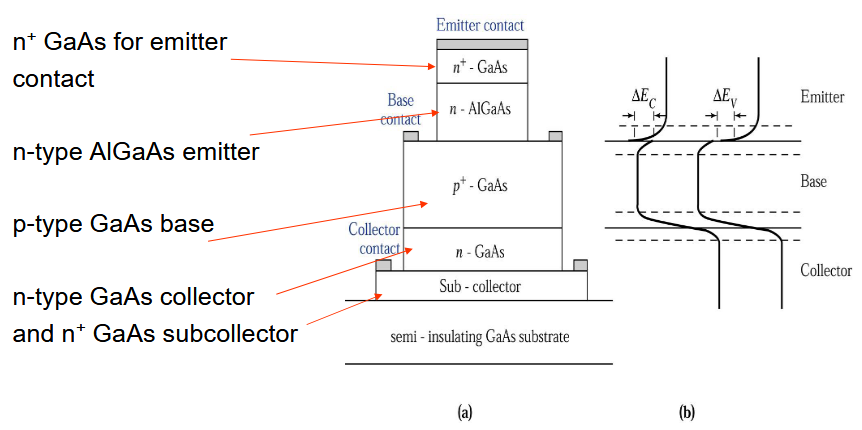
这个是一个基本的 HBT 结构,发射极由宽禁带的
2.5.2. InGaAs/InP 和 InGaAs/InAlAs HBT
优点在于:
- 非常低的表面复合;
- 比
更高的电子迁移率; 的截止频率; - 强电场下的更高电子漂移速度;
- 更高的击穿电压。
2.5.3.
优点在于,
- 禁带宽度差可实现基区重掺杂而具有高速能力;
- 表面复合电流少,低集电极电流的时候,电流增益仍然高。
2.6. 进一步提高 HBT 性能的途径
2021 #EE6604期末/2022
2.6.1. 发射极
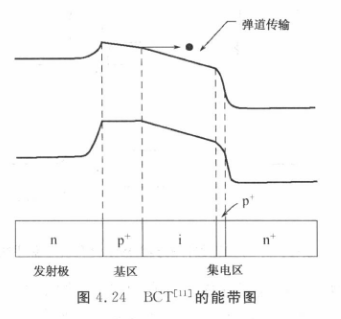
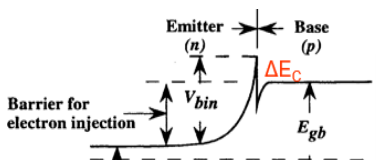 在发射极主要关注上图中的导带不连续,这会导致电子需要通过热发射或者隧穿才能到达基极,从而导致发射极效率降低或者集电极电流减小。
在发射极主要关注上图中的导带不连续,这会导致电子需要通过热发射或者隧穿才能到达基极,从而导致发射极效率降低或者集电极电流减小。
这个问题可以通过使用改进的结构来缓解,例如在 E-B 结附近使用具有渐变层的发射极。
2.6.2. 基极
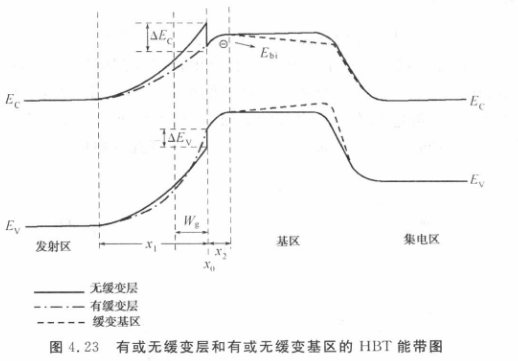
基区也可采用缓变分布, 使得基区的带隙由发射极一侧到集电极一侧逐步减小。存在一内建电场
2.6.3. 集电极
集电极我们主要考虑的是 集电区渡越时间和 击穿电压。采用特定的集电区掺杂,例如具有
3. 调制掺杂场效应晶体管 (MODFET)
MODFET 是异质结构的场效应器件。
3.1. 结构
MODFET 最有特点的结构在于栅极下方的异质结以及调制掺杂层。调制掺杂指的是,
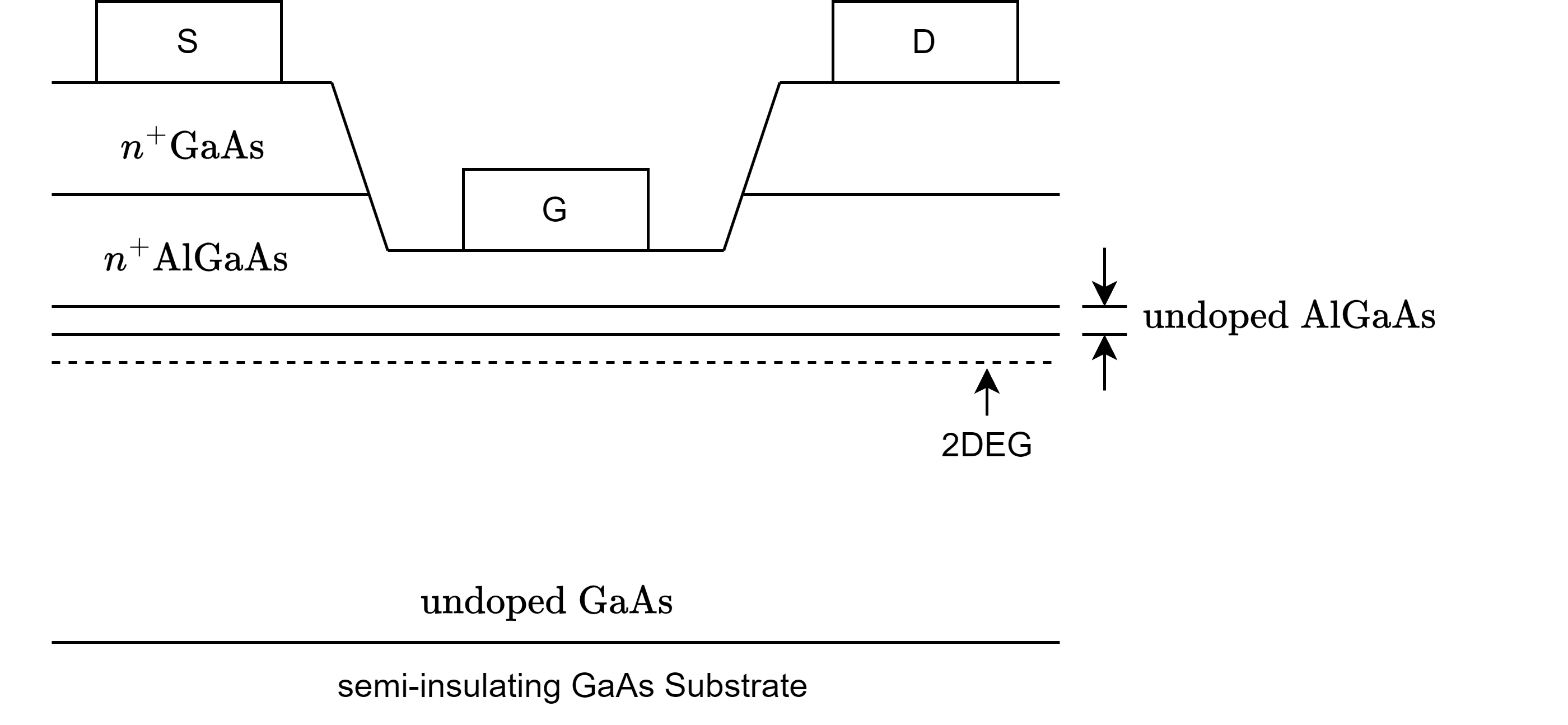
源和漏与
3.1.1. 迁移率随温度的变化
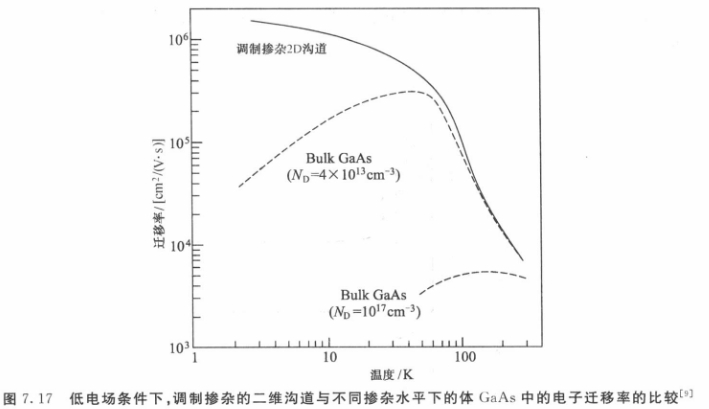 在低电场条件下,比较调制掺杂的 2D 沟道与不同掺杂水平下体
在低电场条件下,比较调制掺杂的 2D 沟道与不同掺杂水平下体
3.2. 能带分析
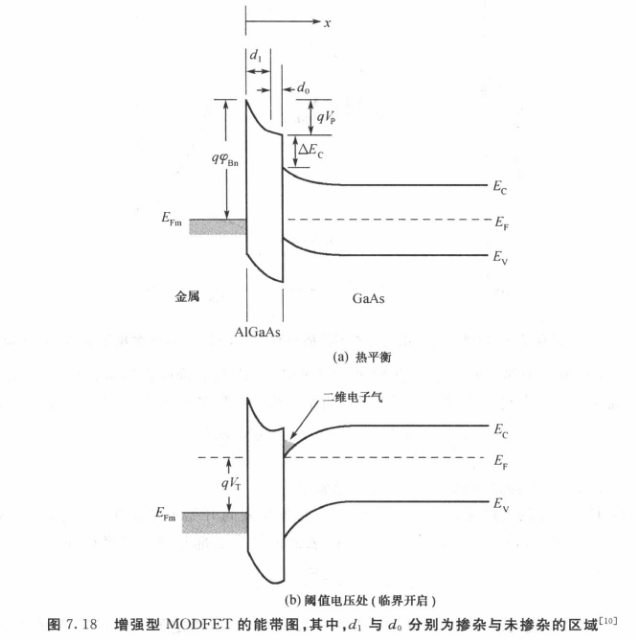 能带图中,
能带图中,
MODFET 的关键工作参数为阈值电压
当 MODFET 开启的时候,栅极在异质界面处容性感应出电荷薄层
3.3. 电流-电压分析
一般电流公式为,
当线性区的时候,有
在饱和区夹断的时候,令
在高速工作状态下,速度饱和区的电流为,
此时跨导为,