状态密度函数一般模型推导
状态密度函数一般模型讨论了一个被三维无限深势阱所束缚的电子。 我们将模型中的这个无限深势阱定义为
假设这个晶体是边长为
其中,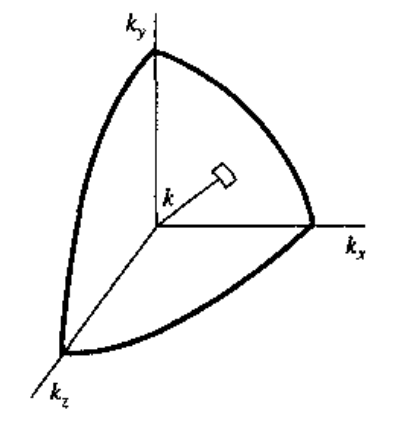
在
将其推广到三维,一个量子态所占据的空间
于是,我们可以确定
2 代表每个量子态的两种自旋状态;
我们也可以用能量
代入之后有
这个式子给出了体积为
状态密度函数一般模型讨论了一个被三维无限深势阱所束缚的电子。 我们将模型中的这个无限深势阱定义为
假设这个晶体是边长为
其中,
在
将其推广到三维,一个量子态所占据的空间
于是,我们可以确定
2 代表每个量子态的两种自旋状态;
我们也可以用能量
代入之后有
这个式子给出了体积为