第一章 数制和码制
第一章 数制和码制
1. 概述
数字电路所处理的各种数字信和号都是以数码形式给出的。不同的数码既可以用来表示不同数量的大小 ,又可以用来表示不同的事物或事物的不同状态。
数制
当数码用于表示数量大小的时候,多位数码中每一位的构成方法和从低位到高位的进位规则称为数制。
指向原始笔记的链接码制
码制是用不同数码表示不同事物或者事物不同状态时遵循的原则。
指向原始笔记的链接码制的分类
码制主要有以下分类:
指向原始笔记的链接2. 几种常用的数制
2.1. 十进制
十进制
在十进制数中,每一位有 0~9 十个数码,所以计数的基数是 10。超过 9 的数必须用多位数表示 , 其中低位和相邻高位之间的关系是「逢十进一」。
任意一个多位的十进制数
均可展开为, 任意一个多位的十进制数 D 的展开式
指向原始笔记的链接
是第 位系数,可以是 这 10 个数码中的任何一个;若整数部分的位数是 ,小数部分的位数为 ,则 包含从 到 的所有正整数和从 到 的所有负整数,整数部分的最高位为 ,最低位为 ;小数部分的最高位为 ,最低位为 。 一个 N 位的十进制数表示为
指向原始笔记的链接个数字中的某一个:0,1,2,3, , ,称为数的表示范围(range)。 如果用
取代上式中的 10,即可得到多位任意进制的( 进制)数展开式的普遍形式。 N 进制数展开式的普遍形式
指向原始笔记的链接
称为计数基数; 为第 的系数; 称为第 位的权。 2.2. 二进制
二进制
二进制和十进制一样,也是一种进位计数制,但是它的基数是 2,即逢二进一。每一位仅有
和 两种可能的数码。 二进制数的展开式
指向原始笔记的链接
为第 的系数; 称为第 位的权。 在二进制数中, 每一列的权 (从右到左) 分别为 1,2,4,8,16,32,64,128,256,512,1024,2048,4096,8192,16384,32768,65536,以此类推。如果你经常在二进制数下工作, 记住这些
指向原始笔记的链接会节省很多时间。 2.3. 八进制
八进制
八进制数的每一位有
八个不同的数码,计数的基数为 8。低位和相邻的高位之间的进位关系是“逢八进一”。任意一个八进制数可以展开为, 有时也用 O(Octal)来代替下脚注 8。指向原始笔记的链接八进制数展开式
指向原始笔记的链接
为第 位的系数 2.4. 十六进制
十六进制
十六进制数的每一位有十六个不同的数码,分别用
、A(10)、B(11)、C(12)、D(13)、E(14)、F(15)表示。因此,任意一个十六进制数均可展开为, 十六进制数展开式
指向原始笔记的链接
表示第 位的系数 有时也用 H(Hexadecimal)代替 16 这个脚注。
指向原始笔记的链接3. 不同数制之间的转换
不同数制间的转换
十进制转换成二进制
把一个十进制转换为二进制的方法是:把被转换的十进制数反复地除以 2,直到商为 0 为止,所得余数(从末位读起)就是这个数的二进制表示,简单地说,就是除 2 取余法。
二进制转十进制
要把二进制转换为十进制数,将二进制数按数的位置多项式表示法展开求和即可。
一个数的位置和多项式表示法
一个数的位置和多项式表示法
一个数用位置表示法表示为
「.」:radix point,小数点。在小数点之前的是整数位(integer digits),在其后的是小数位(fractional digits)。 「r」:radix base,称为底数或者进制。 「 」:是最高位(most significant digit, MSD) 「 」:是最低位(least significant digit, LSD) 其位置多项式可以表示为
指向原始笔记的链接二进制-十六进制
二进制转十六进制
由于 4 位二进制数恰好有 16 个状态,将 4 个二进制数看作一组,其进位输出又正好是逢十六进一。所以,只要从低位到高位将整数部分每 4 位二进制数分为一组,并代之以等值的十六进制数 ,同时从高位到低位将小数部分的每 4 位数分为一组,并代之以等值的十六进制数 ,即可得到对应的十六进制数。
当整数部分最高位一组不足 4 位时,用 0 补足 4 位;小数部分最低位不足 4 位时,用 0 补足 4 位。
指向原始笔记的链接十六进制转二进制
十六进制转二进制就是二进制转十六进制的逆过程。用 4 位二进制数替代十六进制的每一位就行。
八进制转二进制
八进制转二进制和二进制转八进制在方法上和二进制与十六进制互转相类似。通过使用 3 位二进制数就能替代一位八进制数。
十六进制与十进制的转换
十六进制转十进制的时候,将十六进制数展开相加即可。十进制转十六进制时,可先将其先转为二进制,然后转为十六进制。
指向原始笔记的链接4. 二进制算数运算
4.1. 二进制算术运算的特点
当两个二进制数码表示两个数量大小的时候,他们之间可以进行数值运算,这种运算称为算术运算,其规则和十进制运算基本相同。
二进制算术运算的两个特点 , 即二进制数的乘法运算可以通过若干次的“被乘数 (或零) 左移 1 位”和“被乘数 (或零) 与部分积相加”这两种操作完成;而二进制数的除法运算能通过若干次的“除数右移 1 位”和“从被除数或余数中减去除数”这两种操作完成。
4.2. 反码、补码和补码运算
为了在计算机中表示数字的正负,我们设计了原码。
在使用原码做减法的时候,整个流程十分麻烦,需要先比较绝对值大小,再做差然后再赋予符号。如果使用补码相加来代替整个做差的过程,就能简化电路。原码
原码
定义
原码是一种计算机中对数字的二进制定点表示法。原码表示法在数值前面增加了一位符号位(即最高位为符号位):正数该位为 0,负数该位为 1(0 有两种表示:+0 和 -0),其余位表示数值的大小。举个例子,我们用 8 位二进制表示一个数,+12 的原码为 00001100,-12 的原码就是 10001100。
指向原始笔记的链接在舍弃进位的条件下 , 减去某个数可以用加上它的补码来代替。这个结论同样适用于二进制数的运算。补码
补码是一种用二进制表示有符号数的方法。正数和 0 的补码就是该数字本身。负数的补码则是将其对应正数按位取反再加 1。
指向原始笔记的链接补码的出现是为了解决原码和反码所带了的两个问题:
- 正负数相加不等于 0
- 0 有两种表现形式
补码的表示方法如下,
为了避免求补码的时候做减法运算,通常先求出二进制数的补码表示方法
对于有效数字(不包括符号位)为
位的二进制数 ,其补码 为, 指向原始笔记的链接 的反码 ,然后在复数的反码上加 1 得到补码。二进制数的反码定义如下, 二进制数的反码表示方法
对于有效数字(不包括符号位)为
位的二进制数 ,其反码 为, 指向原始笔记的链接 反码
反码是一种在计算机中数的机器码表示。对于单个数值(二进制的 0 和 1)而言,对其进行取反操作就是将 0 变为 1,1 变为 0。正数的反码和原码一样,负数的反码就是在原码的基础上符号位保持不变,其他位取反。
十进制 原码 反码 6 0000 0110 0000 0110 -3 1000 0011 1111 1100 反码使得计算机在进行运算时可以不用去管符号位,也就是让符号位参与运算。
指向原始笔记的链接根据上面两个公式可以知道,当二进制数
为负数的时候,其补码为, 二进制负数的补码计算式
指向原始笔记的链接 5. 几种常用的编码
5.1. 十进制代码
指向原始笔记的链接十进制代码
十进制代码
概念
十进制代码是为了用二进制代码表示十进制数的 0-9 这十个状态而创造的一种等长编码。
几种常见的十进制代码
[
]
- 8421 码
- 又称为 BCD (Binary Coded Decimal) 码,是十进制代码中最常用的一种。每一位的 1 代表的十进制数称为这一位的权。8421 码中每一位的权是固定不变的,它属于有权码。
- 余 3 码
- 编码规则与 8421 码不同。如果将两个余 3 码相加,所得的和将比十进制数和所对应的二进制数多 6。0 和 9、1 和 8、2 和 7、3 和 6、4 和 5 的余 3 码互为反码,这对于求取对 10 的补码是很方便的。余 3 码不是恒权码。
- 2421 码
- 一种恒权码,它的 0 和 9、1 和 8、2 和 7、3 和 6、4 和 5 也互为反码。
- 5211 码
- 是另一种恒权码。5211 码的每一位正好与 8421 码十进制计数器 4 个触发器输出脉冲的分频比相对应。这种对应关系在构成某些数字系统时很有用。
- 余 3 循环码
- 是一种无权码,每一位的 1 在不同代码中并不代表固定的数值。它的主要特点是相邻的两个代码之间仅有一位的状态不同。
- 格雷码
指向原始笔记的链接笔记来源
第二章 逻辑代数基础
第二章 逻辑代数基础
1. 逻辑代数中的三种基本运算
逻辑代数的三种基本运算
逻辑代数的三种基本运算包括逻辑“与”、逻辑“或”、逻辑“非”
逻辑“与”
逻辑“与”
逻辑“与”通常也用
指向原始笔记的链接来表示。需要两个或多个条件同时成立才为 1 逻辑“或”
逻辑“或”
逻辑“或”通常也用“OR”表示。其意味着条件之一具备,结果就发生。
真值表
A B y 0 0 0 0 1 1 1 0 1 1 1 1 逻辑“非”
指向原始笔记的链接逻辑“非”
逻辑“非”通常也用
指向原始笔记的链接表示 常用的一些复合运算逻辑,
2. 逻辑代数的基本公式和常用公式
逻辑代数公式
逻辑代数的基本公式
公式说明 公式 1 公式 2 1 2 重叠律 互补律 交换律 结合律 分配律 反演律(德摩根定理) 还原律 10 ; 11 12 逻辑代数的常用公式
指向原始笔记的链接
序号 公式 21 22 23 24 25
26
3. 逻辑代数的基本定理
逻辑代数基本定理
代入定理
代入定理
代入定理指,在任何一个包含
指向原始笔记的链接的逻辑等式中,若以另外一个逻辑式代入式中 的位置,则等式依然成立。因为逻辑式和 A 均只有 0 和 1 两种取值,因此代入定理可以被看为是无需证明的公理。 反演定理
反演定理
对于任何一个逻辑式
,若将其中的所有“ ”换为 “ ”,所有“ ”换为 “ ”,0 换成 1,1 换成 0,原变量换成反变量,反变量换成原变量,得到的结果就是 。这个规律就是反演定理。 反演定理可以用于求取已知逻辑式的反逻辑式。
在使用反演定理的时候,需要遵守以下两个守则,
指向原始笔记的链接
- 仍需遵守“先括号、然后乘、最后加”的运算优先次序;
- 不属于单个变量上的反号应保留不变。
对偶定理
指向原始笔记的链接对偶定理
若两逻辑式相等,则它们的对偶式也相等,这就是对偶定理。
所谓对偶式是这样定义的:对于任何一个逻辑式
, 若将其中的“ ”换成“ ”,“ ”换成“ ”, 0 换成 1,1 换成 0,则得到一个新的逻辑式 , 这个 就称为 的对偶式,或者说 和 互为对偶式。 为了证明两个逻辑式相等,也可以通过证明它们的对偶式相等来完成,因为有些情况下证明它们的对偶式相等更加容易。
指向原始笔记的链接4. 逻辑函数及其描述方法
4.1. 逻辑函数
逻辑函数
若以逻辑变量为输入,运算结果为输出,则输入变量值确定以后,输出的取值也随之而定。输入与输出之间是一种函数关系。这种函数关系称为逻辑函数,写作,
注:在二值逻辑中,输入与输出都只有两种取值 0 和1。
指向原始笔记的链接4.2. 逻辑函数的表示方法
逻辑函数的表示方法
逻辑真值表
逻辑真值表
真值表的左边列出输入,右边列出输出,每种可能的输入组合对应一行。
指向原始笔记的链接逻辑函数式
逻辑函数式
逻辑函数式将输入与输出之间的逻辑关系用与、或、非的运算式表示就得到逻辑式。
指向原始笔记的链接 逻辑图
逻辑图
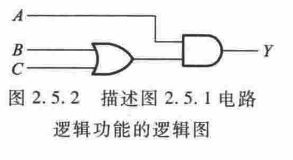
逻辑图将逻辑函数式中的各变量之间的与、或、非等逻辑关系,用对应的逻辑图形符号表示出来,就能画出描述函数关系的逻辑图。
指向原始笔记的链接波形图
波形图
波形图将输入变量所有取值可能与对应输出按时间顺序排列起来画成时间波形。这种波形图也叫做时序图。
指向原始笔记的链接卡诺图
卡诺图
卡诺图是将逻辑函数的最小项之和的以图形的方式表示出来。用「1」表示最小项存在,「d」既可以当作「0」,也可以当作「1」。
原则
以
个小方块分别代表 变量的所有最小项,并将它们排列成矩阵,而且使几何位置相邻的两个最小项在逻辑上也是相邻的(只有一个变量不同),就得到表示 变量全部最小项的卡诺图。
化简特性(卡诺图化简法)
指向原始笔记的链接
- 卡诺图中两个相邻 1 格的最小项可以合并成一个与项,并消去一个变量。
- 卡诺图中四个相邻 1 格的最小项可以合并成一个与项,并消去两个变量。
- 卡诺图中八个相邻 1 格的最小项可以合并成一个与项,并消去三个变量。
EDA 中硬件描述语言(HDL)
指向原始笔记的链接4.3. 逻辑函数表达方法之间的转换
逻辑函数表达方法之间的转换
真值表与逻辑式
真值表-逻辑式-转换
真值表到逻辑函数式
- 找出真值表中使逻辑函数
的那些输人变量取值的组合。 - 每组输人变量取值的组合对应一个乘积项,其中取值为 1 的写人原变量,取值为 0 的写 入反变量。
- 将这些乘积项相加,即得
的逻辑函数式。 逻辑函数式到真值表
由逻辑式列出真值表就更简单了。这时只需将输人变量取值的所有组合状态逐一代人逻辑 式求出函数值,列成表,即可得到真值表。
指向原始笔记的链接逻辑函数式与逻辑图
逻辑式-逻辑图-转换
指向原始笔记的链接
- 用图形符号代替逻辑式中的逻辑运算符。
- 从输入到输出逐级写出每个图形符号对应的逻辑运算式。
波形图与真值表
指向原始笔记的链接波形图与真值表的转换
在从已知的逻辑函数波形图求对应的真值表时,首先需要从波形图上找出每个时间段里输入变量与函数输出的取值,然后将这些输入、输出取值对应列表,就得到了所求的真值表。
在将真值表转换为波形图时,只需将真值表中所有的输人变量与对应的输出变量取值依次排列画成以时间为横轴的波形,就得到了所求的波形图,如我们前面已经做过的那样。
指向原始笔记的链接4.4. 逻辑函数的两种标准形式
逻辑函数的两种标准形式
逻辑函数有「最小项之和」和「最大项之积」两种标准形式。首先说明最小项和最大项的概念。
最小项和最大项
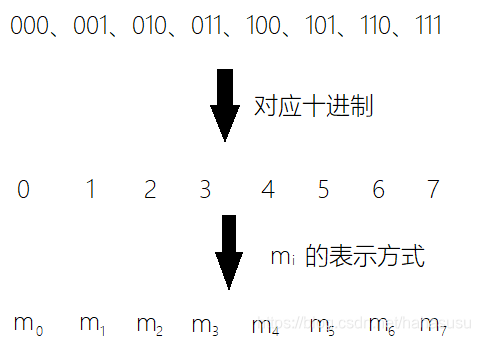
最小项
对于
个因子,其最小项 :
是乘积项 - 包含
个因子 个变量均以原变量和反变量的形式在 中出现一次 - 总共有
个
性质
指向原始笔记的链接
- 在输入变量任一取值下,有且仅有一个最小项的值为 1
- 全体最小项之和为 1
- 任何两个最小项之积为 0
- 最小项具有相邻性
- 任何两个最小项如果他们只有一个因子不同,其余因子都相同,则称这两个最小项为相邻最小项。
- 两个相邻的最小项之和可以合并,消去一对因子,只留下公共因子
最大项
在
变量逻辑函数中,若 为 个变量之和,而且这 个变量均以原变量或反变量的形式在 中出现一次,则称 为该组变量的最大项。 性质
指向原始笔记的链接最小项之和形式
最小项之和
首先将给定的逻辑函数式化为若干乘积项之和的形式(亦称“积之和”形式), 然后再利用基本公式
将每个乘积项中缺少的因子补全, 这样就可以将与或的形式化为最小项之和的标准形式。 转换
最小项之和与最大项之积的关系为
最小项之和可以转化为对应项的最大项之积。
指向原始笔记的链接笔记来源
最大项之积形式
指向原始笔记的链接最大项之积
利用逻辑代数的基本公式和原理, 首先我们一定能把任何一个逻辑函数式化成若干项相乘的或与形式(也称“和之积”形式). 然后再利用公式
将每个多项式中缺少的变量补齐, 就可以将函数式的或与形式化成最大项之积的形式了. 指向原始笔记的链接笔记来源
5. 逻辑函数的化简方法
逻辑函数的化简方法
逻辑式越简单,其所表示的逻辑关系越明显,同时也有利于用最少的电子器件来实现这个逻辑函数,因此需要通过化简来找到最简形式。
逻辑函数的最简形式
当函数式中包含的乘积项最少,且乘积式里的因子也不能减少的时候,此逻辑式为最简逻辑式。
指向原始笔记的链接1. 公式化简法
公式化简法就是反复使用逻辑代数的基本公式和常用公式去消去函数式中多余的乘积项和多余的因子,没有固定步骤。
1.1. 并项法
利用逻辑代数公式中的
就能将两项合并为一项。 1.2. 吸收法
利用逻辑代数公式中的
,将 AB 项消去。 1.3. 消项法
利用公式
以及 将 或者 项消去。 1.4. 消因子法
利用公式
将 中的 消去。 1.5. 配项法
- 根据公式中的
可以在逻辑函数式中重复写入某一项, 有时能获得更加简单的化简结果。 - 根据基本公式中的
可以在函数式中的某一项上乘以 , 拆然成两后项分别与其他项合并 ,有时能得到更加简单的化简结果。 2. 卡诺图化简法
由于任何逻辑函数都可以展开为最小项之和的形式,可以采用合并最小项的方法化简逻辑函数。这种方法是适用于任何逻辑函数的、通用的化简方法。
指向原始笔记的链接6.
指向原始笔记的链接
第三章 门电路
Transclude of 第三章-门电路
第四章 组合逻辑电路
第四章 组合逻辑电路
[! tldr] 本章将重点介绍组合逻辑电路的特点以及组合逻辑电路的分析方法和设计方法。首先讲述组合逻辑电路的共同特点和一般的分析方法和设计方法。然后就几种常用且经典的组合逻辑电路模块 ,从分析或设计的角度进行解读 ,并在模的块基础上 ,初步介绍如何用硬件描述语言描述组合逻辑电路。最后着重从物理概念上说明竞争 -冒险现象及其成因 ,并扼要地介绍消除竞争 -冒险现象的常用方法。
1. 概述
1.1. 组合逻辑电路的特点
数字电路根据逻辑功能的不同,可以分为两大类,组合逻辑电路和时序逻辑电路
组合逻辑电路的特点
在组合逻辑电路中,任意时刻的输出仅仅取决于该时刻的输入和逻辑电路本身的结构,与电路原来的状态无关。这就是组合逻辑电路在逻辑功能上的共同特点。
指向原始笔记的链接
1.2. 逻辑功能的描述
逻辑功能的描述
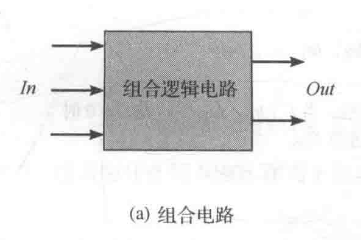
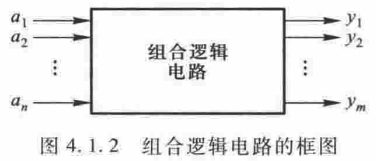
对于任何一个多输入、多输出的组合逻辑电路,都可以用下面的框图表示。
输入变量
和输出变量 的逻辑关系可以用一组逻辑函数表示, 或者写成向量函数的形式,
除了逻辑式之外,还有真值表、逻辑图、波形图等。
在设计和实现中,还需要对其动态参数—— 传输延迟时间
指向原始笔记的链接进行描述。 2. 组合逻辑的分析方法
组合逻辑的分析方法
通常采用的分析方法是从电路的输入到输出逐级写出逻辑函数式,最后得到表示输出与输人关系的逻辑函数式。然后用公式化简法或卡诺图化简法将得到的函数式化简或变换, 以使逻辑关系简单明了。为了使电路的逻辑功能更加直观,有时还可以将逻辑函数式转换为真值表的形式。
从电路图也可分析出该电路最重要的动态参数——传输延迟时间。假定每个门电路的传输延迟时间是
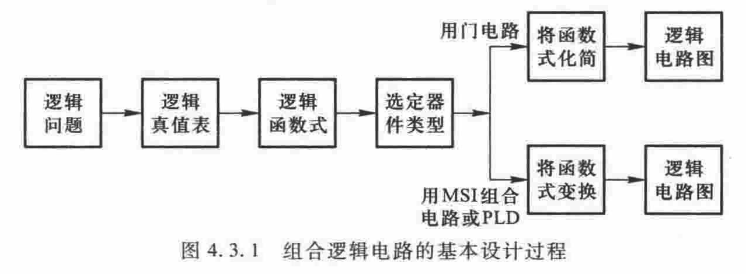
指向原始笔记的链接,则整个电路的传输延迟时间是 。 3. 组合逻辑电路的基本设计方法
组合电路的基本设计方法
在设计组合电路的时候,通常要求电路最简,即使用器件数少、器件种类少以及器件间连线最少。
1. 进行逻辑抽象
- 分析因果,确定输入和输出;
- 对输入变量和输出变量进行二进制编码;
- 对给定的因果关系列出真值表。
2. 写出逻辑函数式
将真值表转换为逻辑函数式,见第二章的真值表与逻辑函数式的相互转换。
3. 选定器件类型
可以用不同集成度的数字电路来实现功能。应该根据对电路的具体要求和器件的资源情况决定采用哪一种类型的器件。
4. 将逻辑函数化简或转换成适当的描述形式
在使用小规模集成的逻辑门电路进行电路实现时,为获得最简单的设计结果,应将函数式化成最简形式,即函数式相加的乘积项最少,而且每个乘积项中的因子也最少。
如果对所用器件的种类有附加的限制(例如只允许用单一类型的与非门),则还应将函数式变换成与器件种类相适应的形式(例如将函数式化作与非-与非形式)。
5. 根据化简或转换后的逻辑式,画出逻辑电路的连接图
至此 ,原性理设计(或称逻辑设计)已经完成。
6. 设计验证
对已经得到的原理图进行分析,或借助计算机仿真软件进行功能和动态特性仿真,验证其是否符合设计要求。
7. 工艺设计
为了将逻辑电路实现为具体的电路装置,还需要做一系列的工艺设计工作,包括设计印刷电路板,机箱面板,电源,显示电路等。最后还必须完成组装,调试。
指向原始笔记的链接
4. 若干常用的组合逻辑电路模块
有些逻辑功能电路经常大量地出现在各种数字系统当中,包括编码器、译码器、数据选择器、数值比较器运算器等。在设计实现复杂的电路时,可以调用这些已有的、经过使用验证的电路模块,作为设计电路的组成部分。
4.1. 编码器
编码器的逻辑功能在于将输入的每一个高、低电平信号编成一个对应的二进制代码。
目前经常使用的编码器有普通编码器和优先编码器两种。
4.1.1. 普通编码器
普通编码器
普通编码器中,任何时刻只允许输入一个编码信号,否则输出将发生混乱。
指向原始笔记的链接4.1.2. 优先编码器
优先编码器
在优先编码器(priority encoder)电路中,允许同时输入两个以上的编码信号。不过在设计优先编码器时已经将所有的输入信号按优先顺序排了队,当几个输入信号同时出现时,只对其中优先权最高的一个进行编码。
指向原始笔记的链接[! question] 如何实现对输入信号的优先级进行限制的?
4.2. 译码器
码器 (decoder)的逻辑功能是将每个输入的二进制代码译成对应的输出高、低电平信号或另一外个代码。因此译码是编码的反操作。常用的译码器电路有二进制译码器、二-十进制译码器和显示译码器三类。
4.2.1. 二进制译码器
二进制译码器
二进制译码器的输入是一组二进制代码,输出是一组与输入代一码一一对应的高、低电平信号。
指向原始笔记的链接4.2.2. 二-十进制译码器
二-十进制译码器
二-十进制译码器的逻辑功能是将输入 BCD 码的 10 个代码译成 10 个高、低电平输出信号。
对于 BCD 代以外码的伪码 ( 即
指向原始笔记的链接这 6 个代码 ) 均无低电平信号产生,译码器拒绝“翻译”。所以这个电路结构具有拒绝伪码的功能。 4.2.3. 显示译码器
显示译码器
七段字符显示器
指向原始笔记的链接4.3. 数据选择器
4.4. 加法器
两个二进制数之间的算术运算无论是加、减、乘、除,目前在数字计算机中都是化做若干步加法运算进行的。因此,加法器是构成算术运算器的基本单元。
4.4.1. 1 位加法器
1 位加法器
半加器
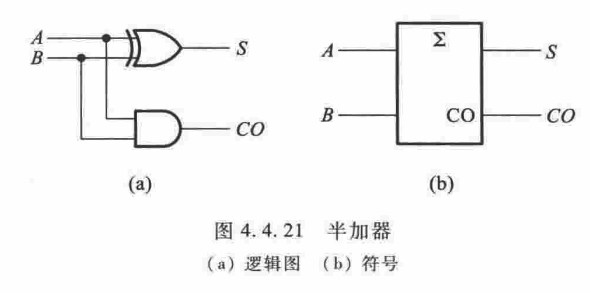
半加器
如果不考虑有来自低位的进位,将两个 1 位二进制数相加,称为半加。实现半加运算的电路称为半加器。
有逻辑表达式为,
半加器使用一个异或门和一个与门即可实现。
指向原始笔记的链接全加器
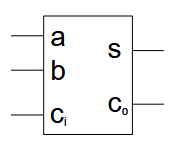
指向原始笔记的链接全加器
将两个对应位的加数和来自低位的进位 3 个数相加,并输出一个和以及一个进位。这种运算称为全加,所用的电路称为全加器。
有逻辑式为,
指向原始笔记的链接
4.4.2. 多位加法器
多位加法器
串行进位加法器
串行进位加法器
两个多位数相加时每一位都是带进位相加的,因而必须使用全加器。
只要依次将低位全加器的进位输出端接在高位全加器的进位输入端即可构成。其缺点在于计算是串行的,计算速度慢。
指向原始笔记的链接超前进位加法器
指向原始笔记的链接超前进位加法器
我们知道,加到第
位的进位输人信号是这两个加数第 位以下各位状态的函数,所以第 位的进位输入信号 一定能由 和 唯一地确定。根据这个原理,就可以通过逻辑电路事先得出每一位全加器的进位输人信号,而无需再从最低位开始向高位逐位传。 相当于是用复杂度换计算速度,即通过逻辑函数将第
指向原始笔记的链接位是否需要进位判断出来。 4.5. 数值比较器
4.5.1. 位数值比较器
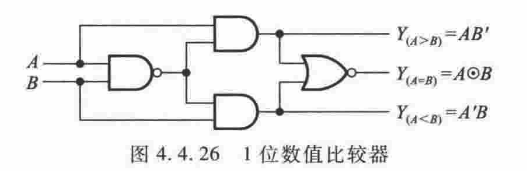
1 位数值比较器
当只有 1 位的时候,有三种情况,
指向原始笔记的链接
4.5.2. 多位数值比较器
多位数值比较器
比较两个多位数时,需要从高位往下比。
指向原始笔记的链接5. 层次化和模块化的设计方法
层次化的设计方法是指“自顶向下”对整个设计任务进行分层和分块的划分,降低每层的复杂度,简化每个模块的功能;或“自底向上”地对每一个有限复杂度的模块进行实现或调用。模块化的设计方法是指将经过设计和验证的能完成一定功能的逻辑电路封装成为模块,在后续的设计中都可反复使用。
其核心都是将复杂电路逐级分解成简单模块,然后再将模块设计好并连接起来。
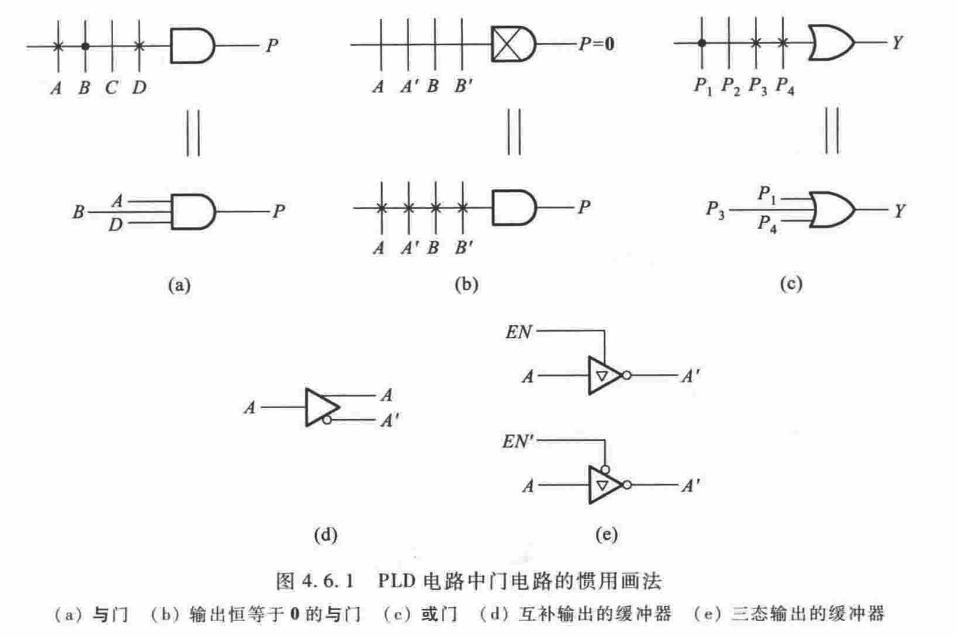
6. 可编程逻辑器件
从逻辑功能上,又能将数字集成电路分为通用型和专有型。
可编程逻辑器件(Programming Logic Device, PLD)的研制使得能通过器件编程来设定逻辑功能。能够由设计人员自行编程去将一个数字系统“集成”到一片 PLD 上,做成片上系统(System On Chip, SoC)。
7. 硬件描述语言
硬件描述语言 (HDL) 就是设计人员利用 EDA 工具描述电子电路的一种方法。利用硬件描述语言并借助 EDA 工具,可以完成从系统、算法、协议的抽象层次对电路进行建模、电路的仿真、性能分析直到 IC 版图或 PCB 版图生成的全部设计工作。
针对数字电子电路 ,硬件描述语言可以在不同的层次对结构,功能和行为进行描述。常见的硬件描述语言包括 Verilog、VHDL 等
Transclude of Verilog-基础8. 用可编程通用模块设计组合电路
9. 组合逻辑电路中的竞争-冒险
需要观察输入信号逻辑电平发生变化的瞬间,电路的工作情况。
9.1. 竞争-冒险现象及其成因
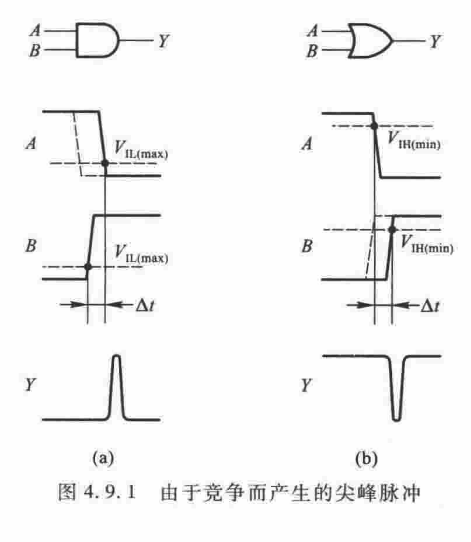
拿(a)的与门举例。当输入信号 A 从 1 跳变到 0,同时 B 从 0 跳变到 1,而且 B 首先上升到
以上。在极短的时间 内,将出现 A、B 同时高于 的情况,输出出现极窄的 的尖峰脉冲,也叫电压毛刺,是一种系统内部的噪声。 我们将门电路两个输入信和号同时向相反的逻辑电平跳变(一个从 1 变为 0,另一个从 0 变为 1)的现象称为竞争。竞争不一定产生尖峰脉冲。
由于竞争而在电路输出端可能产生尖峰脉冲的现象就称为竞争-冒险。
9.2. 检查竞争-冒险的方法
在输入变量每次只有一个改变状态的简单情况下,可以通过逻辑函数式来判断。
如果输出端门电路的两个输入信号
和 是输入变量 经过两个不同的传输途径而来的,那当输么入变量 的状态发生突变时输出端便有可能产生尖峰脉冲。 即输出端能在一定条件下简化为,
(或门输出), (与门输出), (或非门输出), (与非门输出)。 这种方法简单,但是局限性大。因为大多数情况的输入变量都有两个以上同时改变状态,如果输入变量增多,更难从逻辑函数式上找出。
另一类方法即用实验的手段来检测尖峰脉冲,通过加到输入端的信号波形包括所有可能发生的情况。
9.3. 消除竞争-冒险的方法
9.3.1. 接入滤波电容
因为一般的因为竞争-冒险产生的尖峰脉冲都很窄,通过引入滤波电容就能削弱至门电路的阈值以下。这种方法简单易行,缺点是增加了输出电压波形的上升和下降时间。
9.3.2. 引入选通脉冲
为的高电平出现在电路到达稳定状态以后 , 所以 G u ~ G ; 每个门的输出端都不会出现尖峰脉冲。但需注意 , 这时 G u ~ G ; 正常的输出信号也将变成脉冲信号 , 而且它们的宽度与选通脉冲相同
9.3.3.
指向原始笔记的链接
第五章 半导体存储电路
Transclude of 第五章-半导体存储电路