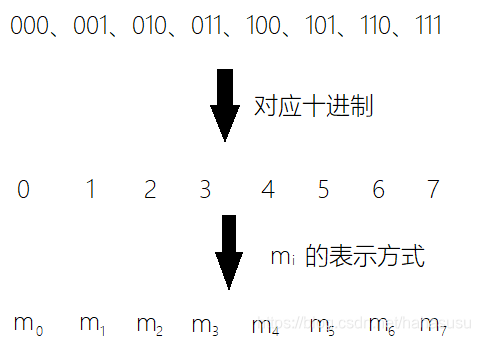
逻辑函数有「最小项之和」和「最大项之积」两种标准形式。首先说明最小项和最大项的概念。
最小项和最大项
最小项
对于
个因子,其最小项 :
是乘积项 - 包含
个因子 个变量均以原变量和反变量的形式在 中出现一次 - 总共有
个
性质
指向原始笔记的链接
- 在输入变量任一取值下,有且仅有一个最小项的值为 1
- 全体最小项之和为 1
- 任何两个最小项之积为 0
- 最小项具有相邻性
- 任何两个最小项如果他们只有一个因子不同,其余因子都相同,则称这两个最小项为相邻最小项。
- 两个相邻的最小项之和可以合并,消去一对因子,只留下公共因子
最大项
在
变量逻辑函数中,若 为 个变量之和,而且这 个变量均以原变量或反变量的形式在 中出现一次,则称 为该组变量的最大项。 性质
指向原始笔记的链接
最小项之和形式
最小项之和
首先将给定的逻辑函数式化为若干乘积项之和的形式(亦称“积之和”形式), 然后再利用基本公式
将每个乘积项中缺少的因子补全, 这样就可以将与或的形式化为最小项之和的标准形式。 转换
最小项之和与最大项之积的关系为
最小项之和可以转化为对应项的最大项之积。
指向原始笔记的链接笔记来源
最大项之积形式
最大项之积
利用逻辑代数的基本公式和原理, 首先我们一定能把任何一个逻辑函数式化成若干项相乘的或与形式(也称“和之积”形式). 然后再利用公式
将每个多项式中缺少的变量补齐, 就可以将函数式的或与形式化成最大项之积的形式了. 指向原始笔记的链接笔记来源