1. 微波集成电路基础
1.1. 电磁理论
第 1 章 电磁理论
[! tldr] 第一章电磁理论的内容是整个微波工程的基石,主要讲解在无耗媒质和有耗媒质以及各种特殊有耗媒质,如良导体、理想导体中对亥姆霍兹方程进行求解。
通过求解亥姆霍兹方程,我们能够求得和波相关的一系列参数,如传播常数、相速度、波长、波阻抗和趋肤深度。
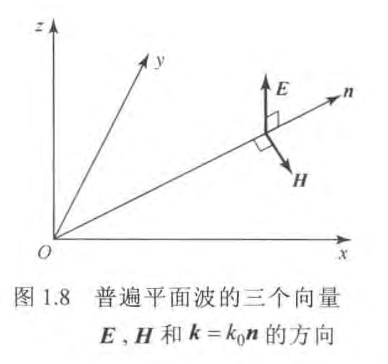
通过对平面波的通解进行求解,我们得以知晓平面波在传播的时候,电场强度方向、磁场强度方向与传播方向的正交性。
麦克斯韦方程组
麦克斯韦方程组
麦克斯韦方程组,是英国物理学家詹姆斯·克拉克·麦克斯韦在 19 世纪建立的一组描述电场、磁场与电荷密度、电流密度之间关系的偏微分方程。它由四个方程组成:
从麦克斯韦方程组,可以推论出电磁波在真空中以光速传播,并进而做出光是电磁波的猜想。麦克斯韦方程组和洛伦兹力方程是经典电磁学的基础方程。从这些基础方程的相关理论,发展出现代的电力科技与电子科技。
Transclude of 有电介质时的麦克斯韦方程组公式微分形式指向原始笔记的链接
算符用于求向量的梯度。 书写体表示时变向量场,它们是空间坐标 x, y, z 和时间变量 t 的实函数。上式均为线性的,但是又是彼此关联的。
电磁场的源是磁流
、电流 和电荷密度 。由于磁流是一个虚拟的源,所以说电荷密度 是电磁场最根本的源。 真空中电场强度、磁场强度与其通量密度之间存在的简单关系
指向原始笔记的链接
为磁通量密度; 为真空磁导率; 为磁场强度; 为电通量密度; 为真空介电常数; 为电场强度。 媒质中的场和边界条件
对于电介质材料,外加电场
使材料的原子或分子产生极化,进而导致电偶极矩,它增大了总的位移通量 。这个附加的极化向量称为电极化强度 , 在线性媒质中,电极化强度与外加电场呈线性关系,
为电极化率,它可能是复数。 介电材料的损耗还可以考虑有一个等效的导体损耗。在电导率为
的材料中,传导电流密度为, 上述讨论中假设
是与 同方向的向量。这种材料称为各向同性材料,但并非所有材料都具有这种特性。有些材料是各向异性的,它们用 和 或 和 之间更复杂的关系来表达。这些向量之间的最一般的线性关系取二阶张量的形式,可以用矩阵形式表示。 类似的情形也出现在磁材料中。
波方程和基本平面波的解
亥姆霍兹方程
在无源、线性、各向同性和均匀的区域,对向量形式的麦克斯韦方程组中的未知量
和 求解,由此得到亥姆霍兹方程。 亥姆霍兹方程即为电场强度的波方程。亥姆霍兹方程公式
指向原始笔记的链接 对于磁场强度,同样有完全相同的波方程。
无耗媒质中的平面波
在无损媒质中,亥姆霍兹方程的参数都是实数,可以将其简化为,
上式可以得到两个独立的解,频率
时谐形式为, 在时域可以写为,
为了保持波的一个固定点相位(即
为常数),当时间增加,其必须移动。由此可推出相速的计算公式, 相位速度计算式
指向原始笔记的链接
为角频率; 为传播常数; 为磁导率; 为介电常数。 波长计算式
指向原始笔记的链接
为传播常数; 为相速度; 为角频率; 为频率。 一般有耗媒质中的平面波
有耗媒质的复传播常数公式
指向原始笔记的链接
为衰减常数; 为相位常数。 良导体中的平面波
良导体是前面分析过的导电电流比位移电流大得多的一种特殊情况,即
。绝大多数金属都可视为良导体。宁可采用复介电常数,也不采用电导率。忽略位移电流项,复传播常数能近似为, 复传播常数在良导体中的近似公式
指向原始笔记的链接
为衰减常数(损耗); 为相位常数(速度) 由此定义了趋肤深度,
趋肤深度计算式
指向原始笔记的链接
为导体的电阻率; 为角频率; 为频率; 为相对磁导率; 为真空磁导率; 为电导率; 平面波的通解
通过使用分离变量法对波动方程进行求解,得到电场振幅向量
和磁场强度向量 , 这说明,
- 电场振幅向量
垂直于传播方向 ; - 磁场强度向量
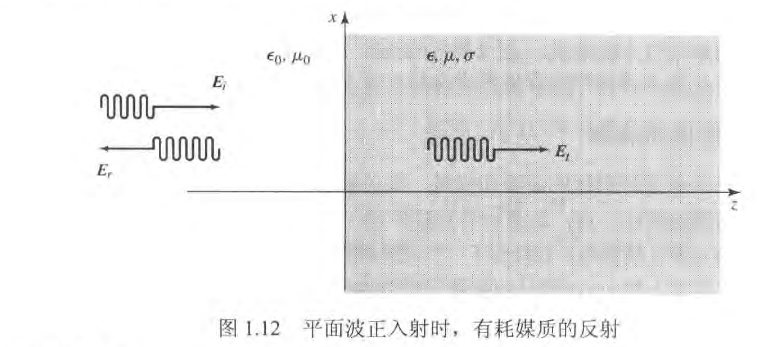
垂直于传播方向 的平面,同时也垂直于 。 媒质分界面上的平面波反射
其中
的有耗半空间由参量 、 和 表征。 普通媒质
通过对入射场、反射场和透射场的电磁分析,我们了解到现在存在着边界值问题,其中场的普遍形式在
处的材料不连续的两边都是已知的。于是就能通过这些场的公式推得未知反射电场的反射系数 和透射电场的透射系数 。 正入射到有耗材料分界面上的波的反射系数通解计算式
指向原始笔记的链接
为材料的阻抗; 为系统特征阻抗 正入射到有耗材料分界面上的波的透射系数通解计算式
指向原始笔记的链接
为反射系数; 为材料的阻抗; 为系统特征阻抗 是材料的阻抗。 无耗媒质
若
的区域是无耗媒质,则有 ,且 和 都是实数。这种情况下的传播常数是纯虚数,因而可以写为, 媒质中的波长为,
相速为,
媒质中的波阻抗为,
指向原始笔记的链接
1.2. 传输线理论
第 2 章传输线理论
[! tldr] 这一章的主要内容是介绍了传输线理论并且将电磁理论运用到对传输线的分析上面。
通过电报方程求解在传输线上传播的波的波方程,然后对波方程进行求解得到波阻抗、相速度、波长。
传输线是由传播常数和特征阻抗来表征的。然后拓展到无损以及高频低耗情况下的上述参数。随后我们考虑了无损传输线端接负载的情况,考虑了端接负载所引起的波反射以及如何计算反射波和损耗以及度量传输线的失配量的参数,即反射系数、回波损耗和SWR。随后学习使用史密斯圆图对电路进行分析和匹配。
传输线的集总元件电路模型
电路理论和传输线理论之间的差别
电路理论和传输线理论之间的关键差别是电尺寸。电路分析假设网络的物理尺度比电波长小得多,而传输线的尺寸可能为几分之一个波长或几个波长。因此,传输线是分布参数网络,在整个长度内其电压和电流的幅值与相位都可能发生变化。
传输线方程
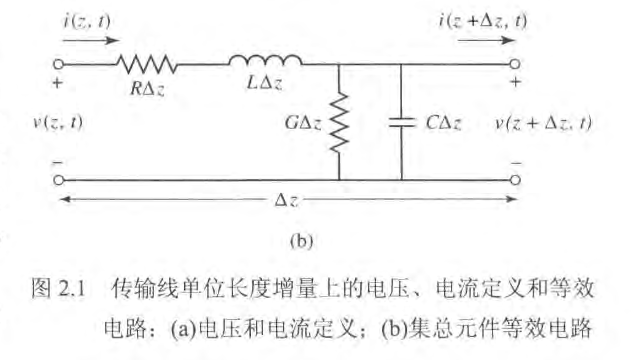
上图是传输线可建模为上图中的集总元件电路,其中的参数都是单位长度的量。
串联电感
代表两个导休的总自感,并联电容 来源于两个导体的紧密贴近。串联电阻 代表两个导体的有限电导率产生的电阻,并联电导 来源于两个导体间填充材料的介电损耗。 通过使用基尔霍夫电压定律和基尔霍夫电流定律进行分析,能得到电报方程的时域形式,
电报方程时域形式
指向原始笔记的链接 传输线上的波传播
通过联立电报方程得以求解关于电压电流的波方程,然后求出其行波解,
通过将特征阻抗
定义为, 传输线特征阻抗定义式
指向原始笔记的链接
为两个传输线导体的有限电导率产生的电阻; 为传输线两条导体总自感; 为传输线两个导体间填充材料的介电损耗; 为传输线两个导体靠近产生的电容。 以此联系传输线上的电压和电流。
根据 波方程和基本平面波的解 这一节的内容,可以推断出传输线中传输的波的相速度和波长。
无损传输线
在实际情况中,传输线的损耗可以忽略,由此传播常数和特征阻抗都可以近似为实数。
同样可以简化特征阻抗、波长和相速。无损传输线的传播常数计算式
其中,
指向原始笔记的链接; 为角频率; 为单位长度电感; 为单位长度电容。 无损传输线的特征阻抗计算式
指向原始笔记的链接
为传输线单位长度电感; 为传输线单位长度电容。 无损传输线的波长计算式
指向原始笔记的链接
是传播常数的虚数部分; 为传输线单位长度电感; 为传输线单位长度电容; 为角频率。 无损传输线的相速计算式
指向原始笔记的链接
为角频率; 为传播常数的虚数部分; 为传输线单位长度的电感; 为传输线单位长度的电容。 端接负载的无耗传输线
上图画出了一个端接任意负载阻抗
的无耗传输线。这个问题将说明传输线中的波反射,这是分布系统的一个基本特性。 假定有一个形式为
的入射波产生于 处的源。我们知道这一行波的电压和电流之比就是特征阻抗 。当入射波 的特征阻抗为 ,传输线端接的任意负载 负载上电压电流之比应该是 。要满足这个条件,必定会产生具有适当振幅的反射波。 传输线上的总电压
指向原始笔记的链接 传输线上的总电流
指向原始笔记的链接 为什么在考虑反射波的时候,电压相加而电流相减?
需要注意平面波的通解的内容。平面波在介质界面反射的时候,电场强度方向不变,而磁场强度方向则会转
,而电压是电场产生的,电流则是磁场产生的。因此会有不一样的变化。 将负载上的总电压和总电流通过负载阻抗联系起来,在
处有, 由此可以求得反射波。入射电压波振幅对反射电压波振幅的归一化,定义为电压反射系数
, 用波的形式表达就是,
Note
这里需要对电压反射系数有个更深入的理解,为什么电压反射系数的范围是
。首先,电压是以波的形式存在,由于能量守恒定律的存在,在考虑波的反射的时候,不会有更多的波产生,于是振幅绝对值的最大值为「1」。其次,为什么会出现负数,负数意味着电压振幅产生了反向。 于是线上的总电压和总电流可以写为,
从这些表达式可以看出,线上的电压和电流是入射波和反射波的叠加:这样的波称为驻波。只有当反射系数为 0 的时候,才不会有反射波。若
,则没有功率到达负载。 当负载失配时,不是所有来自源的可用功率都传给了负载。这种“损耗”称为回波损耗 ( Return Loss, RL) ,它定义 (以 dB 为单位 )为,
负载匹配(回波损耗定义式
指向原始笔记的链接
为回波损耗,单位为 ; 为输入功率; 为反射功率; 为反射系数。 )具有 的回波损耗(无反射功率)。而全反射( )则具有 的回波损耗(所有入射功率均被反射)。 当负载匹配的时候,传输线上的电压幅值
为常数,可被称为平坦的。当负载失配的时候,反射波会导致驻波,由此导致电压幅值不是常数。此时有电压幅值为, 根据相位项
从 变化,传输线上的电压幅值从 变化到 。当 增加时, 与 之比增加,由此来度量传输线的失配量,称为驻波比 (Standing Wave Radio, SWR) ,可以定义为, SWR 定义式
指向原始笔记的链接
为反射系数。 ,而最大值和相邻最小值之间的距离是 ,其中 是传输线上的波长。 电压的振幅是随着线上的位置而起伏的,由此可以知道,线上的阻抗也必定随位置变化。在距离负载
处,向负载看去的输入阻抗是, 传输线阻抗方程
指向原始笔记的链接
为输入阻抗; 为反射系数; Smith 圆图
史密斯圆图提供了一种使传输线现象可视化的方法,学会如何用史密斯图来思考问题,就能直观地求解传输线和阻抗匹配问题。
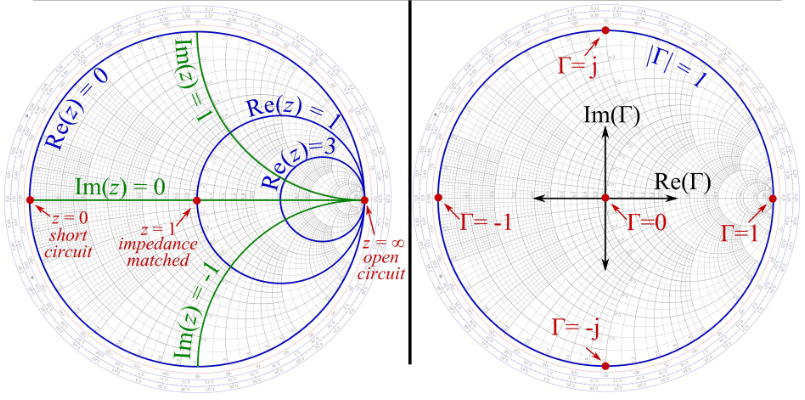
史密斯圆图
史密斯圆图是一个用于辅助设计的工具。
史密斯圆图的构成
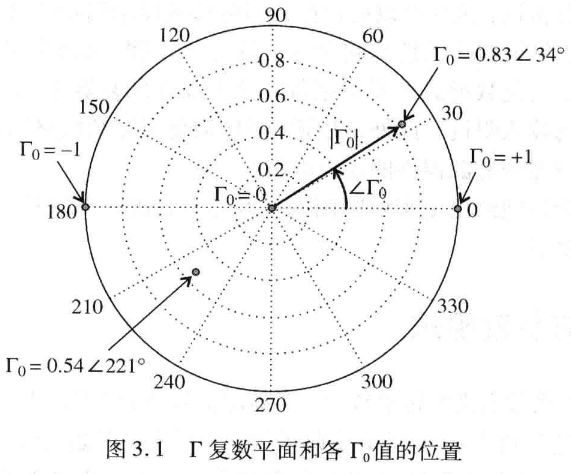
史密斯圆图基本上就是一个电压反射系数
的极坐标图。 首先,把反射系数用幅值和相位(极角) 的形式表示为
。然后把幅值 画成从图中心算起的半径( ) ,把角度 ( )画成是从水平直径的右手边算起的角度。任何无源的可实现的( )反射系数都可以在 Smith 圆图上画成一个唯一的点。 归一化阻抗点
史密斯圆图的真正有用之处是画在图中的阻抗(或导纳)圆,阻抗(或导纳)圆可用来将反射系数转换为归一化阻抗(或导纳),反之亦然。处理图中的阻抗的时,通常用归一化的量。
归一化阻抗计算式
指向原始笔记的链接
为线路的负载阻抗; 为传输线的特征阻抗; 为传输线电阻; 为传输线电抗 根据归一化阻抗即可在史密斯圆图上找到对应的点。归一化阻抗的实数部分对应电阻圆,虚数部分对应电抗圆。
归一化阻抗点与圆心的距离,对应到史密斯圆图的水平标尺
TRANSM.COEFF,E or I即可找到对应的值(注意起始点的位置)。 也可以根据以下变换公式, 将归一化阻抗转换为复反射系数
映射到史密斯图上: 归一化阻抗导纳到反射系数的变换公式
指向原始笔记的链接
为归一化阻抗; 为归一化导纳 计算出的
即为对应的坐标,通常用极坐标表示。
通过这个转换, 可以将复阻抗
平面上的每一个点, 映射到史密斯图的 平面上。这实际上建立了两个复平面之间的一对一映射关系。这就是史密斯图的定义。它实现了从复阻抗平面到复反射系数环形坐标系的转换, 并建立了二者之间的映射对应关系, 以此来分析和设计微波电路中的匹配网络。
史密斯圆图的应用
史密斯圆图的应用
基本运用
求解负载处的反射系数、传输线输入端的反射系数、输入阻抗、传输线的 SWR 及回波损耗
一个
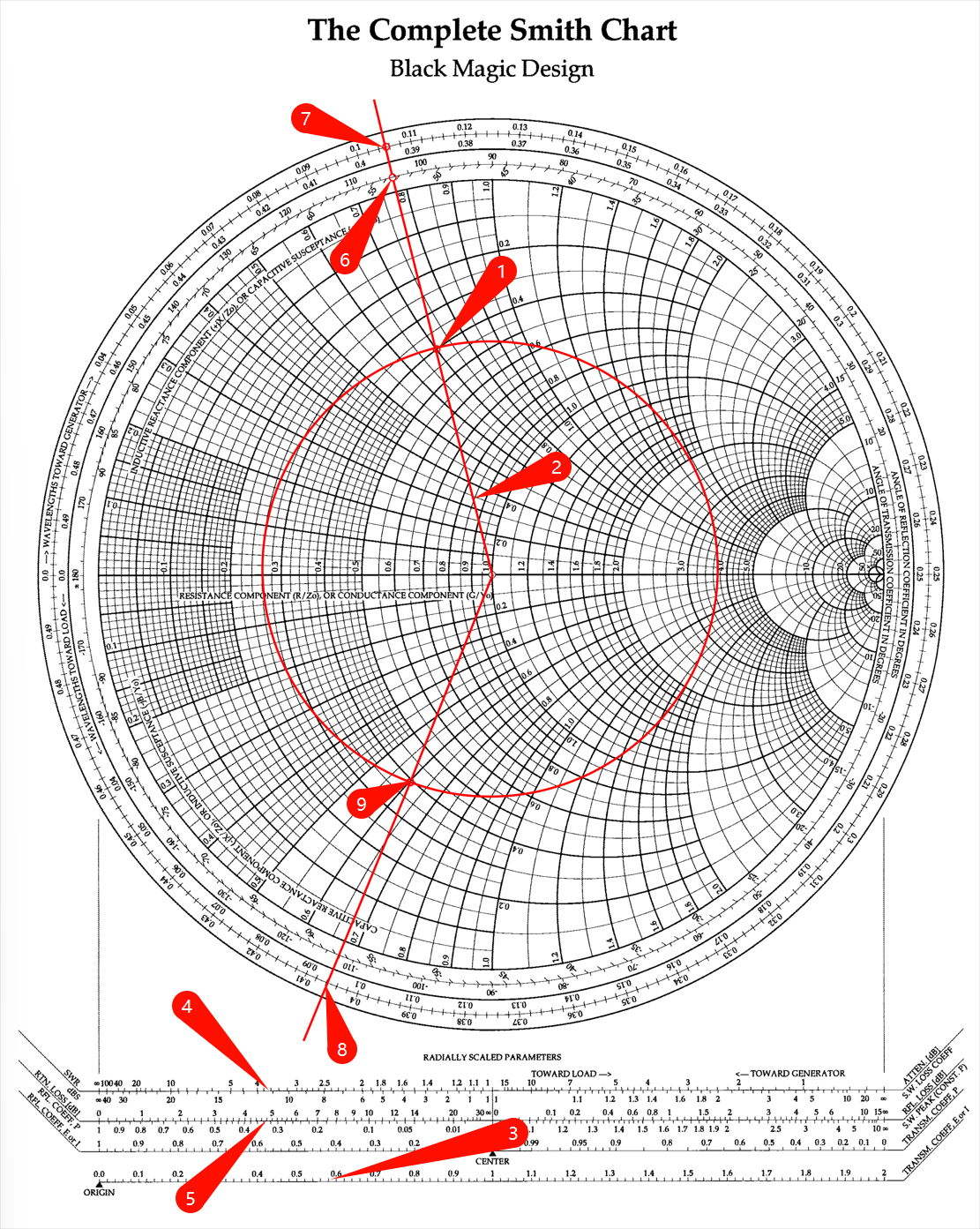
的负载阻抗接在一条 的传输线上,其长度为 求负载处的反射系数、传输线输入端的反射系数、输入阻抗、传输线的 SWR 及回波损耗。
首先计算归一化负载阻抗,
为图中1️点。利用圆规及圆图下面的电压反射系数标尺,可以读出负载处的反射系数幅值
TRANSM.COEFF, E or I(3),驻波比SWR(4),回波损耗标尺RTN.LOSS[dB](5)。[! note] 在画出等 SWR 圆之后,也可在阻抗匹配点右侧 x 轴与圆的交点出读出 SWR 值。
现在,通过阻抗负载点画一条径向线(2),然后从它与图的外围标尺上的交点读出负载处反射系数的辐角(6)。
现在通过负载阻抗点画一个 SWR 圆。读出负载在朝向波源波长 (WTG) 标尺上的参考位置的值为
(7)。向着波源方向移动 把我们带到 WTG 标尺上的 处(8)。在此位置画一条径向线,它与 SWR 圆的交点给出归一化输入阻抗的值 (9)。于是传输线的输入阻抗为, RC 网络阻抗匹配
阻抗计算
电容阻抗计算式
指向原始笔记的链接 电感阻抗计算式
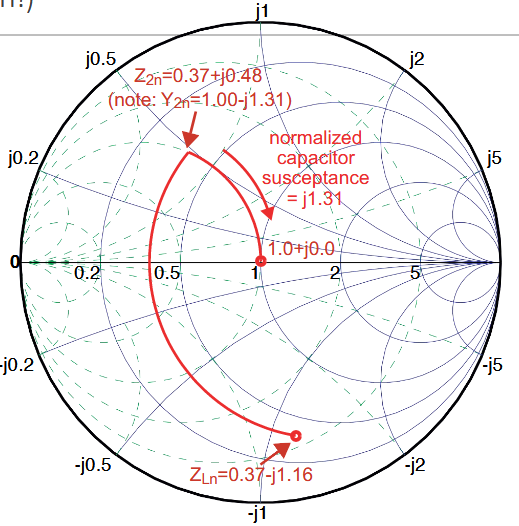
指向原始笔记的链接 计算出负载阻抗之后,将其归一化并标注在史密斯圆图上。
规划移动路线并计算对应的电容电感值
通过串并联电容电感我们能够使得圆图上的点沿着电阻圆或者电导圆顺时针或逆时针移动。通常我们首先将其移动到
或 等于 1 的圆上,然后再移动到匹配点。
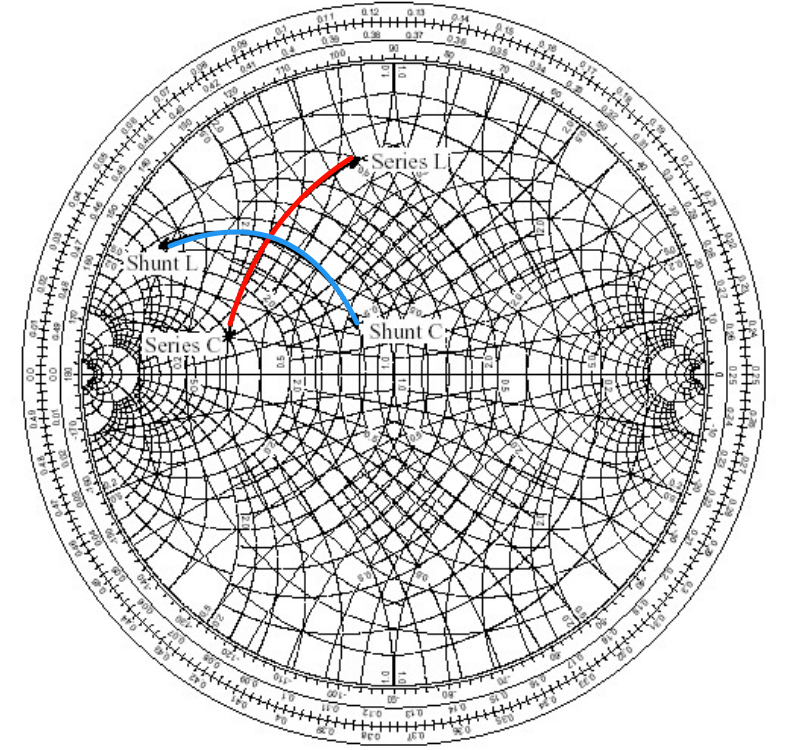
[! tip] 使用 RC 网络进行匹配的时候有以下规律
- 串联电感:正电抗将导致负载沿着等电阻圆顺时针移动;
- 串联电容:负电抗将导致负载沿着等电阻圆逆时针移动;
- 并联电感:负电纳将导致负载沿着等电导圆逆时针移动;
- 并联电容:正电纳将导致负载沿着等电导圆顺时针移动。
简而言之,
- 串联顺着电阻圆移动,并联顺着电导圆移动
- 使用电感就是 Levitate(抬升),使用电容就是Crush(下降)
根据规划的路线进行计算
电容阻抗计算式
指向原始笔记的链接 电感阻抗计算式
指向原始笔记的链接 组合阻抗-导纳的 Smith 圆图
因为绕 Smith 圆图一剧对应于
的长度,所以 的变换等价于在圆图上旋转 ;这也等价于镜像个给定的阻抗(或导纳点)穿过圆图的中心就得到对应的导纳(或阻抗)点。 史密斯圆图含意
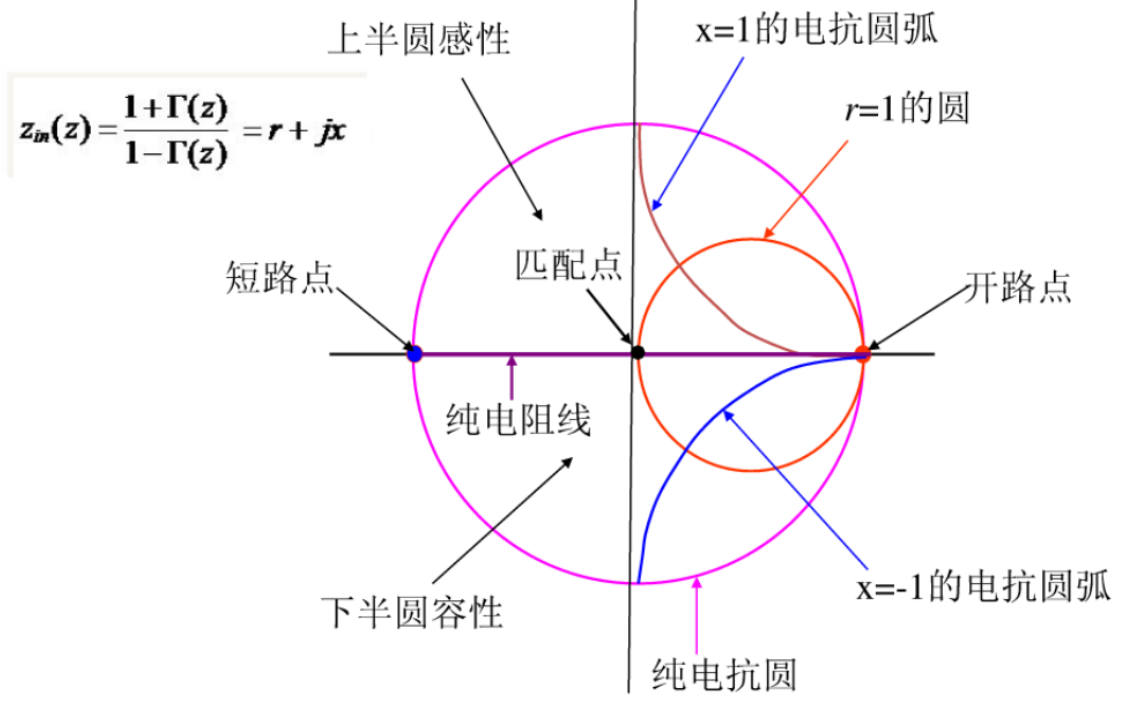
根据上面的推导,可以得出下面的简化圆。
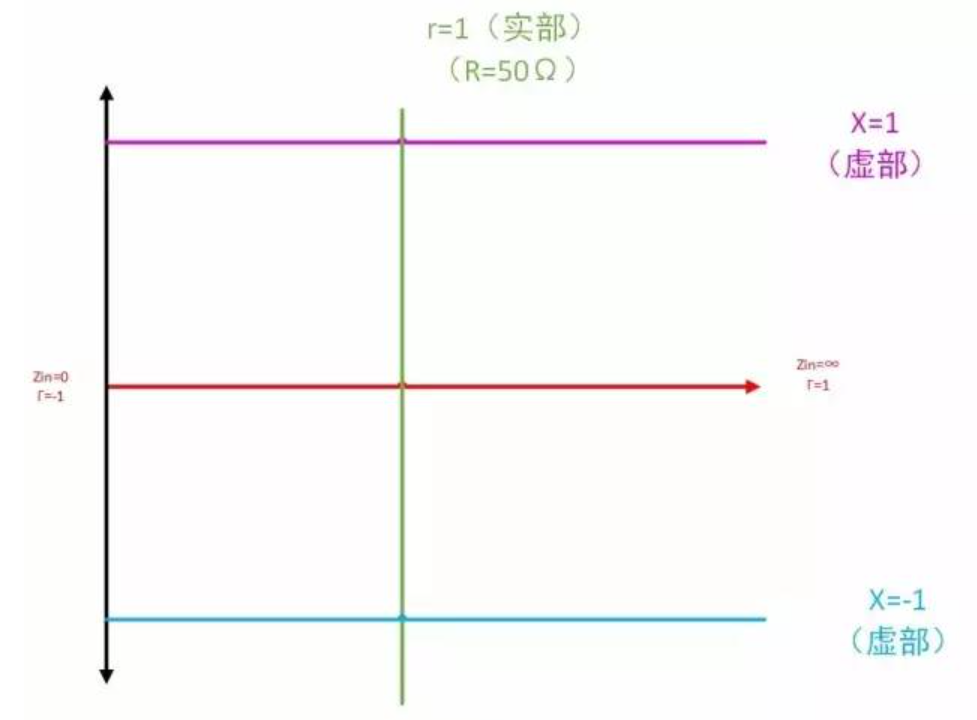
史密斯圆图在作图时,有五条定义线。我们以电阻圆为基础进行讲解。
- 电阻为 0 的黑色线
- 电抗为 0 的红色线
- 电阻为 50
的绿色线 - 电抗为 1 的紫色线
- 电抗为 -1 的蓝色线
画成史密斯圆图的样子如下。
将部分参数标注出来如下。
参考信息
指向原始笔记的链接Info
源和负载失配
共轭匹配
对于固定的源阻抗
,当输入电阻等于源电阻,输入电抗等于负源电抗, 即,
满足这个条件的输入阻抗可以使得最大功率传到负载。此时功率为,
有耗传输线
低耗线
如果传输线是低耗的,可以假定
和 ,这意味着导体损耗和电介质损耗都很小,此时有 ,复传播常数表达式可以简化为, 传输线复传播常数高频低耗近似
指向原始笔记的链接 传输线传播常数α高频低耗近似
指向原始笔记的链接 传播常数β高频低耗近似
指向原始笔记的链接 采用同级近似,特征阻抗
可以近似为实数量, 传输线特征阻抗高频低耗近似
指向原始笔记的链接
1.3. 微波网络分析
第 4 章 微波网络分析
Tldr
本章的意图是说明如何推广电路和网络概念,以便处理很多微波分析和设计问题。用电路的概念分析微波问题更加简单和直观。
微波网络分析的基本过程
- 首先用场分析和麦克斯韦方程组严格地处理一批基础性的标准问题 (如在第 2 章和第 3 章中所做的那样,处理各种各样的传输线和波导问题)。
- 得出一些量,并且它们可与电路或传输线参量直接建立联系(如传输线的传播常数和特征阻抗)。把传输线或波导处理成可用长度、传播常数和特征阻抗表征的分布元件。
- 把不同元件互连起来,并用电路和/或传输线理论来分析整个元件系统的性能,如多次反射、损耗、阻抗变换及从一种到另一种传输媒质 (如从同轴线到微带 )的过渡
阻抗和等效电压与电流
等效电压和电流
在微波频率下,电压和电流的测量非常困难 (或不可能 ),除非能够得到明显确定的一对端点。
TEM 型传输线 (如同轴线、微带线或带状线)存在这样的一对端点,而非 TEM 型传输线 (如矩形、圆形或表面波波导) 严格来说不存在这样的一对端点。
对于任意截面形状双导线 TEM 传输线的电力线和磁力线。正导线相对于负导线的电压可求出如下,
式中,积分路径始于+导线,终于 -导线。注意,由于两根导线之间的横场具有静态电场的性质,因此式中定义的电压是唯一的,它与积分路径的形状无关。
应用安培定律,正导线中的总电流为,
式中的积分回路是围绕+ 导线 (但不包括 -导线 ) 的任意封闭路径。
因此,行波的特征阻抗
定义如下, 阻抗概念
阻抗一开始被用于描述交流电路中的复数比
;随后被应用到集总元件等效电路以及分布式串联阻抗和并联导纳表示的传输线上;之后又被推广到了电磁场,看成场的特征之一,其还与方向有关。 媒质的本征阻抗
媒质的本征阻抗
媒质的本征阻抗仅与媒质的材料参量有关,并且等于平面波的波阻抗
指向原始笔记的链接媒质的本征阻抗计算式
指向原始笔记的链接
为磁导率; 为介电常数。 波阻抗
波阻抗
这个阻抗是特定波的一种特性。TEM 波、TM 波和 TE 波有着不同的波阻抗 (
, , ),具体取决于传输线和波导的类型、材料性质及工作频率。 波阻抗计算式
指向原始笔记的链接 特征阻抗
特征阻抗
特征阻抗决定了行波电压与电流在传输线中的比例。因为 TEM 波的电压和电流是唯一确定的,所以 TEM 波的特征阻抗也是唯一的。然而,TE 波和 TM 波并不存在唯一确定的电压和电流,因此这些波的特征阻抗可用不同的方式来定义。
指向原始笔记的链接特征阻抗定义式
指向原始笔记的链接
为入射电压; 为反射电压。 阻抗和导纳矩阵
在等效电压和电流那一节,我们已经能够确定整个网络中不同点的电压和电流,然后就能用电路理论的阻抗和导纳矩阵把这些端点量或“端口”量联系起来,进而使用矩阵对网络进行描述。
类似地有,
很明显有
。 由上面关于
的矩阵可以知道, 为, 换言之,上式说明
可以通过激励电流为 的端口 , 而其他所有端口开路 (故有 , ) 并测量端口 的开路电压得出。 散射矩阵
在测量高频网络的时候,电压和电流往往难以直接测量,因为直接测量通常会涉及给定方向的行波或驻波的幅值 (得出功率 ) 与相位。
类似与阻抗和导纳矩阵将端口上的电压和电流联系起来了,散射矩阵将入射到端口的电压波和来自端口的反射波联系了起来,由此散射矩阵提供了从端口看去的完整网络描述。
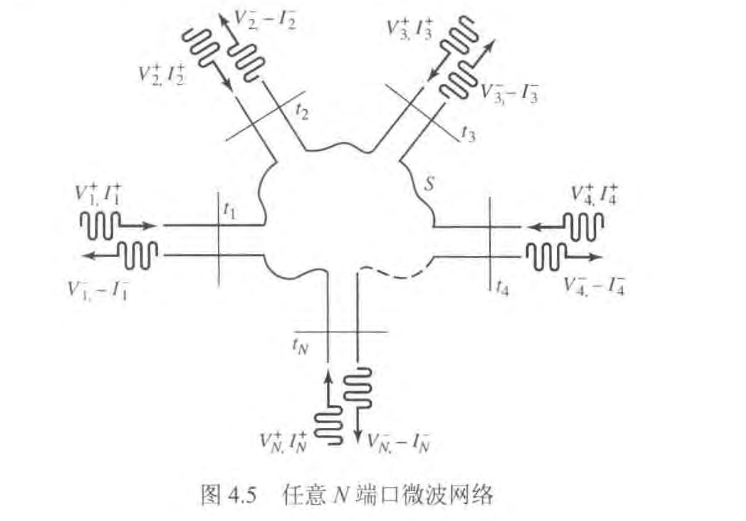
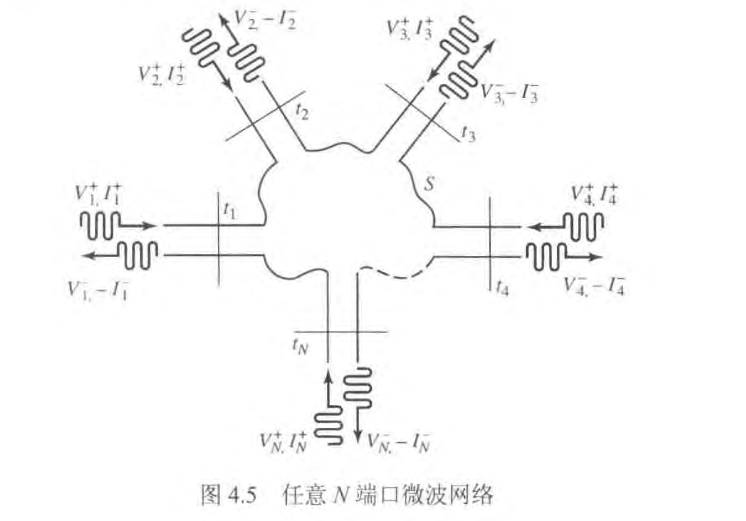
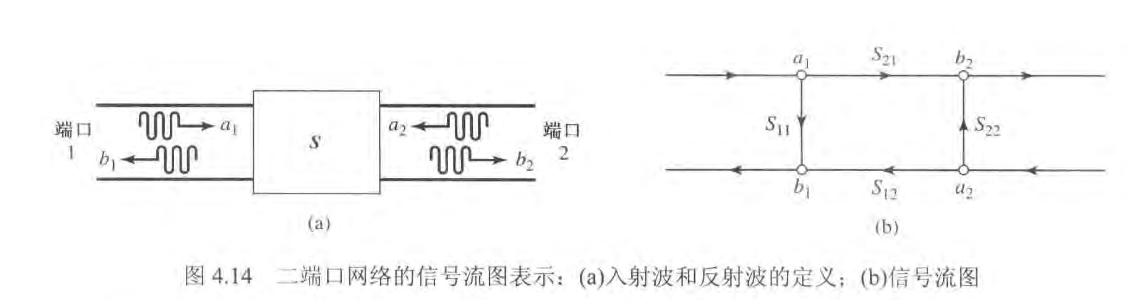
考虑上图的 N 端口网络,其中
是入射到端口 的电压波振幅, 是从端口 反射的电压波振幅。
矩阵的元素为, 换言之,上式说明,使用入射波电压
激励 端口并测量从 端口出来的反射波电压 ,可得出 。同时要求将除 端口外的所有其他端口上的入射波设为零,这意味着所有端口应端接匹配负载以避免出现反射。这样, 就是所有端口接匹配负载时向 端口看去的反射系数(向端口 看去的反射系数并不等于 ,只有当所有的其他端口都匹配时才会这样),而 是所有其他端口接匹配负载时从 端口到 端口的传输系数。 互易网络与无耗网络
如果网络是互易的,那么有,
即
参数是对称的。 如果网络是无耗的,那么有
可以取
进行测试,即计算 是否等于 1。 功率波和广义散射参量
整理传输线上的总电压和传输线上的总电流这两个公式,可以得到入射电压和反射电压波振幅,
传输线入射电压波振幅
指向原始笔记的链接 传输线反射电压波振幅
指向原始笔记的链接 定义一种称为功率波的新波来处理信号源和负载之间的功率传输问题,且其同时适用于无耗和有耗传输线。
入射和反射功率波振幅
和 可定义为电压和电流的如下线性变换: 传输线入射功率波振幅
指向原始笔记的链接
为参考阻抗。 传输线反射功率波振幅
指向原始笔记的链接
为参考阻抗。 负载处反射功率波反射系数
指向原始笔记的链接 信号流图
信号流图的基本组成
信号流图的基本组成是节点和支路:
指向原始笔记的链接
- 节点:微波网络的每个端口
有两个节点 和 。节点 等同于进入端口 的波,而节点 等同于自端口 反射的波。节点的电压等于所有进入该节点的信号之和。 - 支路:支路是两个节点之间的有向路径,代表信号从一个节点向另一个节点流动。每条支路都有相关联的
参量或反射系数。
1.4. 阻抗匹配
第 5 章 阻抗匹配和调谐
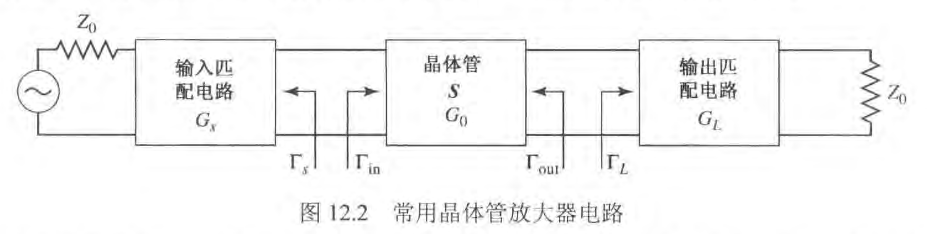
阻抗匹配的基本思想如上图所示,它将阻抗匹配网络放在负载和传输线之间。为了避免不必要的功率损耗,理想的匹配网络是无耗的,并且通常设计成向匹配网络看去的阻抗是
。虽然在匹配的网络和负载之间存在多次反射,但在匹配网络的左侧消除了传输线上的反射。这个过程也称调谐。 用集总元件匹配(L 网络)
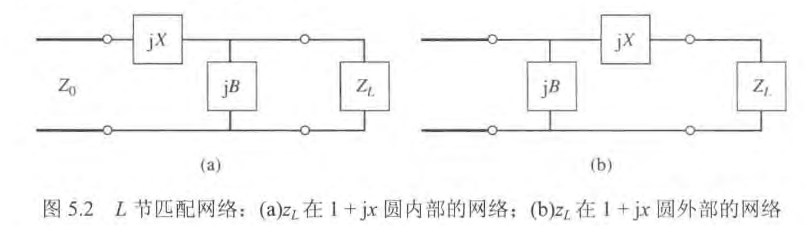
这种
节有两种可能的结构,如下图所示。归一化负载阻抗 在 Smith 圆图的 圆的内部时,应使用图 5.2a 所示的电路。归一化负载阻抗 在 Smith 圆图的 圆的外部时,应使用图 5.2b 所示的电路。 圆是在 Smith 阻抗圆图上 的电阻圆(过匹配点的圆)。 史密斯圆图解法
Hint
这里有几个要点需要注意,
- 通常我们选择移动的最短距离来规划路线,但是两种移动方式都是可行的;
- 在史密斯图上计算都是归一化的值,在匹配时需要还原为原始值;
- 首先需要确定使用哪种
网络。 RC 网络阻抗匹配
阻抗计算
电容阻抗计算式
指向原始笔记的链接 电感阻抗计算式
指向原始笔记的链接 计算出负载阻抗之后,将其归一化并标注在史密斯圆图上。
规划移动路线并计算对应的电容电感值
通过串并联电容电感我们能够使得圆图上的点沿着电阻圆或者电导圆顺时针或逆时针移动。通常我们首先将其移动到
或 等于 1 的圆上,然后再移动到匹配点。
[! tip] 使用 RC 网络进行匹配的时候有以下规律
- 串联电感:正电抗将导致负载沿着等电阻圆顺时针移动;
- 串联电容:负电抗将导致负载沿着等电阻圆逆时针移动;
- 并联电感:负电纳将导致负载沿着等电导圆逆时针移动;
- 并联电容:正电纳将导致负载沿着等电导圆顺时针移动。
简而言之,
- 串联顺着电阻圆移动,并联顺着电导圆移动
- 使用电感就是 Levitate(抬升),使用电容就是Crush(下降)
根据规划的路线进行计算
电容阻抗计算式
指向原始笔记的链接 电感阻抗计算式
指向原始笔记的链接 单短截线调谐
指向原始笔记的链接单短截线调谐
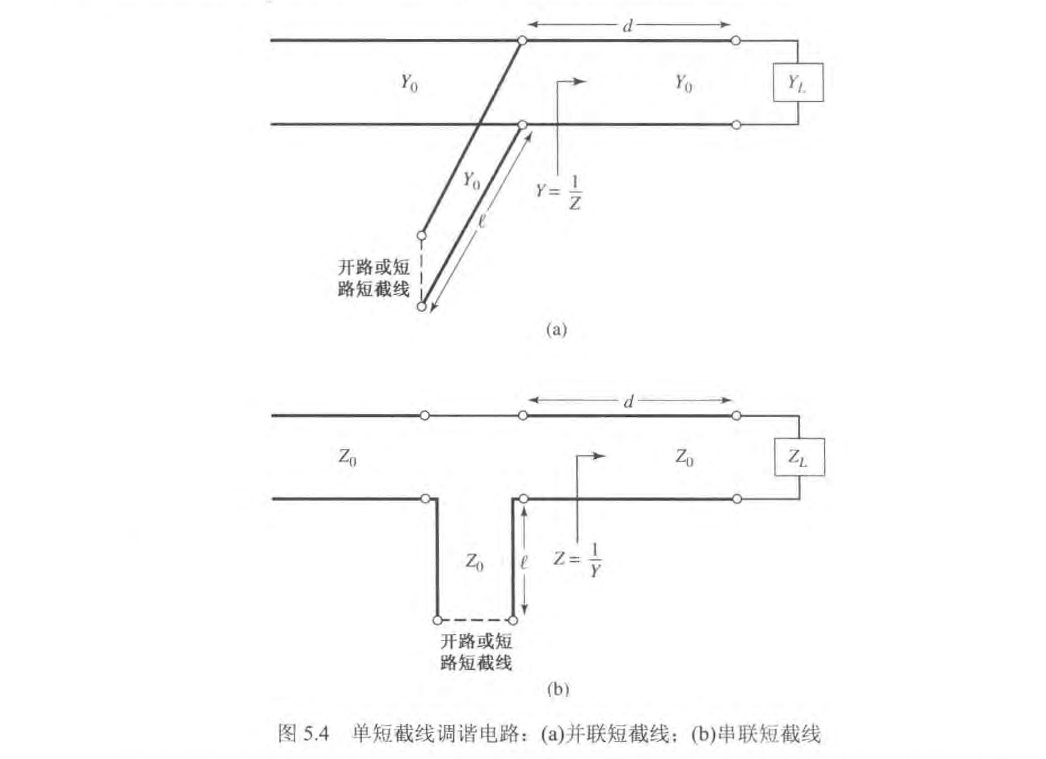
单短截线调谐通过使用单个开路或短路的传输线段(短截线 )在离负载某一确定的位置与传输馈线并联或串联来进行匹配。
调谐方法
在单短截线调谐中,有两个可调参量:从负载到短截线所在位置的距离
和由并联或串联短截线提供的电纳或电抗。 对于并联短截线,基本思想是选择
使其在距离负载 的位置向传输线看去的导纳 具有形式 , 然后将该短截线的电纳选择为 就达到了匹配条件。 对于串联短截线,选择距离
使其在距离负载 的位置向传输线看去的阻抗 具有形式 , 然后将该短截线的电抗选为 就达到了匹配条件。 并联短截线
用史密斯图进行求解
指向原始笔记的链接
- 在史密斯图上标出归一化负载阻抗点,并画出对应的 SWR 圆;
- 转换到负载导纳
,把史密斯圆图考虑成导纳圆图; - 标出 SWR 圆和
圆的两个交点,并通过 WTG 标尺读出负载到短截线的距离,并选取最近的一个; - 读出选择的交点的归一化导纳值,得出短截线需要的电纳值;
- 计算短路短截线的长度,以
(短路点 )为起点,沿圆图外缘 向信号源方向旋转到对应的电纳点,即可得到对应的长度。
2. 微波半导体材料
2.1. 半导体中的能级结构
一些重要半导体的能带结构
我们在几个板块中绘制 E-k 图,其中 k 沿(100)方向或(111)方向从零到最大值,等等,都在布里渊区内。如图 2.6 中的 fcc 晶格所示,沿 (100) 方向的最大 k 值为 2π/a (1,0,0)。这一点称为 X 点,由于晶格的立方对称性,还有其他五个等效点。同样,沿着 (111) 方向,最大 k 点为 π/a (1, 1, 1) 和其他七个类似点。这个点被称为 L 点。因此,我们通常用 k 从原点(称为 Γ 点)到 X 点以及从原点到 L 点来表示 E-k 图。
直接半导体和间接半导体
能带结构的类型
能带结构有两种类型,直接带隙和间接带隙。
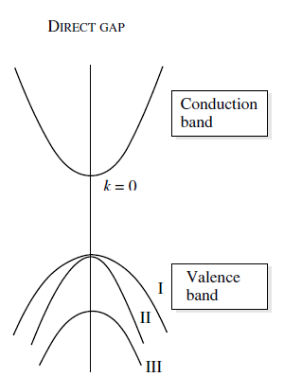
直接带隙
直接带隙指的是价带顶和导带底同时出现在零有效动量处(
)。价带边缘附近有三个带。这些曲线或带在图中分别标为 I、II 和 III,称为重空穴带 (Heavy Hole Band,HH)、轻空穴带 (Light Hole Band,LH) 和空穴分裂带(Split-Off Band,SO)。
当带边处于 k = 0 时,可以用以下简单关系来表示带状结构,
指向原始笔记的链接导带底 E-k 关系
指向原始笔记的链接
为导带底能量; 为约化普朗克常数; 为; 为有效质量。 间接带隙
间接带隙指的是导带底并没有出现在零有效动量处,但是通常来说,大多数的半导体的价带顶都会出现在零有效动量处。
指向原始笔记的链接
直接带隙半导体
当半导体具有直接带隙时,其被称为直接带隙半导体。GaAs、InP、GaN、InN等半导体都属于直接带隙半导体。
指向原始笔记的链接硅
硅是最重要的半导体,它具有间接带隙结构。
由于导带边的六重退化(six-fold degeneracy),硅中的电子传输相当差,因为带边附近的态密度非常大,导致传输中的散射率很高。
GaAs
GaAs 能带结构
砷化镓是一种直接间隙材料,电子有效质量较小。其能带结构如图,
用非抛物线近似能更好地表达这个关系,GaAs能带结构表达式
指向原始笔记的链接
为约化普朗克常数; 为波数; GaAs能带结构非抛物线近似表达式
指向原始笔记的链接
指向原始笔记的链接
谷的有效质量远大于 谷。对于砷化镓, 。这种质量差异对于高电场传输极为重要。 InN, GaN, and AlN
这些材料通常生长为晶圆结构,带隙范围从 1.0 eV 到 6.0 eV 以上。这种大带隙对短波长光发射器和大功率电子器件非常有用。
值得注意的是,半导体的带隙通常会随着温度的升高而减小。
指向原始笔记的链接
2.2. 流动载流子
流动载流子
在金属中,电流的产生是由于存在于最高(部分)填充带中的电子。这些电子的密度非常高(∼ 1023 cm-3)。相反,在半导体中,如果价带充满电子,而导带没有电子,则不会有电流流动。但是,如果通过移除电子在价带中产生某种空态或空穴,电流就会通过空穴流动。同样,如果在导带中加入电子,这些电子也可以携带电流。如图 2.16b 所示。如果导带中的电子密度为 n,价带中的空穴密度为 p,则总的移动载流子密度为 n + p。
金属中的流动电子
在金属中,有一系列填充带和部分填充带,称为传导带。就金属的电学和光学特性而言,填充带是惰性的。金属的传导带可以假定为抛物线能量-动量关系来描述
请注意,我们使用的有效质量等于自由电子的质量。这对金属来说是一个合理的近似值。带内较大的电子密度“屏蔽”了背景电势,电子的有效质量非常接近自由空间值。金属导带抛物线 E-k 关系
指向原始笔记的链接
是导带底能量; 是约化普朗克常量; 是电子波数; 是自由电子质量。 金属导带中的电子密度与费米级的关系式,
这个积分在 0 K 时特别容易求得,因为在这个温度下,金属导带电子密度与费米级的关系式
指向原始笔记的链接 0K 时金属导带电子密度与费米级的关系式
指向原始笔记的链接
是费米能级; 是导带底能量; 是约化普朗克常量; 是自由电子质量; 是电子密度 该表达式适用于铜、金等金属。表 2.2 列出了几种金属的导带电子密度。EF 是 0 K 时的最高能态,称为费米能级。我们可以定义一个相应的波矢,
以及费米速度,费米矢量计算式
指向原始笔记的链接
是电子密度,表示单位体积内的电子数。 费米速度计算式
指向原始笔记的链接
为约化普朗克常数; 为电子有效质量; 是电子密度,表示单位体积内的电子数; 为费米波矢。 ,而不是使用经典统计法情况下的 0。在有限温度下,费米级的近似值为, 有限温度下费米能级的近似值
其中
指向原始笔记的链接和 分别是温度为 TK 和 0K 时的费米能级;
2.3. 微波半导体材料的选择
Transclude of Chapter-11-Microwave-semiconductor-materials-and-diodes#微波半导体材料的选择
2.4. 半导体材料制造
微波半导体制造技术
有源电子器件通常是在基底上生长的外延层中制造的。低电阻率和高电阻率基底均可使用,具体取决于要制造的器件类型。
- 低电阻率基底通常用于垂直器件,如二极管和双极晶体管,在这些器件中,电流必须垂直通过基底材料。
- 高电阻率基底用于面向表面的器件,如场效应晶体管,在这种器件中,电流平行于基底。对于后一种器件,要实现良好的直流和射频性能,通常需要将电流限制在外延层内,并阻隔基底。
光刻
- 清洁和准备。用溶剂去除所有有机污染物,然后加热烘干。随后涂上「附着力促进剂」以增加光刻胶和晶圆之间的附着力,随后烘干;
- 涂上光刻胶。涂上光刻胶,随后加热去除溶剂;
- 光刻胶曝光。预烘烤后,光阻通过掩模暴露在强光下,掩模定义了表面所需的电路图案;
- 光刻显影。使用显影剂去除被曝光区域,随后再烘烤固化光刻胶;
- 蚀刻。在没有光刻胶保护的区域使用化学蚀刻剂去除基底的最上层,通常使用干法蚀刻以制成各向异性的图案;
- 光刻胶去除。使用光刻胶剥离剂剥离光刻胶。
分子束外延
分子束外延(Molecular Beam Epitaxy,简称MBE)是一种精密的工艺过程,涉及将不同半导体元素的分子束发射到样品上,以堆积不同材料的薄层。通常情况下,每种元素都通过单独控制的束流进行输送,因此可以为任何给定层调整元素的选择及其相对浓度,从而定义该层的精确组成以及电学和光学特性。
指向原始笔记的链接
2.5. 材料在微波频率下的特性
微波频率的材料特性
材料的许多特性在较高频率下会发生显著的变化。趋肤效应是决定微波频率下导线有效电阻的一个主要因素。介电常数和磁导率是电容和电感的主要决定因素,两者也与频率有关。
电阻
电阻率的倒数是电导率,
电阻率公式
指向原始笔记的链接
为电导率; 为电阻; 为材料横截面积; 为材料长度。 电导率公式
指向原始笔记的链接
是电子电荷; 是电子浓度; 是电子的迁移率。 电阻计算式
指向原始笔记的链接
为电阻率; 为线长度; 为横截面积 趋肤效应
趋肤效应
在直流时,电流在导体内均匀流动。在较高频率下,电流倾向于沿导体表面聚集。这种行为称为趋肤效应。
由于趋肤效应,电流流过的横截面积大大减小,从而导致了导体的交流电阻远高于直流电阻。对于交流信号,电压和电流正弦波也可能彼此异相,这表明电路中存在电容或电感。
趋肤深度计算式
指向原始笔记的链接
为导体的电阻率; 为角频率; 为频率; 为相对磁导率; 为真空磁导率; 为电导率; 电压和电流发生了异相为什么表明电路中存在电容或者电感?
因为电容或者电感都是储能器件,在电流发生变化的时候,电压会先(电容)后(电感)达到峰值。
趋肤效应电流密度计算公式
指向原始笔记的链接
为导体表面的电流密度; 为距离表面的深度; 为趋肤深度。 趋肤效应电阻计算式
指向原始笔记的链接
为导体长度; 为电阻率; 为导体直径; 为趋肤深度。 介电常数和磁导率
磁导率
磁导率是一个物理常数,定义了材料对磁场的响应程度。
指向原始笔记的链接磁导率定义式
指向原始笔记的链接
是磁通密度的大小; 是磁场强度的大小。 大多数材料的磁导率非常接近真空。不过,含铁、铬或镍的材料相对磁导率(
)更高。 有些材料会表现出与外加磁场方向相反的感应磁场。这些材料被称为二磁材料。二磁材料会被外加磁场排斥。其他一些材料会被外加磁场吸引,并在外加磁场的方向上形成内部感应磁场。这些材料被称为顺磁性材料。铁磁性材料是指在没有外加磁场的情况下仍能保持磁化的材料。永磁体就是由这些材料制成的。磁导率是决定表皮深度的重要因素,因为相对磁导率越高,电磁波穿透材料的程度就越低。
介电常数是指材料对外部施加的电场产生极化反应,从而降低材料内部总电场的能力。换句话说,介电常数是衡量材料内部传递(或 “允许”)电场的能力。与磁导率一样,介电常数通常取决于外加电场的频率。这种频率依赖性反映了这样一个事实,即材料的极化不会即时响应外加磁场。外加磁场与响应之间存在一定的延迟,可以用给定频率下的相位差来表示。
微波频率下电介质和磁性材料的损耗
当对材料施加时变电场时,材料内部的极化偶极子会随着电场来回翻转。电荷载流子的有限质量会产生两个重要后果。首先,移动电荷载流子需要做功,这意味着部分外加能量将 “损失 “在材料中。其次,这些偶极子的移动需要有限的时间,这意味着极化矢量将落后于外加电场。
类似的论点也适用于磁性材料,由于材料内部的磁偶极子对外加磁场的变化做出反应需要能量和时间,因此也会产生损耗和延迟。
当施加外部交变电场或磁场时,材料吸收的功率随频率、磁导率、损耗角正切和外加磁场(电场或磁场)大小的平方呈线性变化。
指向原始笔记的链接
3. 微波晶体管
3.1. BJT
Chapter 6 Bipolar Junction Transistors
%8b8f260bb86b057ad6057ea2290200005ce60515c977243dfacdbb911bcbcf7ajRA0fk8F0vv5lSXnUYLghyI+ZqQkjcGy1gpgZ9T/FwWQLLeHLHiB8TZOz9RGgICWgI3166Ox543B1abGJ4ByTQtWO9X//3pjsX4pyfCbhasyWVuebJZx4qdhGFX4Sr0j6rML+ZQ5Z5v0DL/Ektqu/hmwbEzZHUsaIkY+lyQ/+WnMDdpg2czfOQE7yCAhUXlCjTkoFncKNxmdN8VfMEORKcCLdPkxRLmHwXGtXN/63a8QQQY7k0ZjuyfJNW/uJoTpcfYmk5NFDHibgNcQ+AVj0YGnGm3EghMWs//Wu3jJp7cHn5WCh/HBu2uuvxN343z+bMd2emecM2MctYAJezHRvoHTTA3QT0sOr+oE3aAmecy0QV3Gd8e64gfzru2Z0riqz1/eIL3ZmK3vixOMMPd+MRa2pz4b+9ANfzLR+UjGGFFih9wA2y7QK/4n7RrCWOPCsVvE9eegEKmF+pe2iykGt7dWF8P96qY5DKOMdqKbKjwU7aR8V4CKAEi+Wi8jRqj94qaFEhUsxsKEnKXzz7iwhfPwi/MG+k63zoewyH/rpZHShSYTZrjyMMi4ckLwW6NV26ogHM/5yFxS+pAdvg1f61xqNQcG+/acBC/D9NppaBB8rhXqlyfA0G9KLUEkxPIStgqM8+N1tHnkxfQ8/hsSBesK2mMWMChxzT5ID7cHDMJ+pDLl4IAnKg59fRPZPv+gE/nFWdkkdjNsp4COx/Mc/PrLuBy9GE7ZQgRABc417HE1/mPyk0f6PqxLQ75tAyEdBSL4olSiVfobjOFc1rSLSU7VT2QxII445XzOi72oN3WRWIHrKbCgTeMKZJIVORkTbUcI9oqhvT+8doTCiSncBqWbETvqHz/MjDN7rYUVvsh0KkJyLDD3+UWm0TjiHAnMwVqtwGplSmau6KR7uDFhJ4oWhu5NYUDTvZtxjTzPKznzLWM2THzPZ6gHJThVKugU148ZZySbp3vrGtb8EOdCevgKwokN0PVLtoPda9PfND+hYBMbwW35QzMa8eyJPlXghH9H9AuqhlRNrmPweF3Q6VBA/C4JEDHOmD0mu8wMzzaPnL8qjol7pL0pJPHGBzPvj524jw4reZnprE02u7ZTer0vhb8OpQm8GPEe/C4WKbX5e9izdiDBmfL3YSBMdo2NsvWBBboleQ2fKJdX7Crl/UsxTrSGGQqRfhwqxWcrp7VqgcfFStP051Xl0jZroKI56jRGygQGsNXYteujAY1LdLiDhPpyX6d3YwDGZsNLfT9EPD2c9yj5Fc/2qgeZKFHHi///Nm+MjAsZL0e5DrdBFDerH4zICoKDZkuZhRMypRLoQR/GvTH8g2mgNEc3kdRoBb89EyRP1Cg09Nzkhqcd1Ns0BSEdqRP0JoKEoKFToW5bXcx0JG7XF7yYs/et/3nsadOnf4P+pDrZG9TVBy1depou8rNtqSvgkraCzBPqet1P8swaY8eJCTkxDfU2pYEldE9MnzXZcKtIrD/aS31d8nN0Z51zjhLCZNuGaREgrkMrMknsG3wKXJREuruiX23y6doAt14XZYbokEfdN88wLCJn75xXfROJHtCEiAxyye0bqUWJtBwWeWIEM2EnBTAVPlg9okiMpW4meqSquVqpZpt9QyZztFnwFPpp/jVFTHwsAy+Tqxp5hT5evglVLsF+b1q+hRad0iywzXcyi85JZMLUgdBNCP8J8koGS1uejGdtK32ITv1P117qFWPjNQ96BFNlQl6R+YnztDtvQEpZrou5N6Ip7byABVTMSRFwjfL7s5l29xHYBFq08k0wFuE56quIquIA8VquN4VRtfIuzSzwnTusnlxMqZ8pfDqdqJbhNofMP+B+7WPz1/6Z3uC+LpI+91Kt4Iy9MkTzQnKPmpuWucI+DRctEZilpbno7LjsymJnofCHLj+6z+5qRruX7gY79zcKpmrbYJJwjc2k7lUDsWc7OdgOvbhV+RbwQAolWJVVxJSPnbBWUCFi/pIlI+LMzqctIf7RdyfirnuRjp5yRaGXS7k2sjVlOVrEdaTRxOGhJhChJaSsMM26DF5Bcm0dW4vzsJQOcWnyf98j/O5CLSikuBFLUx5Q4pe1XkO7JpkswUnaa/VV9RqiqOLcyILfJaeHEG0eS03bzoBSDQyxoSUMX5XAg1jsRqKxbR928PPTAXtbXQawtxmDxfBZuBZrHjHhlg79JJXvWbiK6kxOxExsLc6ZLCegrMOV8ujH3rxJX5d6Cb0HEfXeRb9eL1PaAsgqyrKFOUqdBP4rB/0r4gp12m+iq35wCzdK/sFYaqYyVt6o7kc2WtONIstL3Z2+bBl0zPLc+oufHHSfQDNdbggiQVg8CWY2i2O1mXGPRm15ipR9LBT1KvHxh4ZzPTvri7rhZ4ytr5bQBykSJ4JWWumKctLBIYfMsig65bygwXgrrR9P77bw1mMjo5xTbUbNvwJmqP/sbqaeQPilD6915mvT7ZL2Q8+ItQL4nV61pbeMDEtwgScXn78MIF/ZZLd3ZGAOikGbii+BhVXZNL30jqq8HwDE8RDhUEAZiIu2fjF+TMd6rNCyhCgrHLa+VIBP1miUjqMDwafQpCfKZVOzIy6PBY61gCPowooOJ/jLlTWHuCjO3j62WqR8a5ZhpUAiRx4zpkLxKTUsp5eV/h8VpUlePefkVWRs1oWaRi0MivMmh8sQekPfJOqF64ZKNAjsB/Kas5cv5xKZuQnUdCCt0nuW9jUgfgdYdZwpSbcQSIEMVaQamSp7iJaUQpARS7S8MeIMvhn74MeApxmR4MZgyBV5K5TaZ9R7WjelaBtWnCPojVbrxSLQ2+58cNSJEpyOB2LQ14iyFw9EM7TIGz3embQuqvXOXAW1jsNeovn3x3zxR3H6FgiY2kpwWPzCDmmpS3VkMBFpHipb/QqSp9NHLJkkpB4+gK0pXuTHKujE785skFuDANMRtvLPUX9oORTV75/RmqV1x2fv2/AfMIjnU57/UoaqW5zCJJZVJ9SxLnTn6xQkIX7hrS3/FSgVAY8OQT8w1IojfGLPBDzxtl2AQjRlq2nflenrcL9TpymsU9fIwW6CP8mKmMWCQNjlcVRhGrkmJhbjRxXbMm+apCofL1HR3uu134Qxb/oFECzzxyLfRgYUGd5HvYX96vUzim7u7XXw4lBhT2CMtqEjCuzPEUGbvAsUY8PimSLRkHq7v6a8xoYGzA64nsS89R+PspmGKr5qLUcZa/KA+D+JyluGvsrbUF3pNvtxtM+IteCts+YHbSXKPV+V9kMfFPcEpdtjxRsKZeYmEWqAlOmJl7CVzY4S/FlXtueJzEnvE2bmCuTqrJOI/XJGD3aAC5To55/p8IKobusgpye+cAA8W25x9xc2W7myQxSoxUeel9Da/VV4s2oLzmYVFlfKsP2ZxS2Mx26bdPmBv9XwdOcDXJF6GYANLaWrCx65y2GGh/Zx/bdEaWlbirUJxCmcJfs5qapqt62QX/Zgtk/brn2k6lZyuLvB1t28L7Rtho/5AuIp7qfJ7aekMRKaIKwC/2khTLQK1wjJe5Jz188rLccp7vVgTyRQpbRHP9/YLMxZoXlnHN2EyWWlg2avSbU6RGFCU8zUH+F501hm+KK1yr4o20I+qI7ZQTrK/H7+KU7u9kl5ft4OgUEvFEP5wuvN+Oa3TMGbQUnSARrnhM6Qj7hHTJoA9+o9XkYiP5LCJsh3Y2+bqU3Caq7hQtwrKf1gJHf5B9G9vLYQml81/thoLMQc7pz9pyTQMKxSj4q3jxN6YXFccs+T8FcZll/NFJQ0R+7qaq0okqzM1Cc+HaS1D/Ruapi+UIX6KzOUV4gTYFn3fxgHkrhedeiqitevKIqmXC4szrn9utoYxI6qRyfDPWqZgLHK1PP0djK1nu6Q6WCGBCiEiSJxNeexupIpWXxr9AKOhXcusASuCi5UmmySaSgPfM+oO0lk7hr6dqFrehV831178rJt0mYWiYDrcXiuj32MiDZS5YAQ+KCNyr/uQul6QxX3ZJnH9p3Li82Y71p/62pjE1oT0MdM1TBCrW2r7UCcVm4h30jOTkzKSrCWeoviTjkBOgbJlAmWmB53un0oyIqkXeE6+Gr8xYNqNCgs/1uKI840U5QYDb5WTxXI7ZRqfgLtgw292sBWonojrMivMwc2RtEao5QbmX1tBiOmhU0uHkGhGAv4dR9fBrOy65ehmV4IVHcu02mQpm64FddFYhNwqMfPA/RJslSvLoTCEf6gpTz2tinkMtzElEYz/eLtDs70d8Qka4mbVKZTiZoP5TdsxnjSZ3lnaMxbnQ8z9M5uDKxzjaRkuFDwXKiL/eQbOaHXV4Cf8N+7lN9wKuJJAEu2cjl7Pi/EraPu2dSisrAOp/hzL+BGE6c219D0RbxyVuYHl1pirYPsWNSTB0tWD4AjgiqMEZSV/xLf0D9UkNHMU++jrcUQd8Hrl/HxQ/xtCKdfyOd1u22ZgJk8l5L2qu8qsjsLZPBrJVt42VtCwusUbDbnZ8Q0Ieh+DVssxRcVoJG3AMpKI7/QIFjiJAVhILmdkfbPyFH2sgoP5jfos3eGHlUBJIjiObiYYVhq2EyadGeo1s9NK78fDlFKmmlDO8BF0hKVHrDh+3mVPvWrDQGkfMG3k5EO12Q+2xknKW6Brf+CjIkGU/PbiDhb7FQ+ifNfYK95F/baB1/h2NSipfgpt0bkfRljFV+fz7tnryA35EZFvi9HLjqMg5qce+McNPHj8ENuhTQLhRWhlP1rQtmpIZ1EPzhQ4ULND4CF9QAZ37lM6CoPzU7jIAfO4zInFMnLMELmmW5fm27lNd5vXiokuh6hNyc+QnsAB1tDI9YJh90w+Kgnm9VzBfyilxE+PrOmUgd6hUN2xdA+mm/7fq94t9W/3VePKjUYGG0dRoDV+Vff/gE9Nv+pGuoGdbGyHTcQRExTNJkfi7H7NCK7sBluLBEQzdaPlg1iv/DureMM92QXiwUWCztdhtO2IVit5tbUvV08EElNBm74ty15l58igGGZ/Yd1zHhNaXOoi7oimogE5uP4zNmkT35ZV27Otvbo2NiJgxVr6hI4KaUyPo4YjyGc6mg1M4i3Sw4c1HBAg2xSFrALWTD/hExlwO6p8eT9sE84JVJU/0FXWcsqBoP+UhO5m8OLj2pt343sBOZIS/AeEenfIdLdIQ0ezOirk92cdYi8m80rfH+DHisfVHjdTCVzuvhBKcL9Bt8e2N+IAPKi4iboocpdy4D8ZqpSVGmqbB+/WGZnEfR2+KRRSvIRNicVugvaosDmeVbt6suqpjqQOkdjRy/3munLUJzOyJIZ2MaVzCRQzfjLRRaR/3SR+wSzoN4sfJUIWAmv7Mkk+pGWlJANtqpO3rOx7hogpuSpZCnZihZ7+3V4aedSku8WqxFBuoFt6ERDk6cGHKG70O0XwThpP+KdMtTpGCVwwiI1DohymABILz087Jw0OtwBaLwInAJ0sBm/J6GfaYDj9AGXYxMhco4x/Ukf5h31pJutNlXsm6g8osgNBvFu65knbQp2k1Aj+Vgx8HYyUvPq/nhmxMd60iStmmrIyFnyzd7fWBRGGnYG8j2ZQUQ+TwJ+C4/UlN+YD6i58RnC+EJVHrgTPGe2ijxFL9kvXY1OUcI5Vz8ozMXee1jnRopnfniHCBPUi6IumyBKhkW1CwVDt7pF5cxORaBBU+pT5Gv6CLyl5qW7a6vItO1B04sFVOiSvBREEYY/wpdbuCZWgeVLgJPxzgvtGP23HHojnu6+YKBzliFsKcmk4c1KW6ZVjUKRdPx7WjMMs0JswbKOqRpeJFvpeq6uewieNfWsN0/JOSHbGQ0rAvxcDaj+v3g0ArArnxkYgP6ToUxsMnngMkow3GhpWWkIbTZjL7pYvFlpMx55hXBrXmhGMqirBeUaQccbEBqfvml5o8OnFM3vx7IE47a82FLNCluxrfcnUjdfjBhddHAkKzNWz+wfD6jY9jncCN6xTxjJHYghTYlkZmSClQjsHUM78dDe7cWlZB6capKfKCd5Oy+0OEk+f7VCGuc/iw1elpD1MKhev39np9sX5e0vx/GoF6Df78TdRrC9eKGgSuIpecH5LLnWidZhPZymEQsmrRbkVetEdWr7lNPQZ2AGAj2z9cQGXYEfWkEHrdMy8np88qQB6xHZoitNW7Mdtql41WBitd48klz4sGWpb5spiamiRXWPIla6Etx4v7ci/kf6W4Gzh4ISxMt7J5nJZ06GIJ0A40DNo7hLDvlqtaOT5Aqz0QLclBsv1A==
指向原始笔记的链接
3.1.1. 小信号模型
BJT
Transclude of BJT#共发射极的射频双极晶体管的小信号等效电路模型指向原始笔记的链接
3.2. HBT
Transclude of HBT
3.3. FET
FET
FET
场效应晶体管(field effect transistors)是一种通过电场效应控制电流的电子器件。它依靠电场去控制导电沟道形状,因此能控制半导体材料中某一种类型载流子沟道的导电性。
分类
场效应晶体管可分为 JFET 、MISFET 和 MESFET。
指向原始笔记的链接MESFET
MESFET
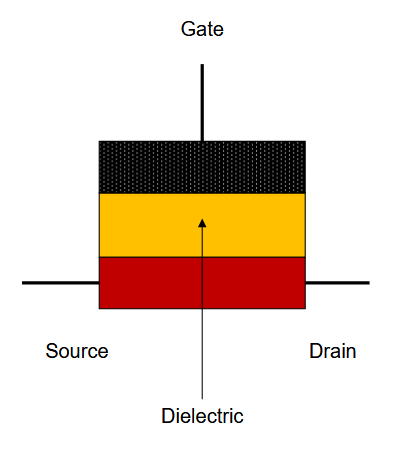
结构
上图是典型 n 沟道砷化镓 MESFET 的截面图。栅极结形成肖特基势垒。这种晶体管具有理想的增益和噪声特性,原因是砷化镓比硅具有更高的电子迁移率,并且不存在散粒噪声。
工作时,电子被正
电源电压从源极引向漏极。随后,这些多子被施加在栅极上的偏置电压 进行调制,产生电压放大。最高工作频率受栅极长度限制 : 目前 F E T 的栅极长度为 ,相应的上限频率为 。 共源极小信号等效电路模型
产生的电流
取决于栅极-源极电容器 两端的电压,在正常工作条件下 (其中端口 1 为栅极,端口 2 为漏极)。由 给出的反向信号仅通过电容 传输。从上述数据可以看出,该电容值通常很小,在实际应用中经常被忽略。此时 , 是单边器件。 工作上限频率
和 BJT 类似,我们可以使用上图的等效电路模型来确定 MESFET 的工作上限频率。对于场效应晶体管(FET),短路电流增益(
)被定义为当输出短路时,漏极电流与栅极电流的比值。在单向传输的情况下,即 时,短路电流增益为, MESFET 共源小信号等效电路短路电流增益计算式
对于单边情况,即
时, 指向原始笔记的链接 上限频率阈值
(此时短路电流增益 )由下式给出, MESFET 共源小信号等效电路上限频率阈值计算式
当短路电流增益
时, 指向原始笔记的链接 MOSFET
Transclude of MOSFETHEMT
Transclude of MODFET指向原始笔记的链接
4. 滤波器
第 8 章 微波滤波器
采用插入损耗法设计滤波器
理想滤波器具有一下的特性:
- 插入损耗为 0;
- 阻带内的衰减无穷大;
- 通带内为线性相位响应。
相较于镜像参量法,插入损耗法的优点在于:
- 存在明确的改进设计的方法;
- 是一种系统的方法;
- 可以计算出必要的折中。
用功率损耗比表征
用功率损耗比表征滤波器响应
1. 表征方法
1.1. 用功率损耗比表征
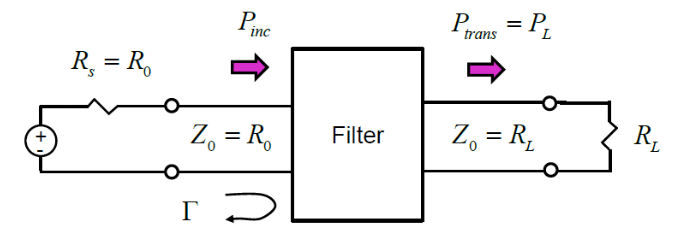
在插入损耗法中,无损滤波器的响应由滤波器的功率损耗比来定义:
插入损耗计算式
指向原始笔记的链接 1.2. 用插入损耗表征
用
表示的插入损耗为: 用 dB 表示的插入损耗
指向原始笔记的链接
为功率损耗比。 1.3. 用 S21 表征
我们还可以用
来定义插入损耗。如果该网络的负载端口和源端口均匹配,则有: 插入损耗 S21 定义式
指向原始笔记的链接 用
来表示就是, 如果滤波器是无损的,则能量转换:
1.4. 用反射系数表征
由于
是 的偶函数,它可以表示为 的多项式,因此可以将其变换为, 其中,
和 是 的实数多项式。代入功率损耗比定义式即可得到, 用反射系数幅度计算的功率损耗比
指向原始笔记的链接
和 是 的实数多项式。 注意,指定功率损耗比的同时也限制了反射系数的幅度
。 2. 最平坦响应的表征
最平坦响应
该特性也称为二项式或巴特沃斯响应。在给定的条件下,该响应能提供最平坦的通带响应。
对于低通滤波器它的插入损耗满足:
指向原始笔记的链接最平坦响应的插入损耗
指向原始笔记的链接
为滤波器的阶数; 是截止角频率。一般来说,设定在截止频率处,插入损耗为3dB,因此通常选择 。 3. 等纹波响应的表征
指向原始笔记的链接等纹波响应
若将切比雪夫多项式运用于 N 阶低通滤波器的插入损耗响应,则会得到陡峭的截止响应和幅度为
的纹波。 等纹波响应的插入损耗
指向原始笔记的链接
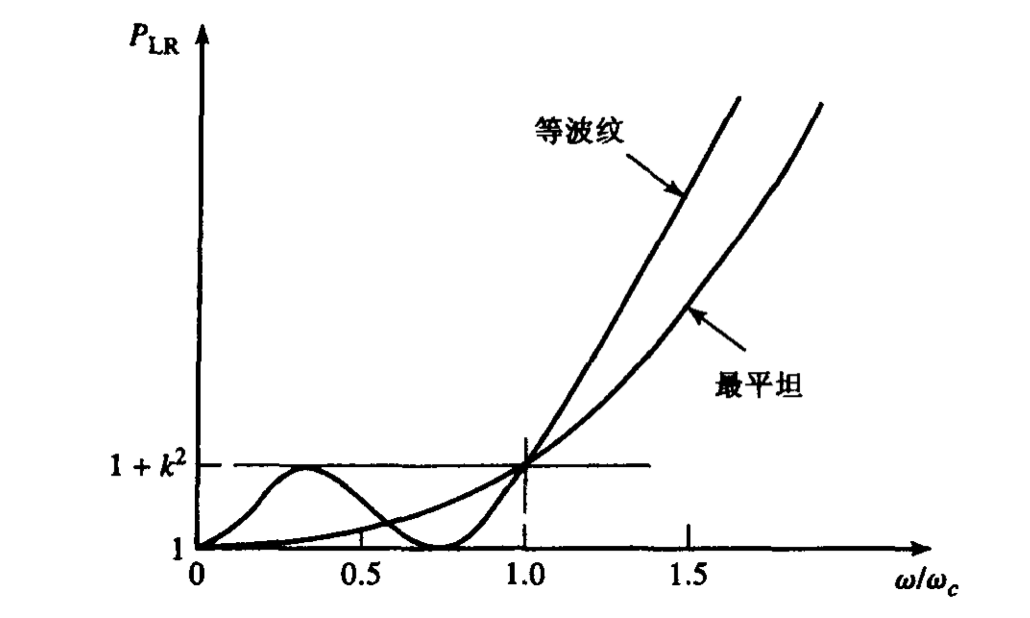
为滤波器的阶数; 是截止频率。一般来说,设定在截止频率处,插入损耗为 3dB,因此通常选择 。 该特性在通带内会有一个幅值为1+k2的波纹,不会像最平坦响应那样在通带内具有平坦的特性,但是等波纹特性的滤波器在截止频率处变化更陡峭,更接近理想低通滤波器特性。
指向原始笔记的链接
最平坦低通滤波器原型
最平坦低通滤波器设计
对于归一化低通设计,其源阻抗是
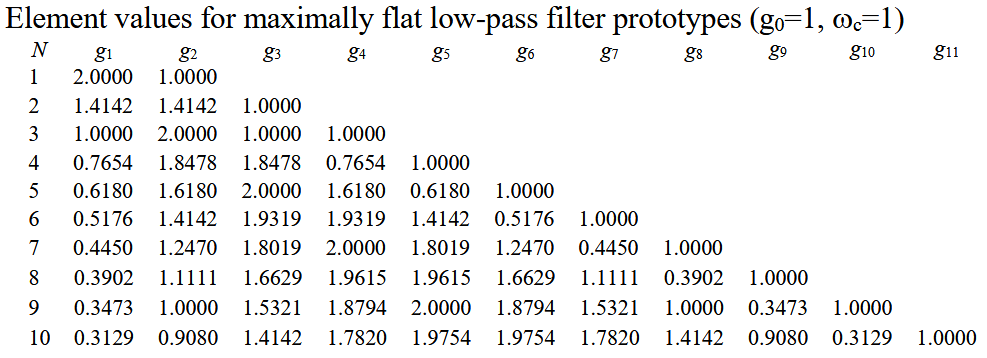
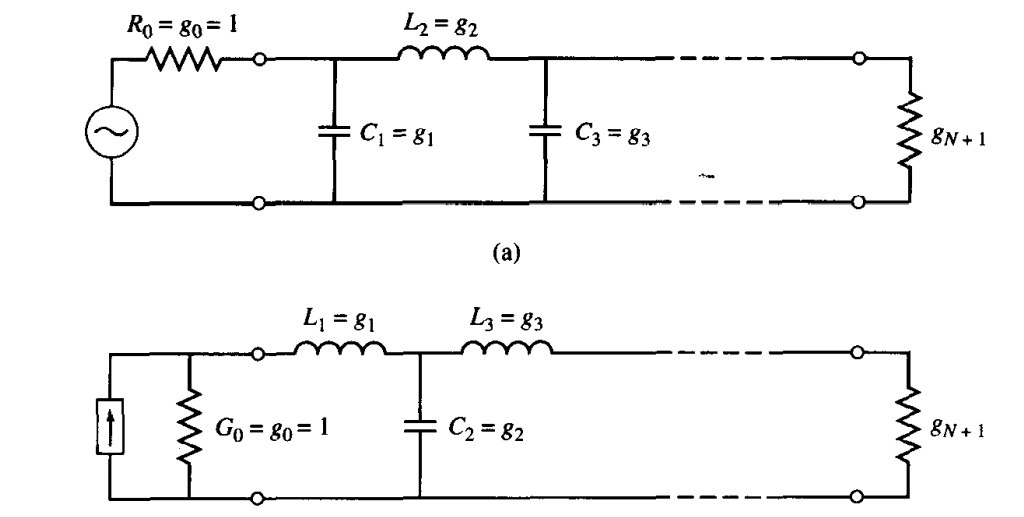
,其截止频率为 ,并且 。由此构建的 N 阶梯形电路的元件值已经被制作成表格。
1. 电路选择
对于一个最平坦响应的低通滤波器,我们可以使用以下两种通用电路:
从信号源开始,我们可以选择第一个元器件为并联还是串联,之后的元件串并交替,两个电路均能够实现相应的功能。
第一个电抗性元件为电容的称为
(pi)型电路,第一个电抗性元件为电感的被称为 (tee)型电路。 Question
串并联之间有什么区别吗,会影响什么性能呢? 答:无区别,互为对偶,两者给出同样的响应。
对于有
个电抗性元件的滤波器,这些元件值已编号为从源阻抗 到负载阻抗 。这些元件在串联和并联之间交替出现,且 有下面的定义: 源 电 阻 源 电 导 到 串 联 电 感 器 的 电 感 并 联 电 容 器 的 电 容 负 载 电 阻 , 若 是 并 联 电 容 负 载 电 导 , 若 是 串 联 电 感 于是,上图所示的两种电路就可以认为是互为对偶的,两者给出同样的响应。
2. 阶数确定
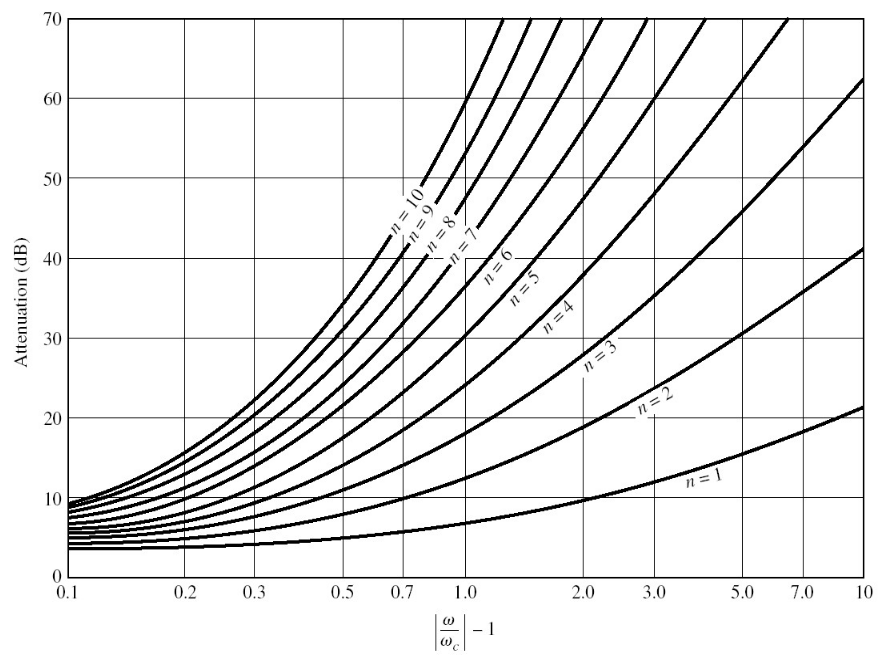
给定固定频率时的插入损耗值,我们可以根据下表确定滤波器的阶数:
一般题目会给出要求,例如“在 2GHz 时插入损耗至少为30dB”,题干中又给出截止频率为 1GHz,这里
指向原始笔记的链接,再减去 1 之后就等于 1。如果想达到 的衰减,按照曲线而言则至少需要 5 阶。5 阶就意味着需要 5 个集总元件。 等纹波低通滤波器原型
等纹波低通滤波器设计
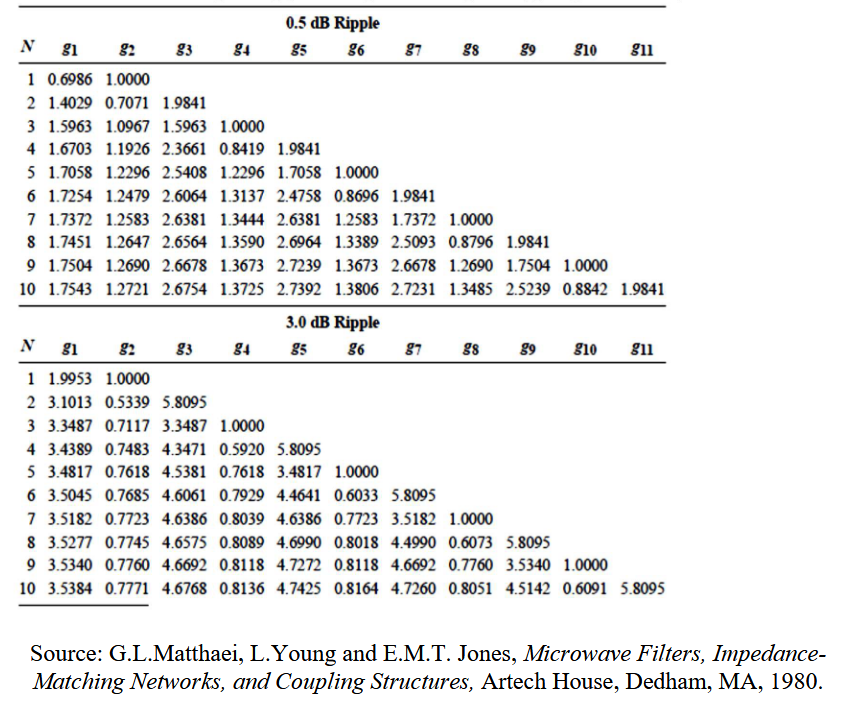
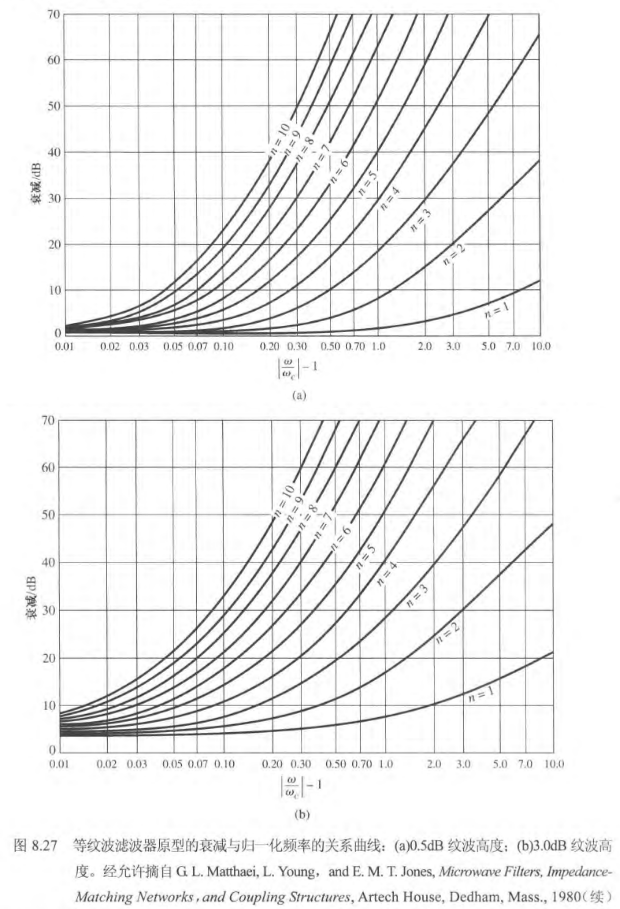
对于归一化低通设计,其源阻抗是
,其截止频率为 ,并且 。由此构建的 N 阶梯形电路的元件值已经被制作成表格。 [! attention] 注意,负载阻抗对于偶数
有 。 等纹波滤波器一般分为两种:带内纹波为 3dB 和带内纹波为 0.5dB。
电路结构
电路基本结构和 最平坦低通滤波器原型设计 是一样的。
确定滤波器阶数
通过下图,我们可以知道多少阶的滤波器可以满足我们的需求。
确定阶数之后,即可在「等纹波低通滤波器原型的元件值」表中查找原型器件值。
指向原始笔记的链接滤波器变换
前一节介绍的低通滤波器原型是源阻抗
和截止频率 的归一化设计。下面说明这些设计如何根据阻抗和频率来定标和转换,以便提供高通、带通或带阻特性。 阻抗定标
阻抗定标
在原型设计中,源电阻和负载电阻是归一化后的。唯一的例外是具有偶数阶的切比雪夫滤波器,其负载电阻具有非单位值。如果设计的源电阻不是 1 而是
,则原型电路的所有阻抗都应乘以 。若令带撇号的符号表示阻抗定标后的值,则可给出新的滤波器元件值为, 低通滤波器原型到设计滤波器的阻抗定标计算式
指向原始笔记的链接 频率定标
低通滤波器原型到低通滤波器的频率定标
要将低通原型的截止频率从 1 变为
,需要乘以因子 来定标滤波器的频率。这是通过用 代替 实现的 从低通响应变换到低通响应的频率代换
指向原始笔记的链接 低通滤波器原型到低通滤波器的频率定标电抗性元件值计算式
指向原始笔记的链接
和 为低通原型滤波器电抗性元件数值; 和 是频率定标后电抗性元件数值; 为截止频率。 低通滤波器原型到高通滤波器的频率定标
和低通一样,首先做频率的代换,
从低通响应变换到高通响应的频率代换
指向原始笔记的链接 将
映射到 ,反之亦然;截止发生在 时。要将电感 (或电容 ) 转换为可实现的电容 (或电感 ),负号是必需的。新的元件值为, 指向原始笔记的链接 低通滤波器原型到带通滤波器的频率定标
首先做频率的代换,
从低通响应变换到带通响应的频率代换
指向原始笔记的链接
和 是通带边界; 是通带的相对带宽,中心频率 可选用几何平均 。 新滤波器元件又串联电抗和并联电纳确定。
串联电感
被变换为串联 LC 电路,其元件值为, 并联电容
被变换为并联 LC 电路,其元件值为, 指向原始笔记的链接 低通滤波器原型到带阻滤波器的频率定标
首先进行频率的代换,
从低通响应变换到带阻响应的频率代换
指向原始笔记的链接
和 是通带边界; 是通带的相对带宽,中心频率 可选用几何平均 。 低通原型的串联电感被转换到并联 LC 电路,其元件值为,
低通原型的并联电容被转换到串联 LC 电路,其元件值为,
指向原始笔记的链接
5. 放大器
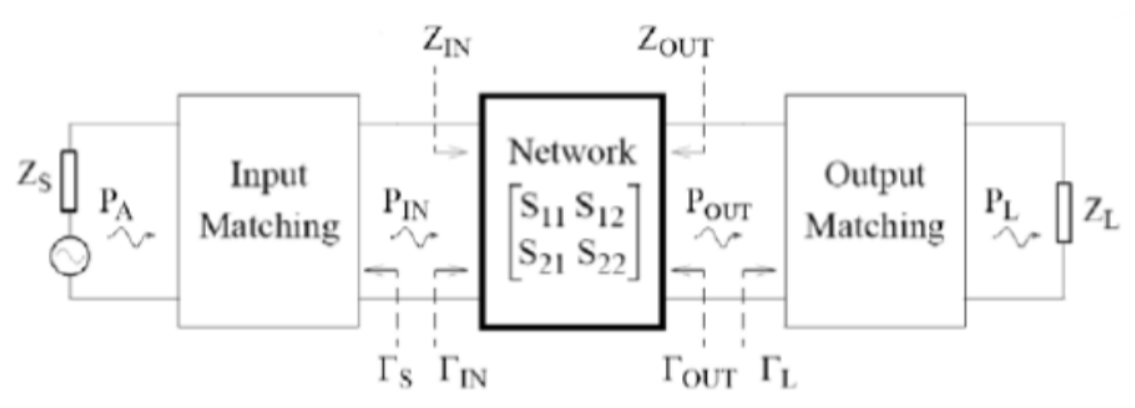
第 12 章 微波放大器设计
1. 二端口功率增益
本节根据晶体管的散射参量推导几种常用二端口放大器的增益和稳定性公式。这些结果将用在随后几节的放大器和振荡器设计中。
1.1. 二端口功率增益的定义
后面根据二端口网络的散射参量以及源和负载的反射系数
和 来推导三类功率增益的公式。 首先通过定义,我们可以得到源和负载的反射系数,
随后计算看向端接网路输入端和输出端的反射系数,
看向端接网络输入端的反射系数
指向原始笔记的链接 看向端接网络输出端的反射系数
指向原始笔记的链接 [! note] 上面这两个公式非常好记,都是从反射电压波推导出来的。以看向端接网络输入端的反射系数的计算式为例子,首先用 S 参数矩阵乘法表示出反射电压波,然后用负载的反射系数去代换 2 端口的电压即可。
三种功率增益
实际功率增益
实际功率增益
实际功率增益
是负载 功率与输入到双端口网络的功率 之比。这种增益与源阻抗 无关,尽管有源器件的特性可能依赖于 。 实际功率增益计算式
指向原始笔记的链接
是负载耗散的功率; 是双端口网络输入功率。 资用功率增益
资用功率增益
资用功率增益
是双端口网络可用功率与源可用功率之比。这假设源和负载都进行了共轭匹配,并且依赖于 ,但不依赖于 。 资用功率增益计算式
指向原始笔记的链接
是双端口网络的输出功率(资用功率); 为源的资用功率。 资用功率增益与源端匹配、放大器的S参数有关,与负载端的匹配无关。
指向原始笔记的链接[! faq] 资用功率增益隐含了负载与输出匹配网络共轭匹配这个条件? 可以这么理解,因为在负载与输出网络共轭匹配的情况下,
转换功率增益
转换功率增益
转换功率增益
是传递到负载的功率与源可用功率之比。
转换功率增益计算式
指向原始笔记的链接
是负载耗散的功率; 是源资用功率。 看向端接网络输出端的反射系数 #挂起/信息不足
转换功率增益与源端匹配、负载端匹配和放大器的S参数都有关系。其是在输入和输出都匹配时发生的一种特殊情况,即零反射 (不同于共轭匹配 ) 的一种特殊情况。这时有
, 转换功率增益简化计算式
条件:零反射 (不同于共轭匹配 ) ,这时有
指向原始笔记的链接 单边转换功率增益
还有一种特殊情况,就是当
或者小到可以忽略的时候,就能计算单边转换功率增益。 单边增益
这里给出转换功率增益的两种替代表达式,包含输入反射系数或输出反射系数。对于单边设备,其 S12 = 0 (没有从端口 2 到端口 1 的反向传输),则
且 。转换功率增益的两个表达式都可以简化为以下单边转换功率增益等式 单边转换功率增益计算式
条件:
指向原始笔记的链接 单边最大转换功率增益
当器件为单边器件时,并且源和阻抗都共轭匹配了,即
且 ,这时有, 单边最大转换功率增益计算式
条件:
,且有 和 指向原始笔记的链接 三种功率增益在实际设计中的参考作用
指向原始笔记的链接
- 在选取放大器时,需要根据设计要求,选用合适的管子,这一般是放大器设计的第一步,这个时候,就需要参考实际功率增益。
- 如果是设计 LNA,除了增益以外,稳定性和噪声也是一个很重要的指标,而对于 LNA 来讲,外接的负载一般是 50 欧姆。所以,LNA 的设计,我觉得输入匹配网络的设计更为重要,因此更多的是参考资用功率增益。但是因为放大器的输出,一般都不是 50 欧姆,输出网络匹配也需要设计,这个设计,更多的是共轭匹配的设计。
- 如果是设计功放,需要输入输出都共轭匹,且输出一般会有一个最佳工作状态 (load pull),因此这个时候,更多参考的是转换功率增益。
1.2. 二端口功率增益的深入探讨
对于放大器设计而言,最有用的增益定义是转换功率增益公式,其考虑了源和负载均失配的情况。于是可以将输入匹配网络、晶体管本身以及输出匹配网络的有效增益系数定义,
源匹配网络有效增益系数定义式
指向原始笔记的链接 晶体管有效增益系数定义式
指向原始笔记的链接 负载匹配网络有效增益系数定义式
指向原始笔记的链接 于是总的转换功率增益就能写成,
总转换功率增益定义式
指向原始笔记的链接
是源匹配网络转换功率增益; 是晶体管转换功率增益; 是负载匹配网络转换功率增益 接下来我们考虑单边的情况,
单边增益
这里给出转换功率增益的两种替代表达式,包含输入反射系数或输出反射系数。对于单边设备,其 S12 = 0 (没有从端口 2 到端口 1 的反向传输),则
且 。转换功率增益的两个表达式都可以简化为以下单边转换功率增益等式 单边转换功率增益计算式
条件:
指向原始笔记的链接 而要决定是否使用单边转换功率,我们还需要看单边转换功率近似品质因子,
单边增益近似品质因子
实际上,S12 通常非常小,因此我们需要一个品质因数来决定是否可以使用单边增益近似,
单边品质因数
指向原始笔记的链接 通过使用以下关系,单边品质因数可用于确定在设计过程中使用
而不是 而导致的最大误差: 通常,如果由
指向原始笔记的链接比率定义的增益误差在 ±10% 之内(即 U < 0.05),我们就可以使用近似值。 2. 稳定性
下面是有关晶体管放大器稳定工作的必要条件的讨论。
稳定性条件
如果在二端口网络的输入端或者输出端阻抗中存在负实部(
),使得 或者 ,则可能导致电路振荡。 又因为这两个反射系数和源以及负载匹配网络有关,因此放大器的稳定性取决于匹配网络给出的
和
定义两类稳定性:
- 无条件稳定。若对所有无源信号源和负载阻抗有
和 ( 和 ),则这个网络是无条件稳定的; - 条件稳定。若只对某些无源信号源和负载阻抗有
和 ( 和 ),则这个网络是条件稳定的,也称作潜在不稳定。 [! note] 对于单边器件而言(
),当满足 和 的时候,器件无条件稳定。前者是后者的充分条件。 2.1. 稳定性圆
因为对于放大器的稳定性的检验的本质是对匹配网络的
和 进行的检验。 输入稳定圆计算式
指向原始笔记的链接 圆 心 半 径 输出稳定圆计算式
指向原始笔记的链接 圆 心 半 径 器件无条件稳定时,稳定性圆必须完全位于史密斯圆图的外部 (或完全包围史密斯圆图 )。用数学公式将这一结果陈述为,
2.2. 无条件稳定的检验
2.2.1. Rollet 条件及其辅助条件
同时满足,则可以证明器件是无条件稳定的。这两个条件对无条件稳定是必要的和充分的,如果不满足,那么就不是无条件稳定;如果存在使其稳定的Rollet 条件及其辅助条件
无条件稳定的Rollet 条件为,
辅助条件为,
当不满足的时候,为潜在不稳定状态
指向原始笔记的链接和 值,那么就需要用稳定性圆来确定。 器件无条件稳定的时候,必定有
和 。 rollet 条件不用用来比较器件之间的稳定性。
2.2.2.
参量 mu 参数稳定性检验式
指向原始笔记的链接
为 S 参数的行列式; 大于 1 的时候无条件稳定。较大的 意味着较大的稳定性
6. MMIC
MMIC
%69a71eb06c7d7f194925f14bb5320000dcc4f97ea4d7c34abc263cd578ca835aMdP7F1DZfEouHp/TrktTA3jPdyqvQttXWpGR8nIDFit4NyTzs6UEFyT+1CIX72NRmk9mzDN9+S8BCPMkdDyoLLag0MhCVSIx7+CTul7CDWbP56LCjejk0aneZkSW7izFhU9zm5DcZ4QfzBoFZ1OJ3Oj2SmCvt6oLt12eue6SgIIb0/9p/bNjU7Pi8muAMQ==
指向原始笔记的链接

.png)