[! tldr] 这一章的主要内容是介绍了传输线理论并且将电磁理论运用到对传输线的分析上面。
通过电报方程求解在传输线上传播的波的波方程,然后对波方程进行求解得到波阻抗、相速度、波长。
传输线是由传播常数和特征阻抗来表征的。然后拓展到无损以及高频低耗情况下的上述参数。随后我们考虑了无损传输线端接负载的情况,考虑了端接负载所引起的波反射以及如何计算反射波和损耗以及度量传输线的失配量的参数,即反射系数、回波损耗和SWR。随后学习使用史密斯圆图对电路进行分析和匹配。
传输线的集总元件电路模型
电路理论和传输线理论之间的差别
电路理论和传输线理论之间的关键差别是电尺寸。电路分析假设网络的物理尺度比电波长小得多,而传输线的尺寸可能为几分之一个波长或几个波长。因此,传输线是分布参数网络,在整个长度内其电压和电流的幅值与相位都可能发生变化。
传输线方程
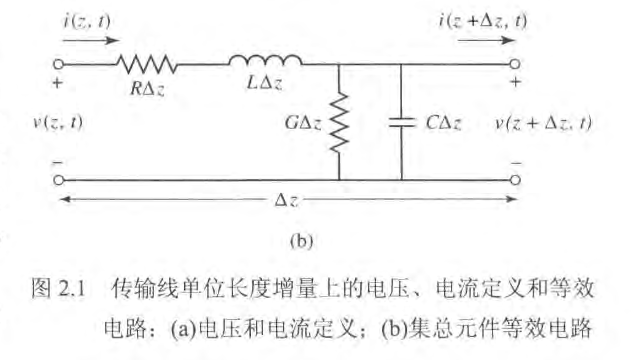
上图是传输线可建模为上图中的集总元件电路,其中的参数都是单位长度的量。
串联电感
通过使用基尔霍夫电压定律和基尔霍夫电流定律进行分析,能得到电报方程的时域形式,
电报方程时域形式
指向原始笔记的链接
传输线上的波传播
通过联立电报方程得以求解关于电压电流的波方程,然后求出其行波解,
通过将特征阻抗
传输线特征阻抗定义式
指向原始笔记的链接
为两个传输线导体的有限电导率产生的电阻; 为传输线两条导体总自感; 为传输线两个导体间填充材料的介电损耗; 为传输线两个导体靠近产生的电容。
以此联系传输线上的电压和电流。
根据 波方程和基本平面波的解 这一节的内容,可以推断出传输线中传输的波的相速度和波长。
无损传输线
在实际情况中,传输线的损耗可以忽略,由此传播常数和特征阻抗都可以近似为实数。
同样可以简化特征阻抗、波长和相速。无损传输线的传播常数计算式
其中,
指向原始笔记的链接; 为角频率; 为单位长度电感; 为单位长度电容。
无损传输线的特征阻抗计算式
指向原始笔记的链接
为传输线单位长度电感; 为传输线单位长度电容。
无损传输线的波长计算式
指向原始笔记的链接
是传播常数的虚数部分; 为传输线单位长度电感; 为传输线单位长度电容; 为角频率。
无损传输线的相速计算式
指向原始笔记的链接
为角频率; 为传播常数的虚数部分; 为传输线单位长度的电感; 为传输线单位长度的电容。
端接负载的无耗传输线

上图画出了一个端接任意负载阻抗
假定有一个形式为
传输线上的总电压
指向原始笔记的链接
传输线上的总电流
指向原始笔记的链接
为什么在考虑反射波的时候,电压相加而电流相减?
需要注意平面波的通解的内容。平面波在介质界面反射的时候,电场强度方向不变,而磁场强度方向则会转
,而电压是电场产生的,电流则是磁场产生的。因此会有不一样的变化。
将负载上的总电压和总电流通过负载阻抗联系起来,在
由此可以求得反射波。入射电压波振幅对反射电压波振幅的归一化,定义为电压反射系数
用波的形式表达就是,
Note
这里需要对电压反射系数有个更深入的理解,为什么电压反射系数的范围是
。首先,电压是以波的形式存在,由于能量守恒定律的存在,在考虑波的反射的时候,不会有更多的波产生,于是振幅绝对值的最大值为「1」。其次,为什么会出现负数,负数意味着电压振幅产生了反向。
于是线上的总电压和总电流可以写为,
从这些表达式可以看出,线上的电压和电流是入射波和反射波的叠加:这样的波称为驻波。只有当反射系数为 0 的时候,才不会有反射波。若
当负载失配时,不是所有来自源的可用功率都传给了负载。这种“损耗”称为回波损耗 ( Return Loss, RL) ,它定义 (以 dB 为单位 )为,
负载匹配(回波损耗定义式
指向原始笔记的链接
为回波损耗,单位为 ; 为输入功率; 为反射功率; 为反射系数。
当负载匹配的时候,传输线上的电压幅值
根据相位项
由描述传输线上变化电压幅值的公式可以看出,两个连续电压最大值 (或最小值 ) 之间的距离是SWR 定义式
指向原始笔记的链接
为反射系数。
电压的振幅是随着线上的位置而起伏的,由此可以知道,线上的阻抗也必定随位置变化。在距离负载
这个公式给出了任意负载阻抗的一段传输线的输入阻抗。传输线阻抗方程
指向原始笔记的链接
为输入阻抗; 为反射系数;
Smith 圆图
史密斯圆图提供了一种使传输线现象可视化的方法,学会如何用史密斯图来思考问题,就能直观地求解传输线和阻抗匹配问题。
史密斯圆图
史密斯圆图是一个用于辅助设计的工具。
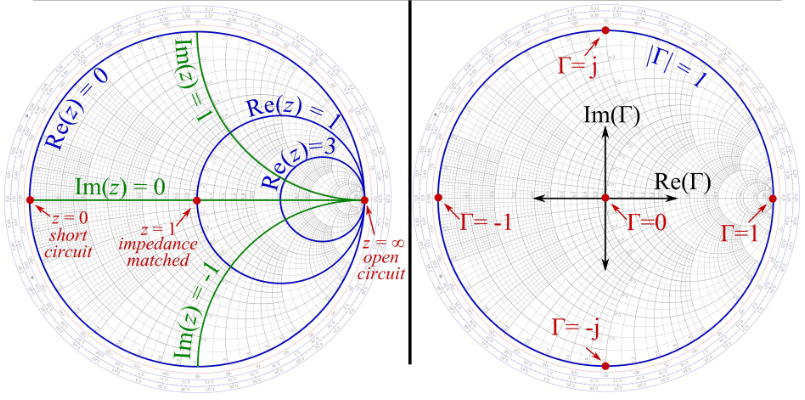
史密斯圆图的构成
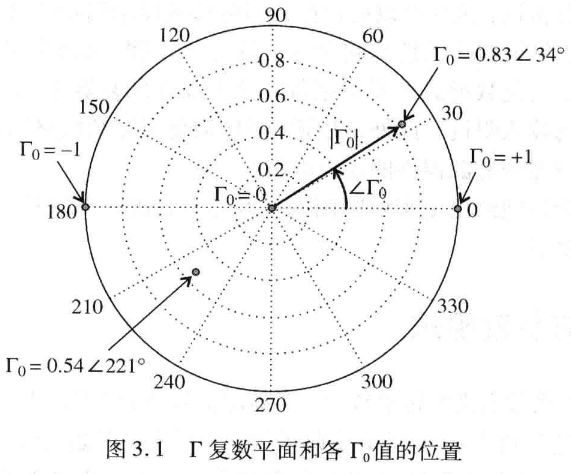
史密斯圆图基本上就是一个电压反射系数
的极坐标图。 首先,把反射系数用幅值和相位(极角) 的形式表示为
。然后把幅值 画成从图中心算起的半径( ) ,把角度 ( )画成是从水平直径的右手边算起的角度。任何无源的可实现的( )反射系数都可以在 Smith 圆图上画成一个唯一的点。 归一化阻抗点
史密斯圆图的真正有用之处是画在图中的阻抗(或导纳)圆,阻抗(或导纳)圆可用来将反射系数转换为归一化阻抗(或导纳),反之亦然。处理图中的阻抗的时,通常用归一化的量。
归一化阻抗计算式
指向原始笔记的链接
为线路的负载阻抗; 为传输线的特征阻抗; 为传输线电阻; 为传输线电抗 根据归一化阻抗即可在史密斯圆图上找到对应的点。归一化阻抗的实数部分对应电阻圆,虚数部分对应电抗圆。
归一化阻抗点与圆心的距离,对应到史密斯圆图的水平标尺
TRANSM.COEFF,E or I即可找到对应的值(注意起始点的位置)。 也可以根据以下变换公式, 将归一化阻抗转换为复反射系数
映射到史密斯图上: 归一化阻抗导纳到反射系数的变换公式
指向原始笔记的链接
为归一化阻抗; 为归一化导纳 计算出的
即为对应的坐标,通常用极坐标表示。
通过这个转换, 可以将复阻抗
平面上的每一个点, 映射到史密斯图的 平面上。这实际上建立了两个复平面之间的一对一映射关系。这就是史密斯图的定义。它实现了从复阻抗平面到复反射系数环形坐标系的转换, 并建立了二者之间的映射对应关系, 以此来分析和设计微波电路中的匹配网络。
史密斯圆图的应用
史密斯圆图的应用
基本运用
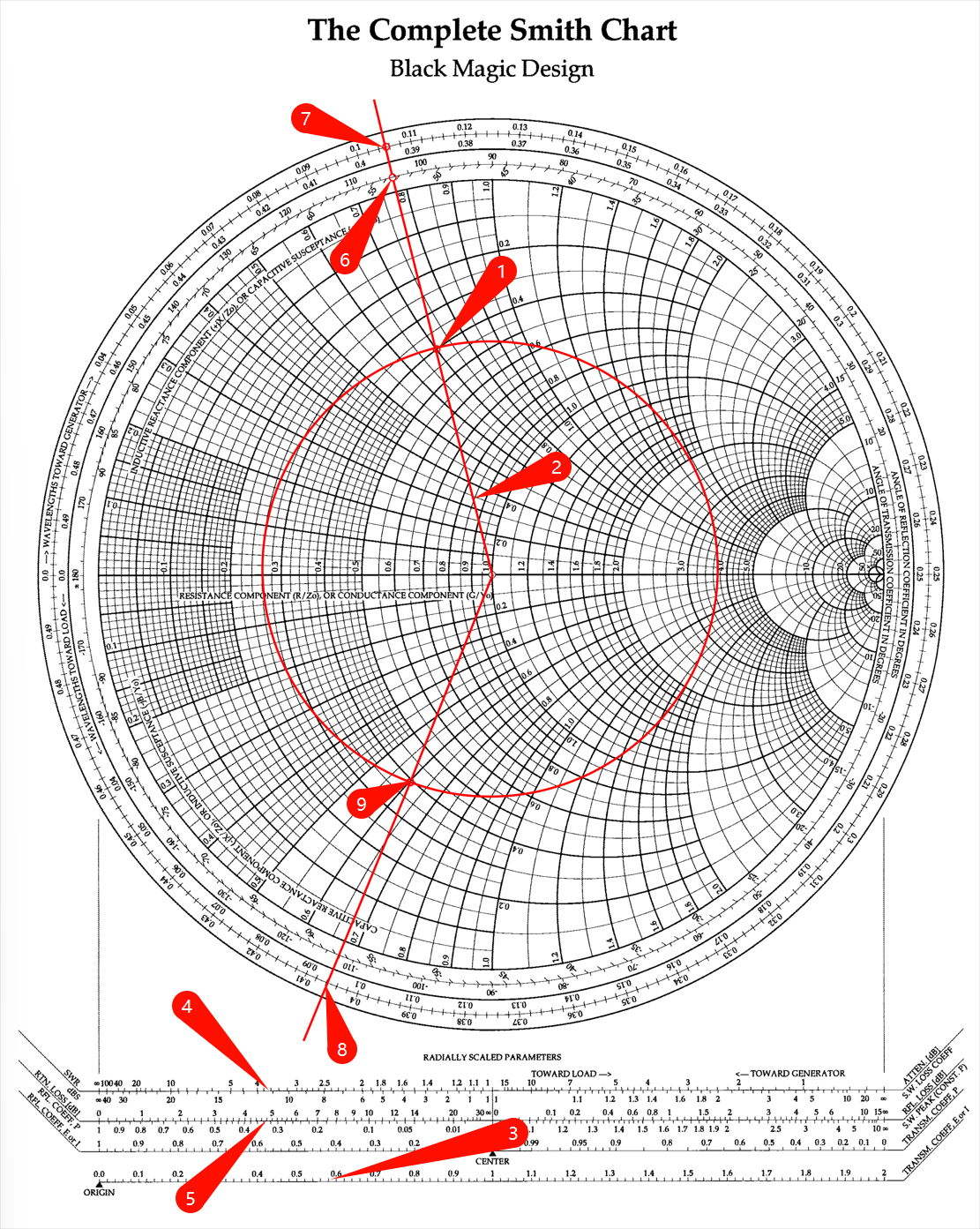
求解负载处的反射系数、传输线输入端的反射系数、输入阻抗、传输线的 SWR 及回波损耗
一个
的负载阻抗接在一条 的传输线上,其长度为 求负载处的反射系数、传输线输入端的反射系数、输入阻抗、传输线的 SWR 及回波损耗。
首先计算归一化负载阻抗,
为图中1️点。利用圆规及圆图下面的电压反射系数标尺,可以读出负载处的反射系数幅值
TRANSM.COEFF, E or I(3),驻波比SWR(4),回波损耗标尺RTN.LOSS[dB](5)。[! note] 在画出等 SWR 圆之后,也可在阻抗匹配点右侧 x 轴与圆的交点出读出 SWR 值。
现在,通过阻抗负载点画一条径向线(2),然后从它与图的外围标尺上的交点读出负载处反射系数的辐角(6)。
现在通过负载阻抗点画一个 SWR 圆。读出负载在朝向波源波长 (WTG) 标尺上的参考位置的值为
(7)。向着波源方向移动 把我们带到 WTG 标尺上的 处(8)。在此位置画一条径向线,它与 SWR 圆的交点给出归一化输入阻抗的值 (9)。于是传输线的输入阻抗为, RC 网络阻抗匹配
阻抗计算
电容阻抗计算式
指向原始笔记的链接 电感阻抗计算式
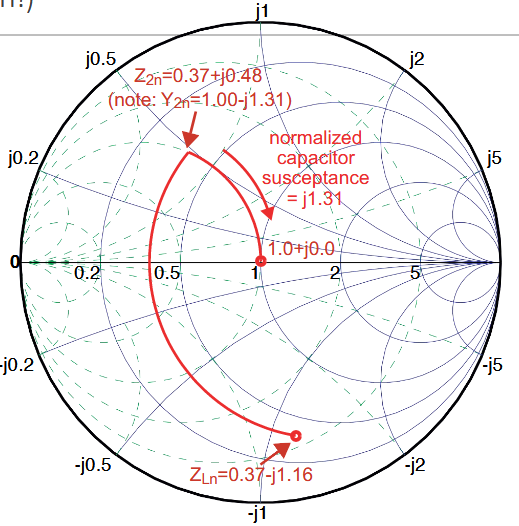
指向原始笔记的链接 计算出负载阻抗之后,将其归一化并标注在史密斯圆图上。
规划移动路线并计算对应的电容电感值
通过串并联电容电感我们能够使得圆图上的点沿着电阻圆或者电导圆顺时针或逆时针移动。通常我们首先将其移动到
或 等于 1 的圆上,然后再移动到匹配点。
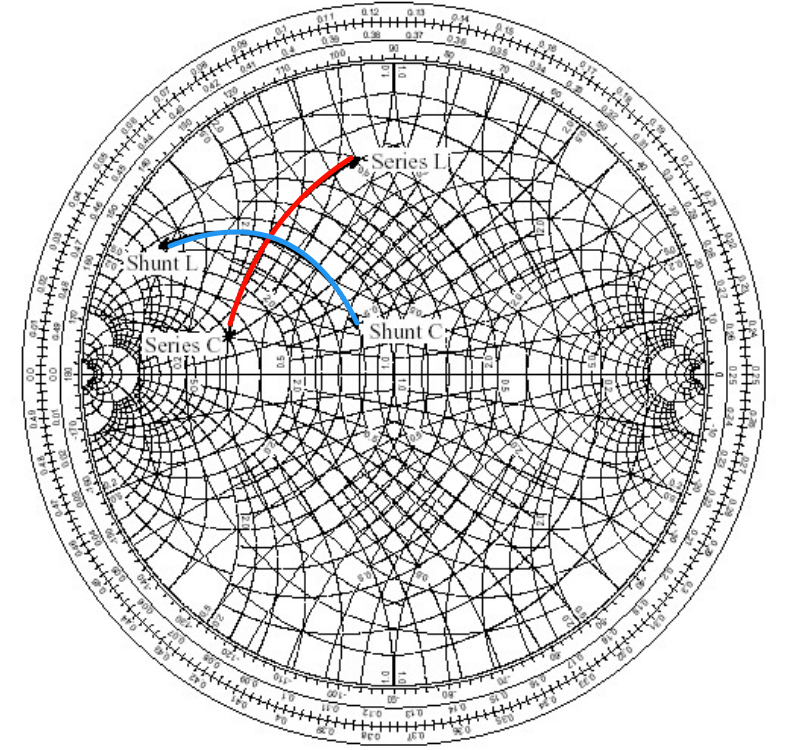
[! tip] 使用 RC 网络进行匹配的时候有以下规律
- 串联电感:正电抗将导致负载沿着等电阻圆顺时针移动;
- 串联电容:负电抗将导致负载沿着等电阻圆逆时针移动;
- 并联电感:负电纳将导致负载沿着等电导圆逆时针移动;
- 并联电容:正电纳将导致负载沿着等电导圆顺时针移动。
简而言之,
- 串联顺着电阻圆移动,并联顺着电导圆移动
- 使用电感就是 Levitate(抬升),使用电容就是Crush(下降)
根据规划的路线进行计算
电容阻抗计算式
指向原始笔记的链接 电感阻抗计算式
指向原始笔记的链接 组合阻抗-导纳的 Smith 圆图
因为绕 Smith 圆图一剧对应于
的长度,所以 的变换等价于在圆图上旋转 ;这也等价于镜像个给定的阻抗(或导纳点)穿过圆图的中心就得到对应的导纳(或阻抗)点。 史密斯圆图含意
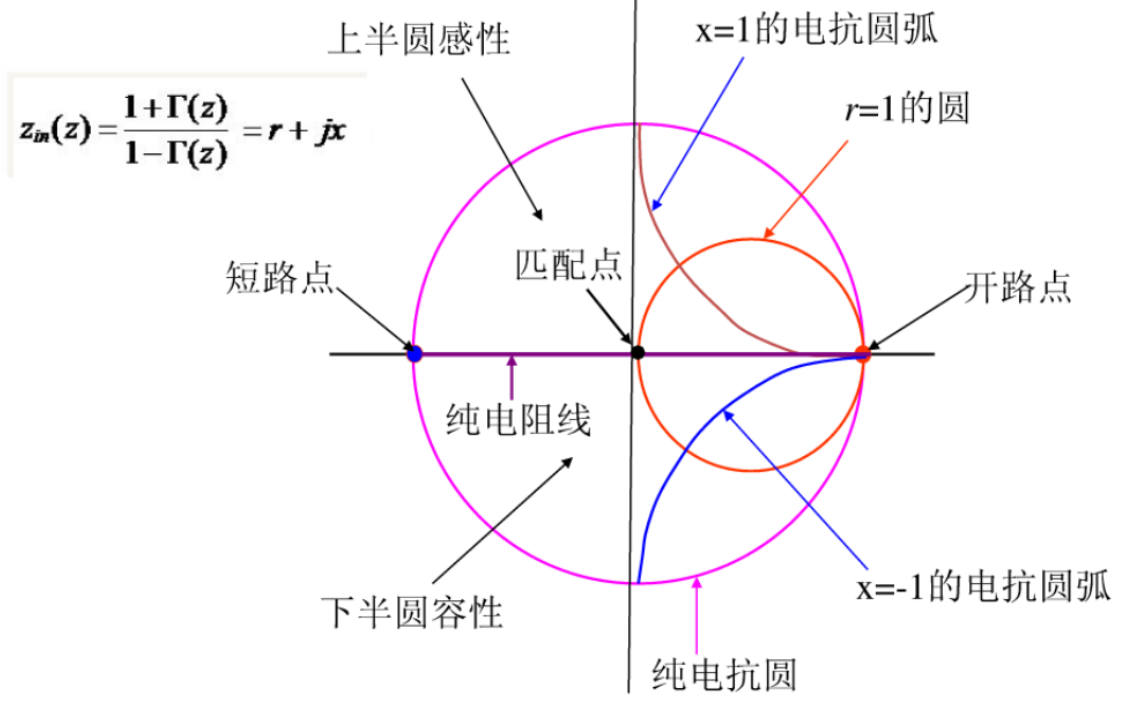
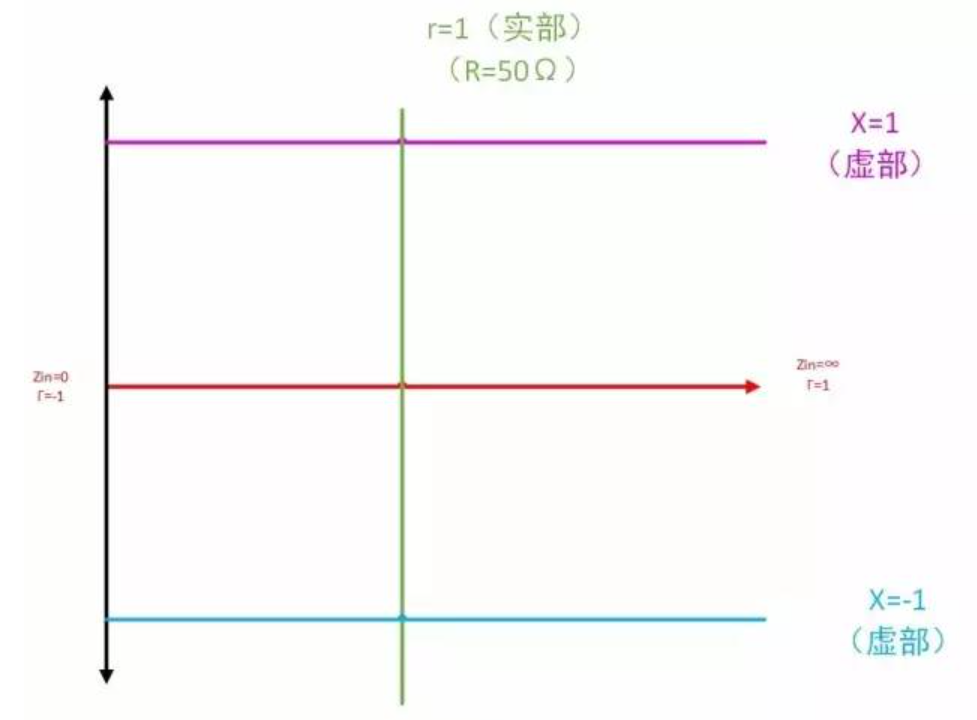
根据上面的推导,可以得出下面的简化圆。
史密斯圆图在作图时,有五条定义线。我们以电阻圆为基础进行讲解。
- 电阻为 0 的黑色线
- 电抗为 0 的红色线
- 电阻为 50
的绿色线 - 电抗为 1 的紫色线
- 电抗为 -1 的蓝色线
画成史密斯圆图的样子如下。
将部分参数标注出来如下。
参考信息
指向原始笔记的链接Info
源和负载失配
共轭匹配
对于固定的源阻抗
即,
满足这个条件的输入阻抗可以使得最大功率传到负载。此时功率为,
有耗传输线
低耗线
如果传输线是低耗的,可以假定
可以得到,传输线复传播常数高频低耗近似
指向原始笔记的链接
传输线传播常数α高频低耗近似
指向原始笔记的链接
传播常数β高频低耗近似
指向原始笔记的链接
采用同级近似,特征阻抗
传输线特征阻抗高频低耗近似
指向原始笔记的链接
.png)