单级微波晶体管放大器工作原理

转换功率增益

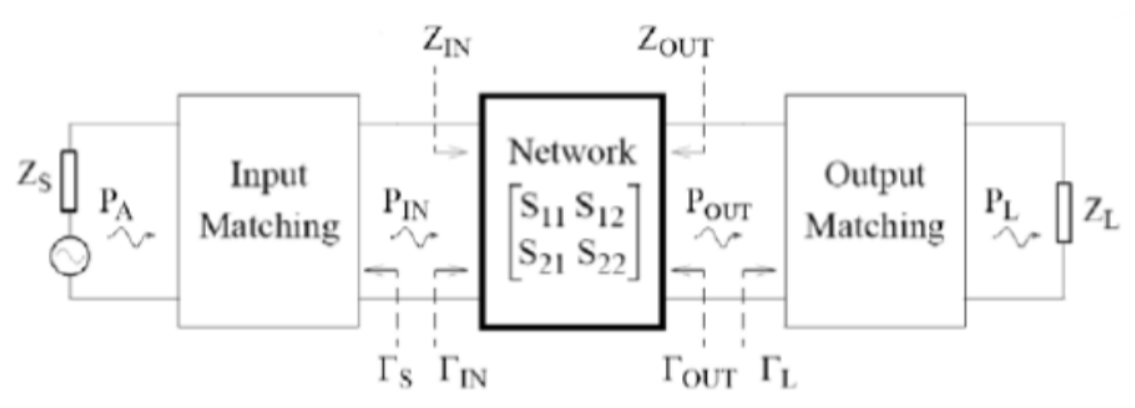
最简单的可以实现的单级放大器由连接到源和负载的单个晶体管组成，源和负载都具有系统特性阻抗 ，我们可以写下 2 端口处的入射功率和反射功率之间的关系网络为：

功率增益的第一个定义是进入端口 1 的功率与从端口 2 发出的功率之比。根据上面的等式，我们可以将其写为：

这就是转换功率增益的计算式。

三种功率增益

实际功率增益

实际功率增益

实际功率增益 是负载 功率与输入到双端口网络的功率 之比。这种增益与源阻抗 无关，尽管有源器件的特性可能依赖于 。

实际功率增益计算式

是负载耗散的功率； 是双端口网络输入功率。

指向原始笔记的链接

实际功率增益只与负载端匹配和放大器的S参数有关，与源端匹配无关。

指向原始笔记的链接

资用功率增益

资用功率增益

资用功率增益 是双端口网络可用功率与源可用功率之比。这假设源和负载都进行了共轭匹配，并且依赖于 ，但不依赖于 。

资用功率增益计算式

是双端口网络的输出功率（资用功率）； 为源的资用功率。

指向原始笔记的链接

资用功率增益与源端匹配、放大器的S参数有关，与负载端的匹配无关。

[! faq] 资用功率增益隐含了负载与输出匹配网络共轭匹配这个条件？ 可以这么理解，因为在负载与输出网络共轭匹配的情况下，

指向原始笔记的链接

转换功率增益

转换功率增益

转换功率增益

是传递到负载的功率与源可用功率之比。

转换功率增益计算式

是负载耗散的功率； 是源资用功率。

指向原始笔记的链接

看向端接网络输出端的反射系数 #挂起/信息不足

转换功率增益与源端匹配、负载端匹配和放大器的S参数都有关系。其是在输入和输出都匹配时发生的一种特殊情况，即零反射 (不同于共轭匹配 ) 的一种特殊情况。这时有 ，

转换功率增益简化计算式

条件：零反射 (不同于共轭匹配 ) ，这时有

指向原始笔记的链接

单边转换功率增益

还有一种特殊情况，就是当 或者小到可以忽略的时候，就能计算单边转换功率增益。

单边增益

这里给出转换功率增益的两种替代表达式，包含输入反射系数或输出反射系数。对于单边设备，其 S12 = 0 (没有从端口 2 到端口 1 的反向传输)，则 且 。转换功率增益的两个表达式都可以简化为以下单边转换功率增益等式

单边转换功率增益计算式

条件：

指向原始笔记的链接

指向原始笔记的链接

单边最大转换功率增益

当器件为单边器件时，并且源和阻抗都共轭匹配了，即 且 ，这时有，

单边最大转换功率增益计算式

条件：，且有 和

指向原始笔记的链接

指向原始笔记的链接

三种功率增益在实际设计中的参考作用

• 在选取放大器时，需要根据设计要求，选用合适的管子，这一般是放大器设计的第一步，这个时候，就需要参考实际功率增益。
• 如果是设计 LNA，除了增益以外，稳定性和噪声也是一个很重要的指标，而对于 LNA 来讲，外接的负载一般是 50 欧姆。所以，LNA 的设计，我觉得输入匹配网络的设计更为重要，因此更多的是参考资用功率增益。但是因为放大器的输出，一般都不是 50 欧姆，输出网络匹配也需要设计，这个设计，更多的是共轭匹配的设计。
• 如果是设计功放，需要输入输出都共轭匹，且输出一般会有一个最佳工作状态 (load pull)，因此这个时候，更多参考的是转换功率增益。

指向原始笔记的链接

端口阻抗失配情况

我们现在考虑任意源和负载终端 和 的更现实情况，它们将具有反射系数 和 ，如下图所示。

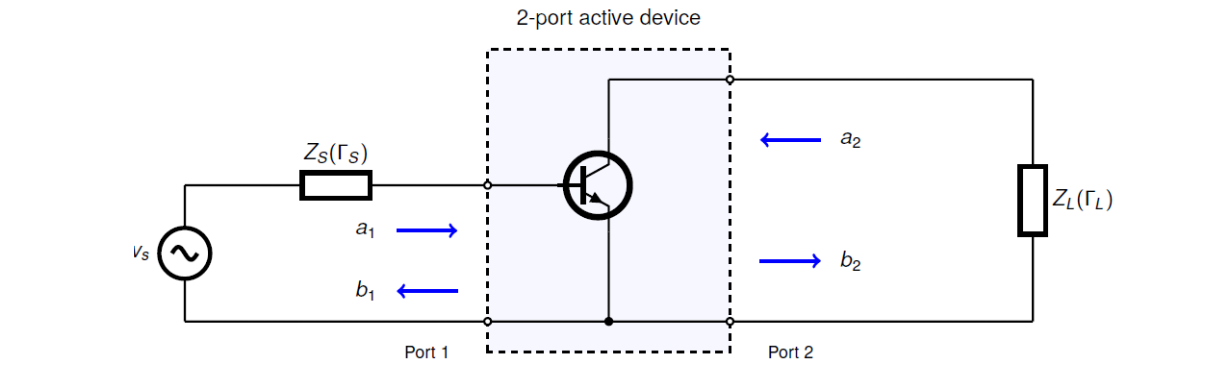
在这种情况下，我们需要修改转换功率增益方程以解决端口处的阻抗失配问题。我们可以写：

其中 和 分别称为源失配因子和负载失配因子。这些「失配系数」表示实际输送到各个负载的功率量占各个电源可用功率的比例（功率在传输过程中被输入阻抗和输出阻抗消耗）：

其中 是来自源的可用功率， 是来自放大器输出端口的可用功率。由于 和 表示在共轭匹配条件下各个源可用的最大功率，因此 和 必须始终 < 1。我们现在分别考虑放大器输入和输出处的功率流，如图 3 所示。

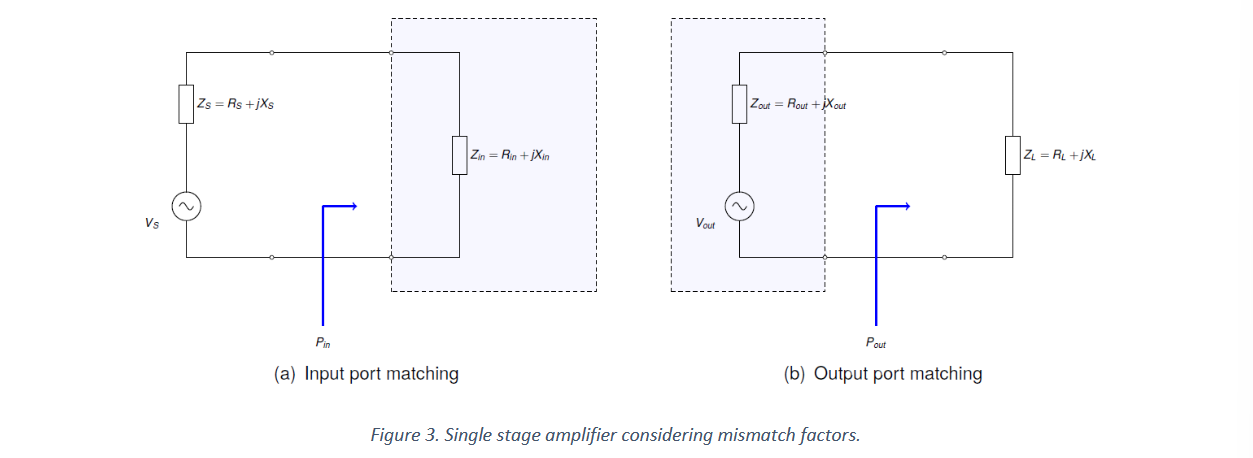
我们首先考虑输入端口。如果我们认为源是共轭匹配的，那么 ，那么源可用的平均功率将是：

注意平均功率是指电流和电压的有效值！ （如果你想知道为什么除以 8 而不是 4）

输送到晶体管输入端的功率为：

然后就能得到，

我们现在可以将上面这个方程转换为仅包含反射系数的形式，

同样，可以得到，

将求 和 的两个方程代入求源失配因子的方程中，就能通过反射系数求得源失配因子，

同样，负载失配因子也有类似的形式，

从上面这个公式我们可以推断，当 时，负载必须与晶体管的输出共轭匹配 ()。计算源失配因子的等式同样表明，当源极与晶体管的输入共轭匹配时， 等于 1。这支持了这样的直观理解：当我们共轭匹配（conjugate matching）输入和输出端口时，将从晶体管获得最大可用增益。此时有 。

然而，对于任何线性双端口，如果存在从端口 2 到端口 1 的反馈（即 S12 > 0），那么输入端口的反射系数 将依赖于负载端，而输出端口的反射系数 将依赖于源端。这被称为非单边双端口。因此，S12 ≠ 0 的晶体管是非单边设备。

而对于非单边晶体管，MS 和 ML 是相互依赖的。这一点很重要，因为它意味着端口不能独立地进行共轭匹配，因为改变 的值会改变 的值，反之亦然。

因此，由于我们只能消除 或 中的一个，所以有两个可能的转换功率增益表达式。

其中，。

其中，。