史密斯圆图是一个用于辅助设计的工具。
史密斯圆图的构成
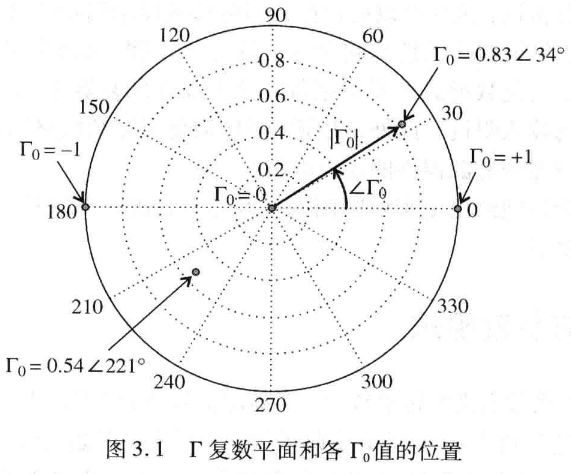
史密斯圆图基本上就是一个电压反射系数
首先,把反射系数用幅值和相位(极角) 的形式表示为
归一化阻抗点
史密斯圆图的真正有用之处是画在图中的阻抗(或导纳)圆,阻抗(或导纳)圆可用来将反射系数转换为归一化阻抗(或导纳),反之亦然。处理图中的阻抗的时,通常用归一化的量。
归一化阻抗计算式
指向原始笔记的链接
为线路的负载阻抗; 为传输线的特征阻抗; 为传输线电阻; 为传输线电抗
根据归一化阻抗即可在史密斯圆图上找到对应的点。归一化阻抗的实数部分对应电阻圆,虚数部分对应电抗圆。
归一化阻抗点与圆心的距离,对应到史密斯圆图的水平标尺 TRANSM.COEFF,E or I 即可找到对应的
也可以根据以下变换公式, 将归一化阻抗转换为复反射系数
归一化阻抗导纳到反射系数的变换公式
指向原始笔记的链接
为归一化阻抗; 为归一化导纳
计算出的
通过这个转换, 可以将复阻抗
.png)
史密斯圆图的应用
史密斯圆图的应用
基本运用
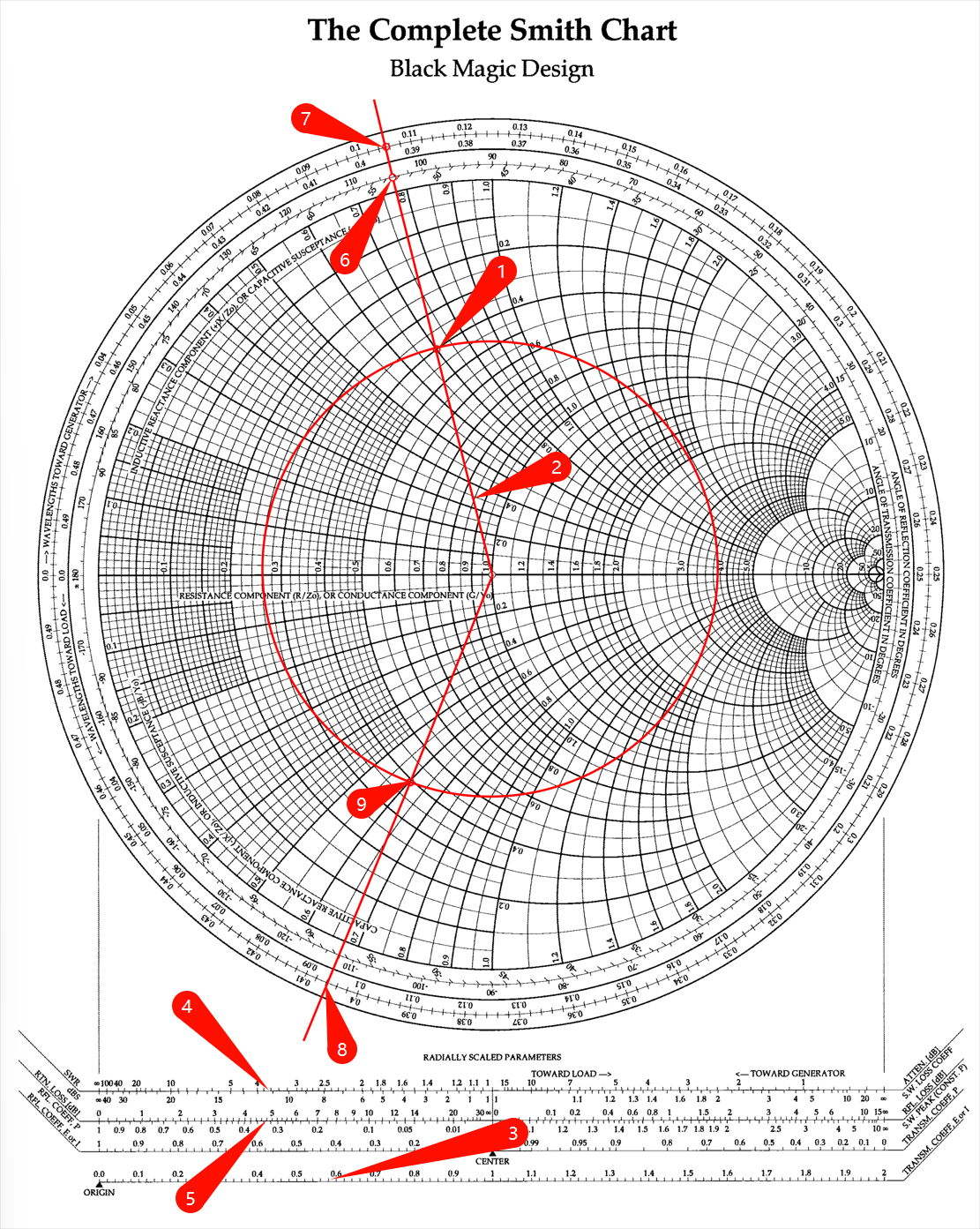
求解负载处的反射系数、传输线输入端的反射系数、输入阻抗、传输线的 SWR 及回波损耗
一个
的负载阻抗接在一条 的传输线上,其长度为 求负载处的反射系数、传输线输入端的反射系数、输入阻抗、传输线的 SWR 及回波损耗。
首先计算归一化负载阻抗,
为图中1️点。利用圆规及圆图下面的电压反射系数标尺,可以读出负载处的反射系数幅值
TRANSM.COEFF, E or I(3),驻波比SWR(4),回波损耗标尺RTN.LOSS[dB](5)。[! note] 在画出等 SWR 圆之后,也可在阻抗匹配点右侧 x 轴与圆的交点出读出 SWR 值。
现在,通过阻抗负载点画一条径向线(2),然后从它与图的外围标尺上的交点读出负载处反射系数的辐角(6)。
现在通过负载阻抗点画一个 SWR 圆。读出负载在朝向波源波长 (WTG) 标尺上的参考位置的值为
(7)。向着波源方向移动 把我们带到 WTG 标尺上的 处(8)。在此位置画一条径向线,它与 SWR 圆的交点给出归一化输入阻抗的值 (9)。于是传输线的输入阻抗为, RC 网络阻抗匹配
阻抗计算
电容阻抗计算式
指向原始笔记的链接 电感阻抗计算式
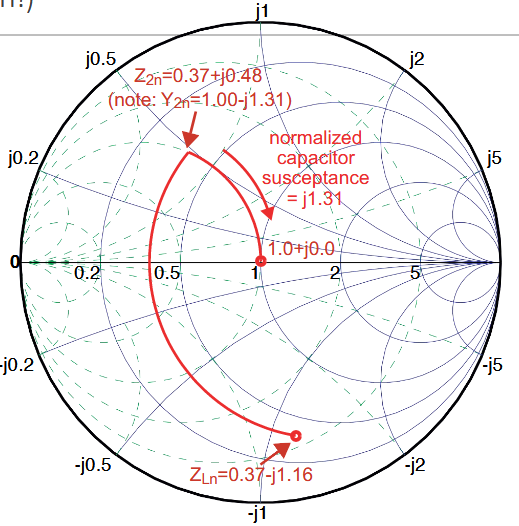
指向原始笔记的链接 计算出负载阻抗之后,将其归一化并标注在史密斯圆图上。
规划移动路线并计算对应的电容电感值
通过串并联电容电感我们能够使得圆图上的点沿着电阻圆或者电导圆顺时针或逆时针移动。通常我们首先将其移动到
或 等于 1 的圆上,然后再移动到匹配点。
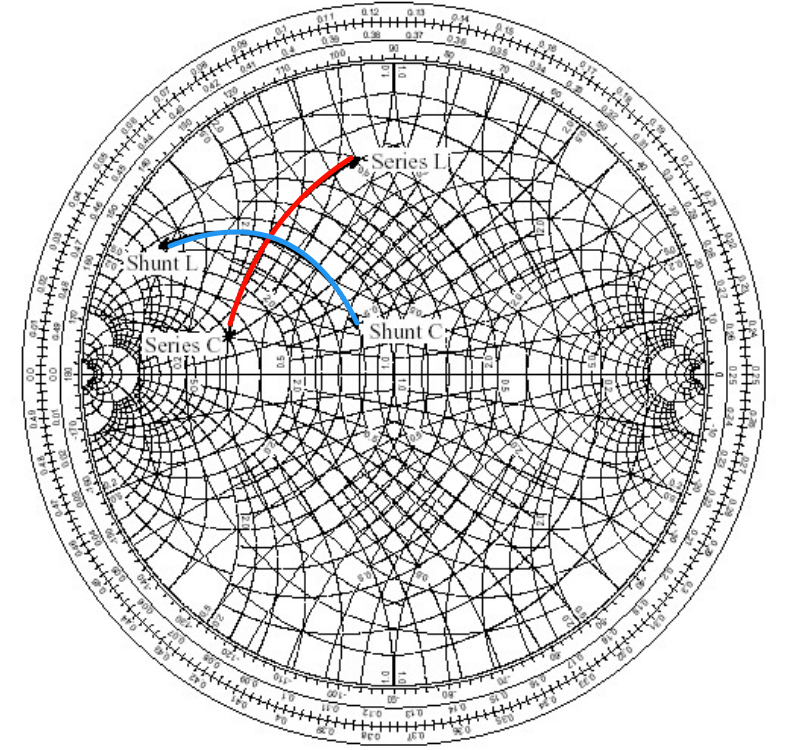
[! tip] 使用 RC 网络进行匹配的时候有以下规律
- 串联电感:正电抗将导致负载沿着等电阻圆顺时针移动;
- 串联电容:负电抗将导致负载沿着等电阻圆逆时针移动;
- 并联电感:负电纳将导致负载沿着等电导圆逆时针移动;
- 并联电容:正电纳将导致负载沿着等电导圆顺时针移动。
简而言之,
- 串联顺着电阻圆移动,并联顺着电导圆移动
- 使用电感就是 Levitate(抬升),使用电容就是Crush(下降)
根据规划的路线进行计算
电容阻抗计算式
指向原始笔记的链接 电感阻抗计算式
指向原始笔记的链接
组合阻抗-导纳的 Smith 圆图
因为绕 Smith 圆图一剧对应于
史密斯圆图含意
根据上面的推导,可以得出下面的简化圆。
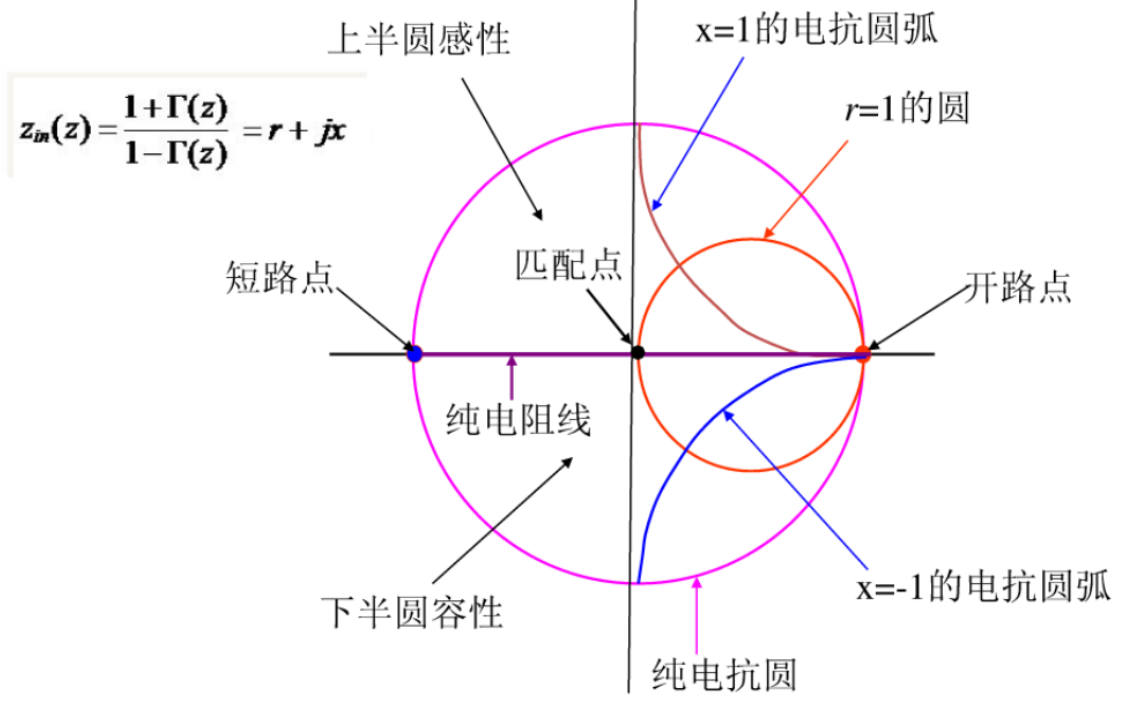
史密斯圆图在作图时,有五条定义线。我们以电阻圆为基础进行讲解。
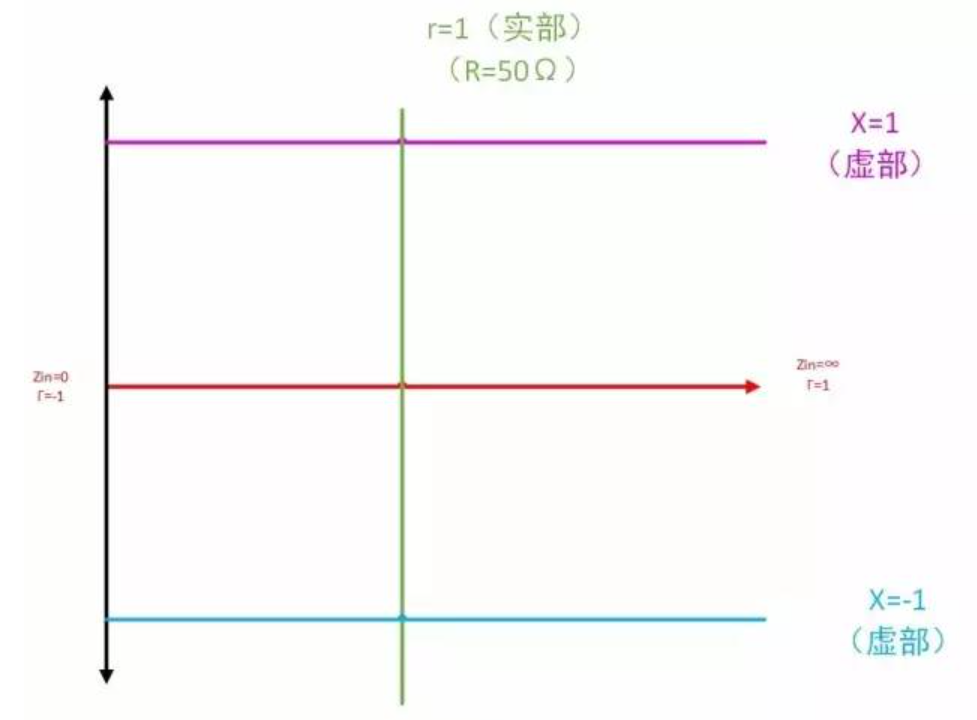
- 电阻为 0 的黑色线
- 电抗为 0 的红色线
- 电阻为 50
- 电抗为 1 的紫色线
- 电抗为 -1 的蓝色线
画成史密斯圆图的样子如下。

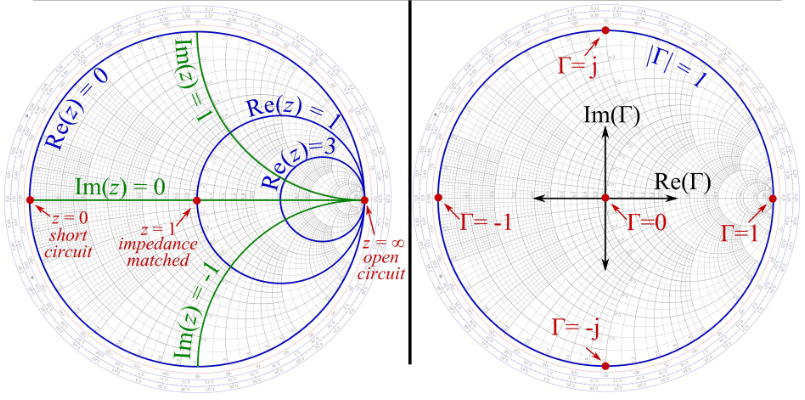
将部分参数标注出来如下。
参考信息
Info