《振荡器》笔记

• 与振荡器相关的基本概念：负电阻的概念
• 基于二端子半导体器件的振荡器的工作原理
• 使用负电阻方法的 RF 晶体管振荡器的设计步骤
• 设计示例

1. 射频振荡器简介

[! reference] “1. Introduction to RF oscillators” (“EE6128RFWC_Slides1 (2024)”, p. 8-13)

[! tldr] 要点总结 这一部分就是射频振荡器定义以及低频振荡器的缺点和一个好的振荡器的标准。这部分了解即可。

射频/微波振荡器是将直流信号转换为稳态射频正弦信号，是微波系统中的基本组件。（一些重要的微波系统）。

微波振荡器是从低频振荡器发展而来，主要的不同存在于晶体管特性，以及实际使用负阻和高 Q 微波谐振器的能力。这里不对低频振荡器做叙述（包括书上的哈特莱电路和考毕兹电路），仅仅介绍其高频应用时的局限性。

振荡器的要求：

1. 优异的频率稳定性
2. 足够的功率输出
3. 低调幅、调相、调频噪声
4. 频率调谐
5. 可调制
6. 电路简单

在其他方面，还会考虑：

• 使用高 Q 值谐振器来提高稳定性的同时降低噪声
• 振荡器推拉能力，即频率随着 dc 偏置电压/负载变化而变化的幅度越小越好，也是稳定性的体现。
• 有源器件需要
  • 具有负电阻： 发电
  • 非线性： 启动振荡并达到稳态

2. 单端口负阻振荡器

Reference

“13.2 微波振荡器” (Pozar, 2019, p. 491)

[! abstruct]

• 理解负电阻的概念
• 振荡器的起振、建立和维持条件
• 能传导最大功率的 的推导

这里我参考的是书上的图。 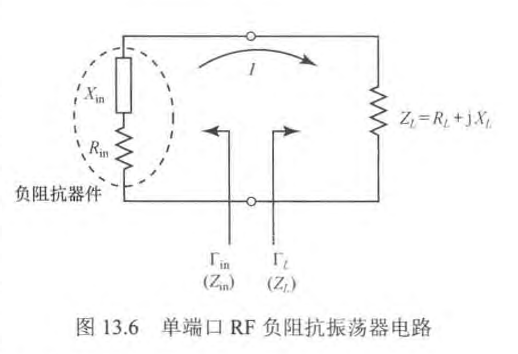上图是一个典型的单端口射频负阻抗振荡器电路，其中 是有源器件（偏置二极管）的输入阻抗，与电流和频率有关；另一边的 是无源负载阻抗。

根据基尔霍夫定律可以有，

根据振荡的定义，如果振荡出现，那么射频电流 不为 0，则需要有条件，

因为负载是无源的， 始终成立，因此这里就可以导出有源器件的输入电阻 是负电阻，也就是一个能量源。而条件二则是控制振荡频率。

对于稳态振荡有 ，可以导出 。并且有 。

[! note] 这里性质总结一下就是，无源负载阻抗的性质照旧，而有源器件的输入阻抗则是反常的，呈现负电阻，反射波幅度大于入射波幅度等性质，也为振荡器埋下伏笔。

[! summary]

• 振荡开始条件：
• 振荡建立条件：环路电阻为负，即 ，此时 不为 0。
• 振荡稳定条件：， 和 为稳定偏置点条件。

2.1. 的选择

单端口振荡器最大功率负载电阻

选择 的实用方法是：选择 的值以获得最大振荡器功率。

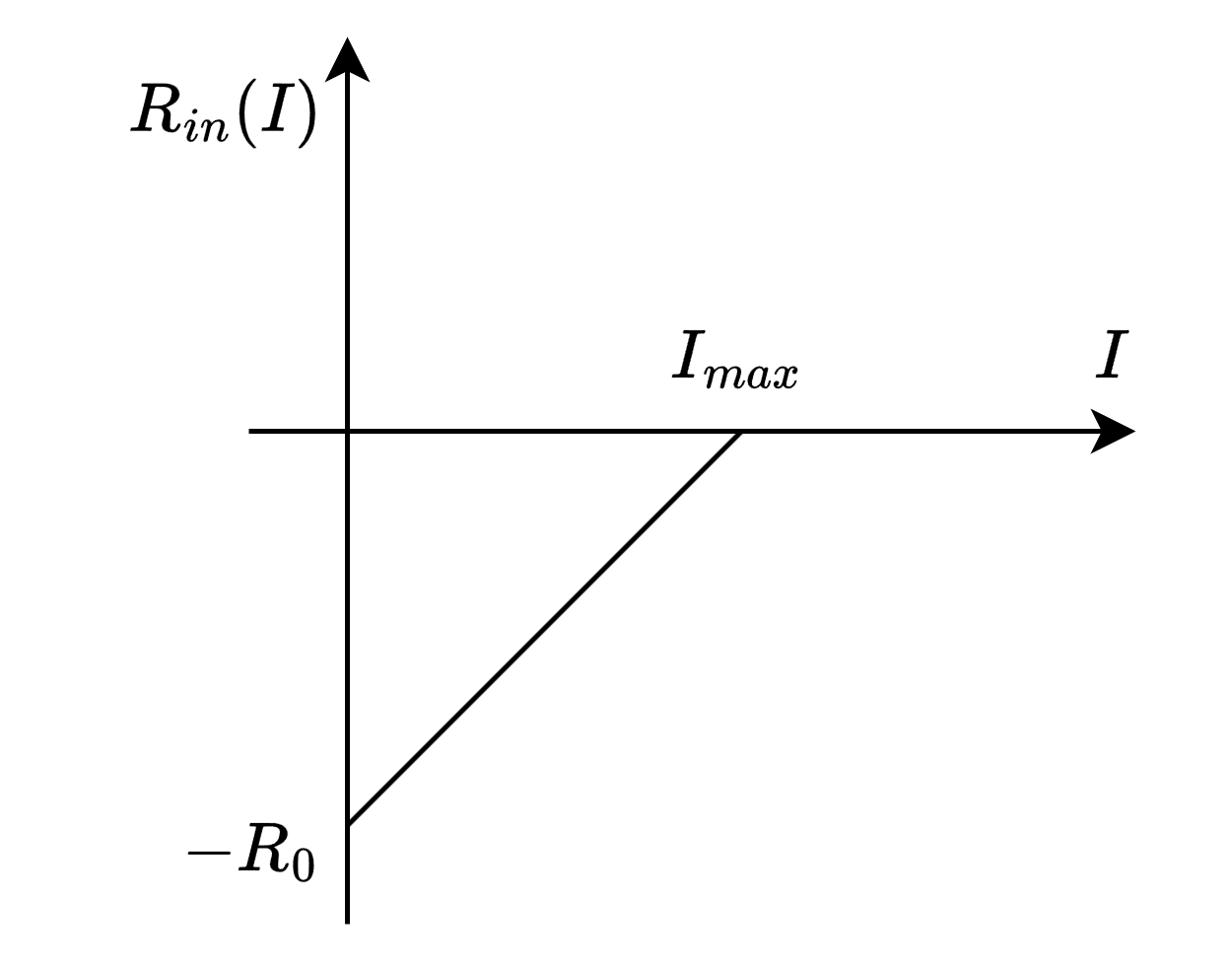假设负电阻 和电流为线性关系，有 。 在这个电路模型中，偏置二极管充当了有源器件，将功率传导给了无源负载电阻 ，于是可以写出公式，

明显可得，当 的时候，功率有最大值，令此时的电流为 ，有输入电阻为 , 则有负载电阻 的时候，能传导最大功率。

3. 二极管

[! reference]

• “11.1.4 其他二极管” (Pozar, 2019, p. 430)（比较粗略）
• “10.2 THE IMPPTA DIODE” (Solid state electronic devices, Streetman和Banerjee, 2015, p. 545)(更详细，看不懂 ppt 或者笔记的可以看这个)

3.1. 耿氏二极管

耿氏二极管使用了特殊的掺杂形式，使得其 I-V 特性曲线呈现负微分电阻。

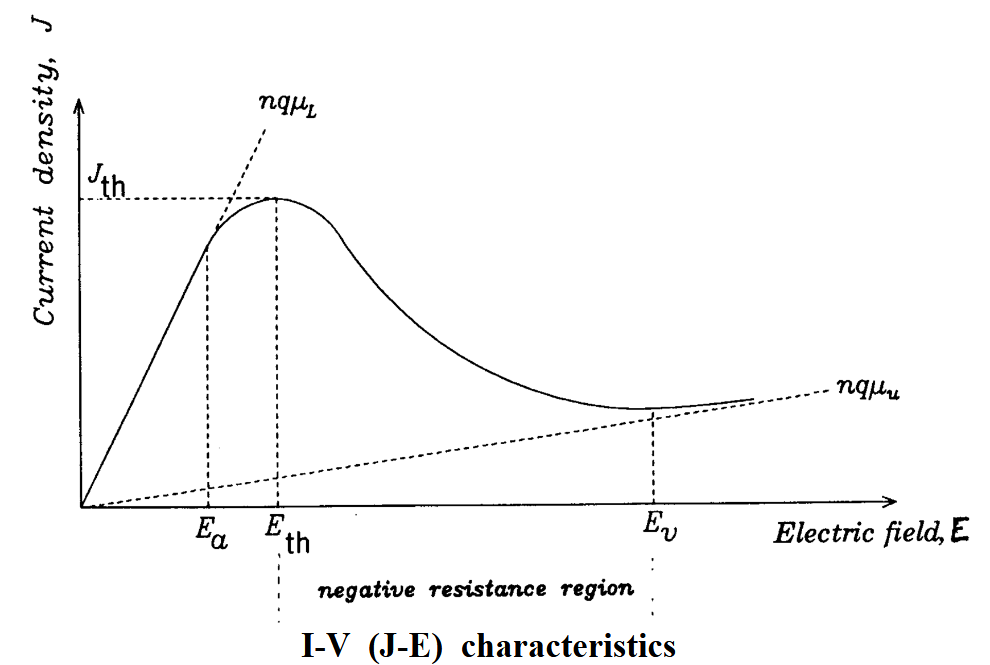
Ridley-Watkins-Hilsun 机制

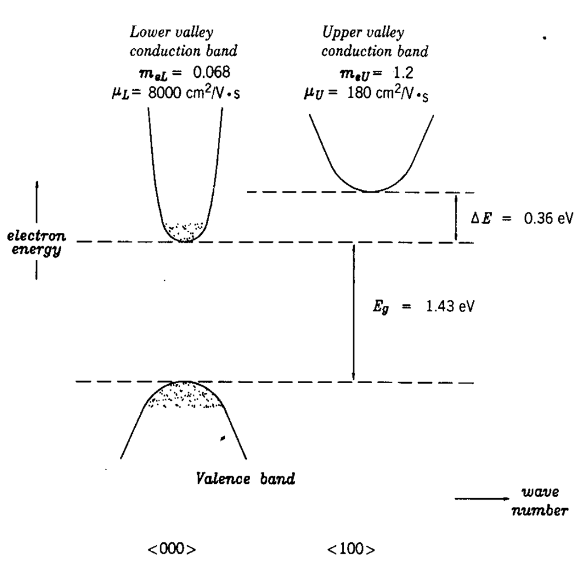
产生负电阻的机制和能带以及迁移率有关。较低的导带底 (中央谷) 具有高迁移率，更小的有效质量和更低的态密度；较高的导带底（卫星谷）具有较低的迁移率，更大的有效质量（中央谷的 8 倍）和更高的状态密度（中央谷的 24 倍）。

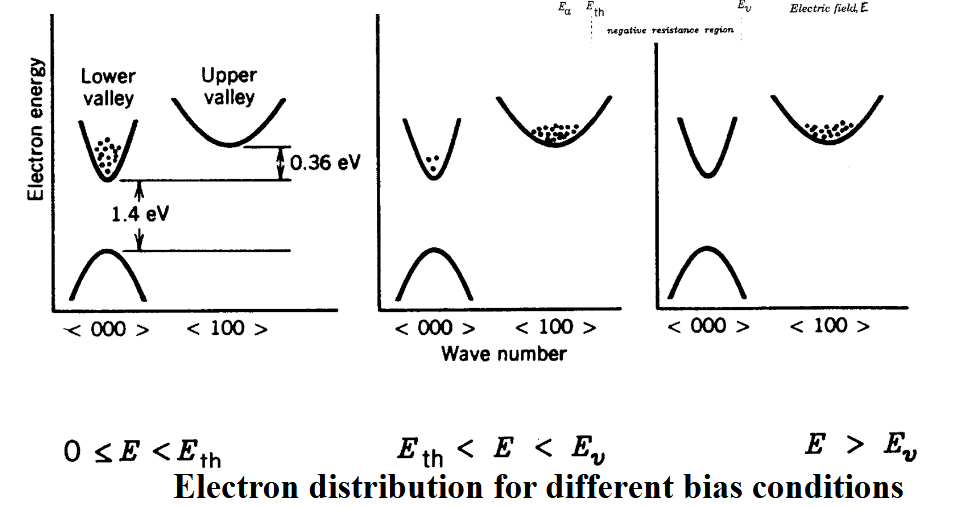
当电压变化的时候，电子从高迁移率的导带底移动到低迁移率的导带底，使得 减小，从而产生了负微分电阻。

能带结构表现出负微分电阻的标准，

1. 。否则，由于热激发，上部山谷将电子稠密。
2. 下谷中的电子必须比上谷中的电子具有更高的迁移率、更小的有效质量和更低的态密度。
3. 。否则，在电子开始从下谷转移到上谷之前，半导体材料就会击穿。

指向原始笔记的链接

耿氏二极管 I-V 特性推导

[! note] 能带结构表现出负微分电阻的标准

1. 卫星谷和中央谷之间的能带差需要大于热电压，否则热激发会导致电子从中央谷跃迁到卫星谷；
2. 卫星谷需要有更低的迁移率、更高的状态密度、更高的有效质量；
3. 带隙需要大于中央谷和卫星谷能带差，否则会发生击穿。

一般的工作模式为双极模式（dipole mode），效率较低。此时，域（电荷区）以饱和漂移速度 （GaAs 为 ）移动到正极。移动时间 ， 为器件长度。

Example 1 耿氏二极管设计*

3.2. IMPATT 二极管和电路

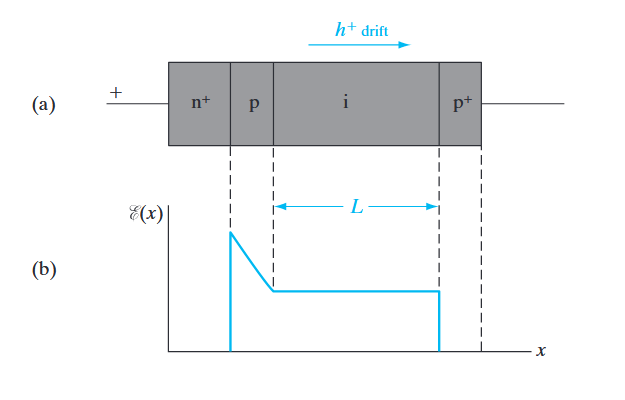IMPATT 电阻可以分为两个区域， 区为雪崩倍增区， 为本征空穴漂移区。也可以用类似的 结构，那么雪崩倍增产生的就是电子。

IMPATT 二极管是利用雪崩击穿和载流子渡越时间效应的二极管。负电导的发生是由于两个过程，导致电流在时间上滞后于电压：(1) 由于雪崩过程引起的延迟；(2) 由于载流子穿过漂移区的渡越时间引起的进一步延迟。如果这些延迟时间之和约为工作频率的二分之一周期，则出现负电导，器件可用于振荡和放大。

雪崩区具有较薄、高掺杂的特点，用于产生高电场。漂移区则是长且轻掺杂，用于延长渡越时间产生延迟。

其中 α 是电离率； m、b 和 A 是常数。

4. BJT 特性

这里比较一下 BJT 和 或者 BJT. HBT 在高频增益更高，噪声也更小。

5. 场效应晶体管特性

材料和形式:

• GaAs（砷化镓）
• MESFET（金属半导体场效应晶体管）
• 肖特基势垒栅

特性

• 高电子迁移率：可实现出色的频率响应和噪声性能，尤其是在 6 GHz 以上

应用

• 6 GHz 以下：极低噪声应用
• 6 GHz 以上：首选晶体管

6. 晶体管的 S 参数

大概率不会考，应该是仅仅作为知识补充吧。

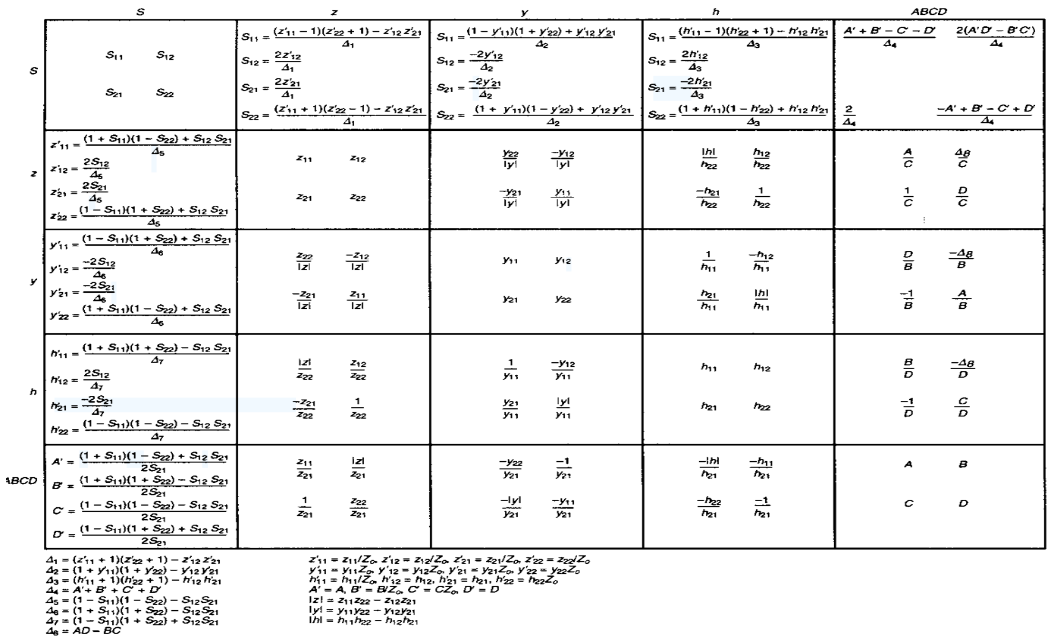
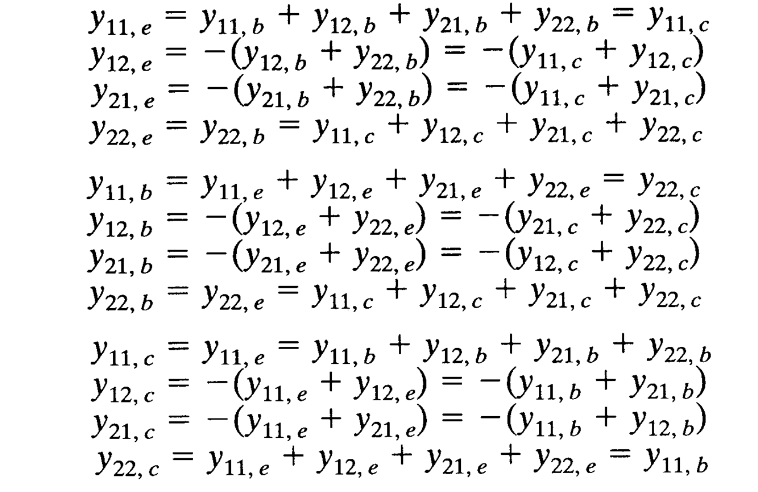
7. 振荡条件

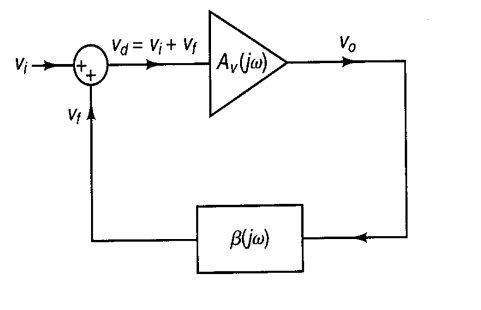
巴克豪森准则

对于一个用带有频率相关反馈路径的放大器电路，当输入电压为 0 而输出电压不为 0 的时候，形成振荡器。即为闭环增益为 1 （unity）的时候。

我们定义有 为开环增益（open-loop gain）， 为闭环增益（close-loop gain）。根据巴克豪森准则，有 。 和 都应该是复数，但是我们考虑在在中频区域的增益为一个常实数。于是有，

这里说明的实际上就是在形成振荡器的时候，传递函数的条件。

指向原始笔记的链接

对于信号流图不熟的先看看这篇笔记，然后我们就能分析这个信号流图了。 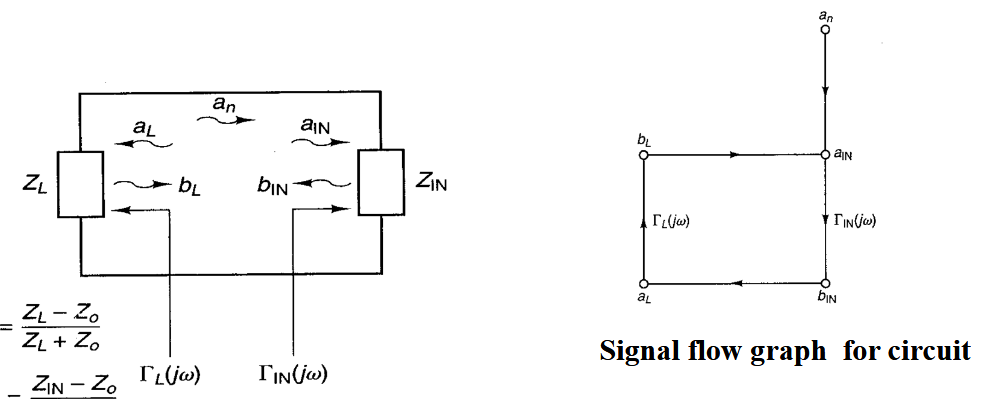像这里没有标注系数的支路，相当于节点可以直接合并，。负载阻抗的入射波为，

对于振荡器，环路增益需要为 1，于是有，

8. 2 端口负阻振荡器

[! reference] “13.2.1 晶体管振荡器” (Pozar, 2019, p. 492)

2 端口负阻振荡器的构建方法是，在二极管的终端端口接上合适的终端负载，从而建立一个负阻抗的单端网络。

晶体管的任一端口都可以用作终端端口, 另一个端口称为输入端口。负载网络连接到输入端口，与单端口表示法一致。

终端阻抗需要使得器件能在不稳定区域内驱动。

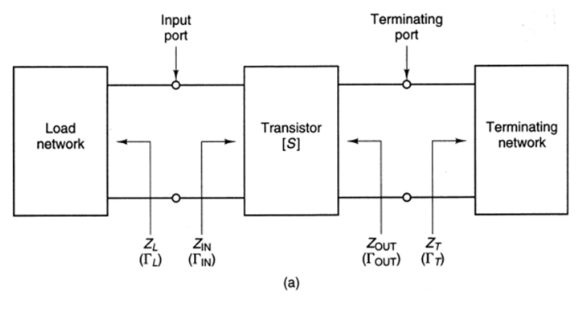
稳定振荡的条件和单端口负阻振荡器一样， 的选择也是一样参考这一节的内容，不再赘述。

8.1. 终端端口的振荡

当输入端口在振荡的时候，终端端口实际上也在振荡。下面来证明这一点。

首先画出输入反射系数的信号流图。终端网络被处理成了 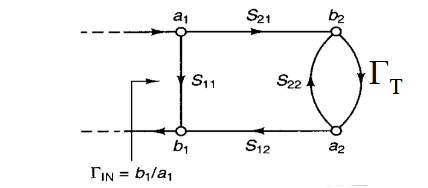连接二极管的输出端口的入射波和反射波。 由前面的的关于稳定振荡时的推导，当输入端口稳定振荡的时候，有 。通过信号流图能推出，

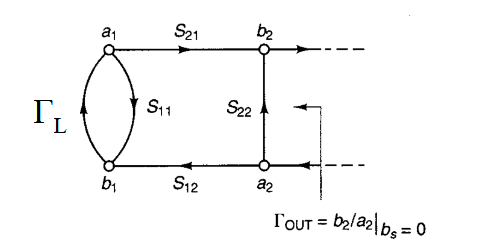随后来推导输出反射系数，同样能得，

可以看出，

于是就能得出终端网络端口也在振荡。

[! note] 这里就能看出来，、、、 都是相互联系的。

8.2. 振荡器设计流程图

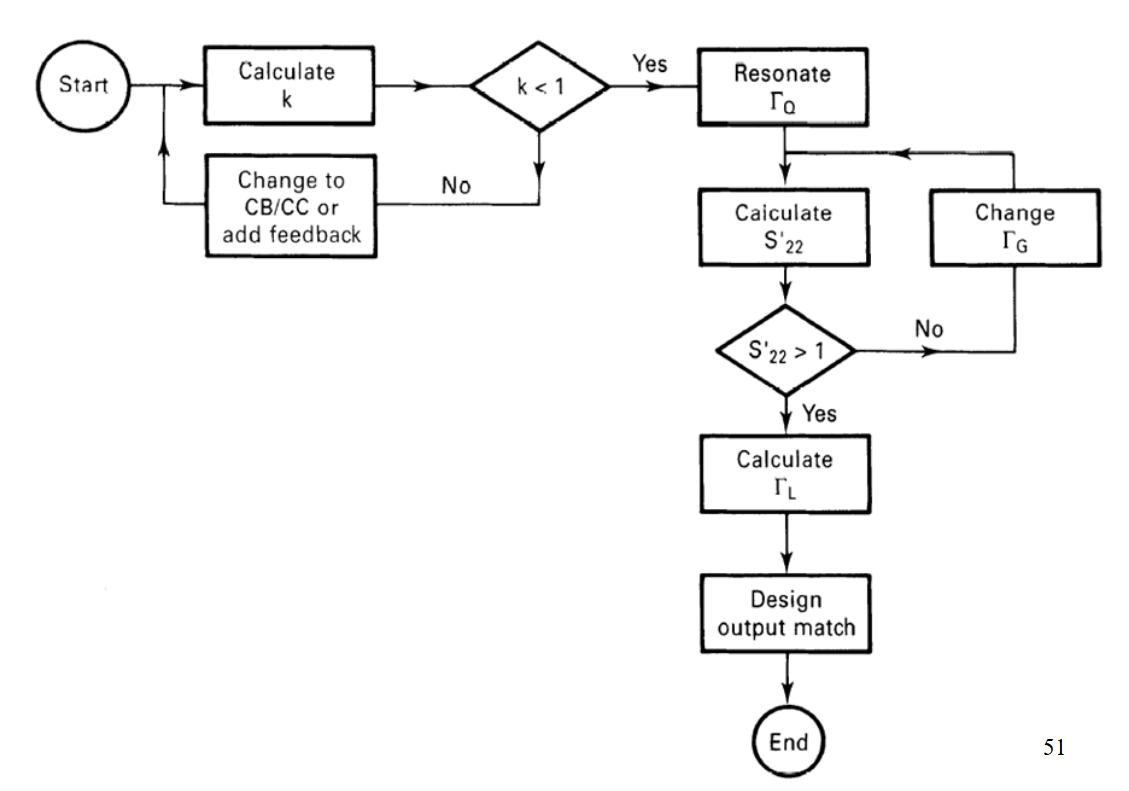
这里直接看例题会更好。

Example 2 FET 振荡器的设计

Example 3 BJT 振荡器的设计

9. 大信号设计方法

10. 使用谐振电路的稳定振荡器

11. LC 振荡器拓扑

12. 微波振荡器拓扑

13. 介质谐振振荡器

介质谐振振荡器在微波频率下有高 Q 且温度稳定的特性。例如在 8 GHz 时，能实现在 -50°C 至 80°C 范围内 500 ppm 的频率稳定性，频率漂移 = 4 MHz。

介质谐振器工作于 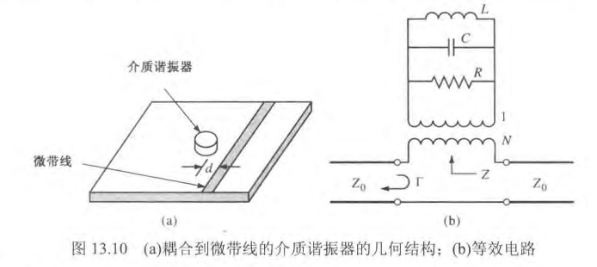模，并且放置于微带线旁，通过磁场与其进行耦合。耦合强度与器件间距离 有关。由于是通过磁场耦合，介质谐振器表现为串联负载，于是有等效电路， 谐振器建模为 RLC 并联电路 ,与馈线的耦合建模为变压器的圈数比 N。微带线看到的等效串联阻抗 为，

有无载谐振器 Q 值 ，谐振频率 ，。

再定义谐振器和馈线之间的耦合系数，为无载 Q 值和外 Q 值的比，

example 4 DRO 的设计

14. 压控振荡器