1. 测试
测试面临的问题是,如何用最少的测试模式去获得最高的故障覆盖率。
测试流程
- 要测试哪些故障?(故障建模)
- 如何获得测试模式?(测试模式生成)
- 如何测量测试质量 (故障覆盖率)?(故障仿真)
- 如何应用测试向量和评估结果?(ATE/BIST)
1.1. 缺陷 Defect
电子系统中的缺陷是指硬件上的瑕疵,缺陷类别有:
- 随机缺陷,独立于设计和工艺;
- 系统性缺陷,取决于用于制造的设计和工艺。
系统缺陷可能是由工艺变化、信号完整性和设计完整性问题引起的。随机缺陷和系统缺陷可能同时发生在单个芯片上。随着特征尺寸的不断缩小,低于 180nm 技术节点,系统缺陷对良率的影响比随机缺陷更大。
故障是缺陷的一种代表, 用于计算机程序中分析电子组件的缺陷。
2. 故障模型
I/O 功能测试不足以满足制造需求 (功能测试与组件及互连测试的对比) 。真实缺陷 (通常为机械性) 数量过多且往往无法分析。故障模型确定了测试的目标,使分析成为可能,并且通过实验可衡量其有效性。
2.1. 按故障性质分类
- 逻辑故障 。一个导致电路元件的逻辑功能更改为其他功能;
- 参数性故障。指改变电路参数大小, 导致电阻、电容、电流等因素发生变化的故障。
- 延迟故障。一种与电路延迟相关的问题, 如门电路速度慢, 通常会影响电路的时序, 可能导致冒险或性能下降等情况。
2.2. 按故障持续时间分类
- 永久性故障。一种持续且稳定的持久性故障, 其性质在测试前、测试中和测试后均不发生变化。例如, 断线、错误的焊接等。亦称硬故障或固定故障;
- 临时故障。一种仅间歇性出现的故障, 它在随机时刻发生, 并在有限但未知的时间段内影响系统。
- 转换故障由环境条件引起, 例如宇宙射线、 α 粒子等。在 RAM 中也被称为软错误;
- 间歇性故障由非环境条件引起, 例如组件参数的边际值、磨损或关键时序;
2.3. 故障建模
众所周知,集成电路是有不同的抽象层次的。故障建模的目的是将物理缺陷(如制造缺陷、信号完整性等问题)抽象为更高设计层次的可测试模型,以便生成有效的测试模式。这个过程涉及从晶体管级到逻辑门级,再到 RTL级甚至系统级的抽象,不同层级对故障的表示和覆盖能力不同。
抽象层级越高,故障数量越少,同时能仿真的底层故障越多。但是高层级的测试也可能遗漏底层故障。
所以一个好的验证策略就是自顶向下,先针对高层的故障模型生成测试,确定测试覆盖的范围之后,再去用测试覆盖没有测试到的故障。
[! important] 后面的所有故障模型都是结构故障模型,即假设硬件模块没有故障,仅组件的互联可能存在故障。
2.4. SSA 故障✨
SSA(single Stuck-At),单线固定故障,指给定线路具有恒定值 ( 0/1 ), 与电路中其他信号值无关。
2.4.1. SSA 故障的数量
在数字电路测试中,故障点(Fault Site) 是指电路中可能发生逻辑故障的物理或逻辑位置。对于一个布尔门级电路(Boolean gate-level circuit),故障点的总数通常由以下三部分组成:
其中:
:电路的原始输入(Primary Inputs)数量。。 :电路中的逻辑门(Gates)数量。 :电路中所有扇出分支(Fanout Branches)的总数。
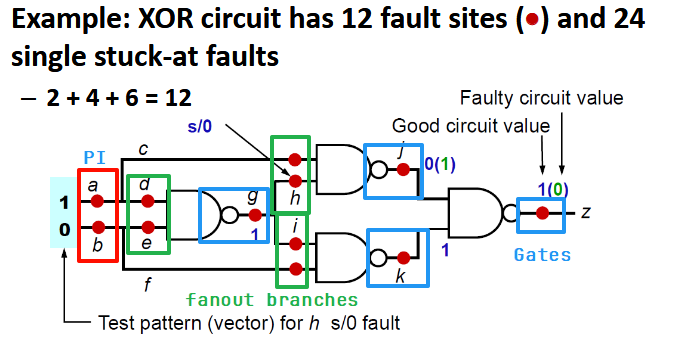
然后每个故障点能发生 SSA0 或者 SSA1 两种错误,所以有 24 个 SSA 错误。
[! tip] 除了门级电路的标准门之外,输入、输出和扇出也被定义为了组件。
2.5. MSA 故障
多重固定型故障(Multi Stuck-At )指多个单固定型故障同时发生。实践中通常不考虑多重固定型故障, 原因有二:
- 在含有 k 个节点的电路中, 多重固定型故障的数量线数为
, 即使对于中等规模的电路来说, 这个数字也太大了; - 当电路规模较大且具有多个输出时,针对单固定型故障的测试已知能覆盖很大高比例 (大于 99.6% ) 的多重固定型故障;
2.6. 开关级故障模型
开关级故障模型描述的是开关级电路描述中的晶体管故障。这种故障模型主要用于 MOS 技术,特别是 CMOS 技术。此类别中最突出的是 stuck-open 和 stuck-on 故障模型。
2.6.1. 固定开路故障模型 Stuck-open fault( SOpF )
晶体管因某些缺陷永久性不导通。
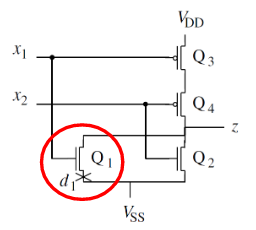
假设有个序列:
SOpF 测试需要一个向量序列。
2.6.2. 固定导通故障模型 Stuck-on fault model SOnF
晶体管因某些缺陷而永久导通。
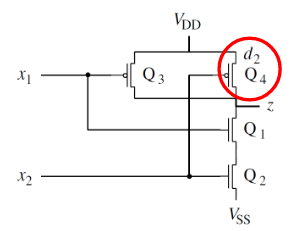
缺陷 d2 导致门始终导通:Q4 中的 SOnF。唯一应用于 NAND 门的向量是 (1, 1; 0)。在故障存在的情况下, 晶体管 Q1 、 Q2 和 Q4 将导通, 导致输出端出现某个中间电压。
监控故障的方法:
- 逻辑监控:输出逻辑值,快速;
- 电流监控:SOnFs,慢速;
2.6.2.1. 用
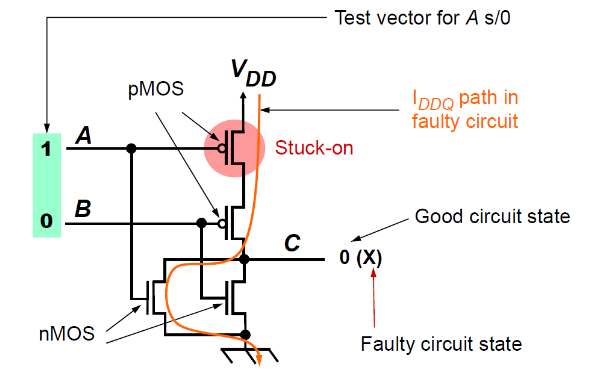
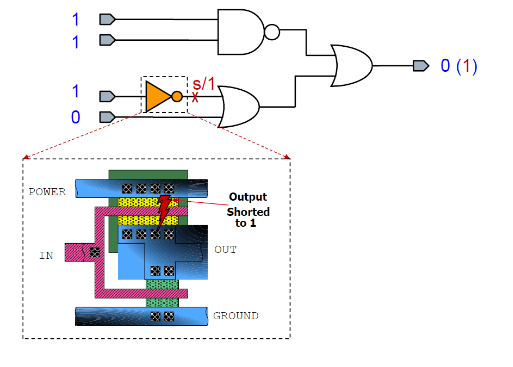
用 CMOS 电路在稳定状态时,从电源到地的直流电流对故障进行测试。如示例所示,A 给 1 信号,B 给 0 信号,正常来说应该输出 0;如果输出
但是在纳米时代,
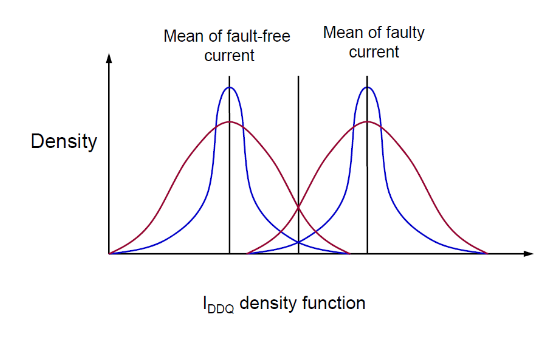
- 若正常芯片的尾部与故障芯片的头部重叠(如图中交叉部分),会导致:
- 误判(False Positive):正常芯片因电流偏高被误判为故障 → 良率损失。
- 漏检(False Negative):轻微故障芯片被误判为正常 → 可靠性风险。
2.7. 几何故障模型 Geometric Fault Model
直接源自电路布局。利用线宽、线间距离、组件间距以及器件几何形状的知识, 来确定最可能出现的缺陷。
桥接故障 (BF):最有可能导致短路的缺陷;
- 与桥接故障:两条线桥接产生 AND 功能;
- 或桥接故障:两条线桥接产生 OR 功能;
2.7.1. 桥接故障 Bridging Faults
桥接故障:两个或多个通常独立的点 (线) 被短路连接在一起。一般有两类:
- 输入桥接:可形成有线逻辑或投票模型
- 反馈桥接:可能引入反馈,导致振荡或者锁存。
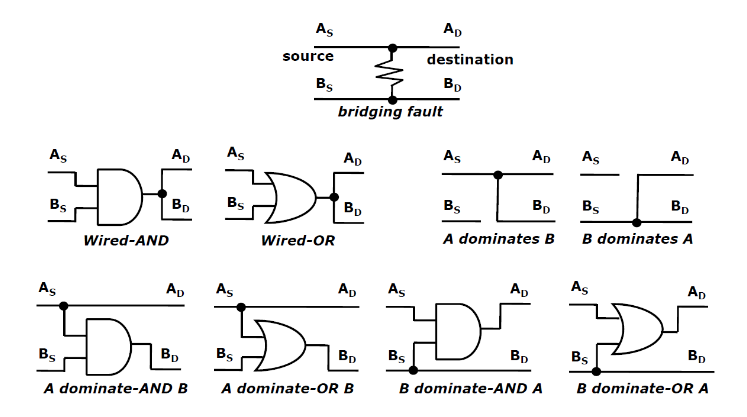
可以看到分三类:线与/或;支配;支配与/或。
2.7.2. 模式敏感故障 Pattern-Sensitive Faults
模式敏感故障(教材中叫状态依赖型故障),故障信号的存在取决于邻近点的信号值。在 DRAM (动态随机存取存储器) 中最为常见。
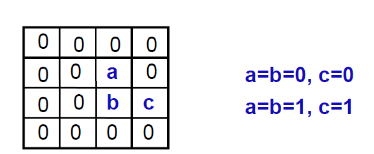
耦合故障,一对单元之间的模式敏感性。
2.7.3. 单元故障 Single Cell Fault
单元故障指的是数字电路中一个基本逻辑单元(如与门、或门、非门、多路复用器等)内部出现的故障。这些单元在电路中通过例化的方式被多次使用,单元故障表现为该单元的真值表(即输入到输出的映射关系)被任意改变; 真值表可以以任何方式改变。
单元可测试性:恒定数量的测试模式,与电路大小无关(纹波进位加法器对所有单固定故障仅需 8 个测试模式)。
2.7.4. 延迟故障模型 Delay Fault
故障可能仅影响电路的时序行为, 而非其逻辑行为。其分类如下:
- 门延迟故障 (GDF): 门的输入或输出具有表现为缓慢 0 → 1 或 1 → 0 转换。
- 集总门延迟故障 (G‐GDF): 延迟缺陷超过 > 时钟周期, 是灾难性故障;
- 小门延迟故障 (S‐GDF): 延迟缺陷小于 < 时钟周期, 至少一条路径出现时序故障, 需对每条路径进行两次测试以检测。
- 路径延迟故障 (PDF): 存在一条路径, 该路径在传播 0 → 1 或 1 → 0 转变时较为缓慢。
2.7.4.1. 延迟故障测试
- 无冒险健壮性测试 (HFRT):无论门限延迟值如何,确保测试路径上都不会发生冒险;
- 非无冒险健壮性测试:允许沿测试路径存在冒险;
- 多路径传播 (MPP):测试通过多条路径将转换传播到输出;
- 单路径传播 (SPP):转换传播通过单路径完成;
- 单输入更改 (SIC): 从初始化向量到测试向量,只有一个输入发生变化;
- 多输入变化 (MIC):从初始化向量到测试向量,多个输入发生变化;
2.7.4.2. 转换延迟故障
转换延迟故障,一个门的输出可能上升缓慢或下降缓慢, 并且这个时间超过预设水平。若延迟故障足够大, 过渡延迟故障将表现为 SAF, 并可采用该方法建模
过渡延迟故障的主要弱点:
- 需要两个模式序列用于初始化和过渡检测
- 由于时序冒险的存在, 最小可实现的延迟故障大小难以确定。因此, 通常使用整个任务时钟周期
2.7.5. 串扰故障
由于线宽缩放导致产生了两个信号网络之间的寄生耦合,从而导致电容性串扰。
2.7.5.1. 最大攻击者模型
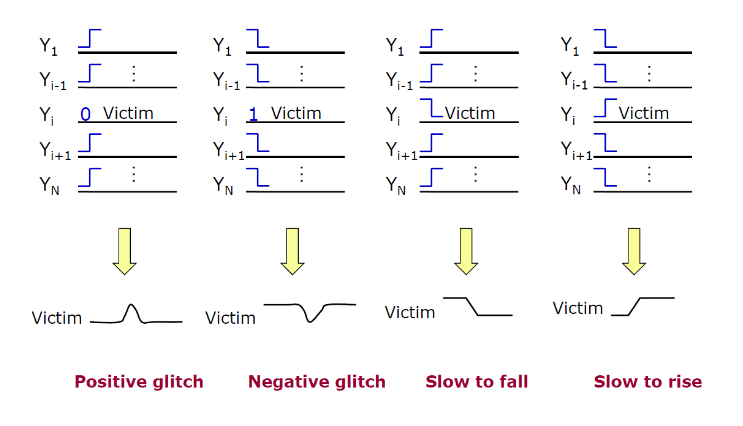
3. 测试、测试向量✨
[! note] 这一节关于“测试”的定义 故障电路产生的输出异于正常电路的输出, 其输入端的一组值叫作针对该故障电路故障的一次测试。
对电路 C 中的故障 进行测试, 就是为其提供一个输入组合,当 存在时, C 的输出与 a不存在时不同。
- 也称作测试模式或者测试向量;
检测到 ,则有
针对一类故障
故障
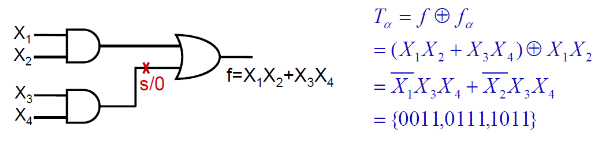
这里
3.1. 测试与诊断
测试是一个包含测试模式生成、测试模式应用和输出评估的过程。
- 故障检测用于判断电路是否存在故障;
- 故障定位提供检测到的故障位置;
- 故障诊断提供检测到的故障位置及类型。
4. 故障压缩✨
为数字电路生成测试时, 测试工具会接收电路描述 (即网表)。随后, 工具会创建一份待检测故障的清单 (故障列表) 。对于大型电路, 列表可能会相当冗长。因此, 尽可能缩短列表是有益的。
某些故障可能会被相同的测试模式检测到。因此, 故障列表中只需包含这些故障中的一个即可。故障压缩能够通过两个概念来缩减故障列表的规模: 等效 equivalence 与支配 dominance。
4.1. 等效故障压缩
如果每一个能检测出一个故障的模式也能检测出另一个故障, 则称这两个故障是等效的。
总结:
- 与门:所有 s/0 故障等效;
- 或门:所有 s/1 故障等效;
- 对于一个
输入的门电路,通过等效故障压缩,仅需要考虑 个故障。
4.1.1. 通过故障图压缩
用一对圆表示每条线 x: 上方的圆代表 x/1, 下方的圆代表 x/0。也就是说每个点代表这个接口可能出现的错误(我们这里只分析 SSA)。
拿与门进行分析。如果其某个输入 SA0,那么其输出也必然表现出 SA0,然后与这个门的输出相连的逻辑也被这个 SA0 影响,从而表现得与输入的 SA0 没有区别。
这意味着与门三个端口上的 SA0 形成一个等价类,类构件之间无法区分。我们就用一条无向的线将等价类连接起来,它们在所有可能的输入测试模式下,对电路输出的影响完全相同。
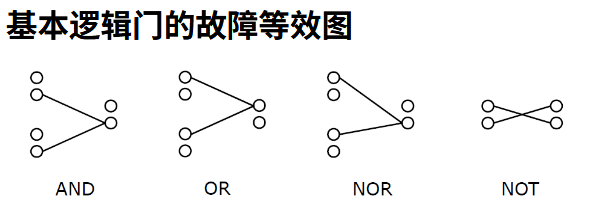
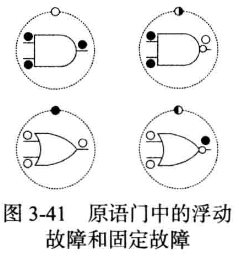
[! question] 与教材描述不同 教材这里还提到了一种浮动故障:“一个 n 输入 NOR 门在其输入上有 n 个固定 SAO 故障, 在输出上有 1 个固定 SAl 故障, 以及 1 个浮动故障 (若置于输入上则会以 SAl 的面貌出现, 若置于门的输出上则会变为 SAO)。”
但是这里没讲就先暂时不考虑。
4.2. 支配故障压缩
一个故障
总结:
- 对于一个 n 输入与门,输出故障
支配了输入故障 ; - 对于一个 n 输入或门,输出故障
支配了输入故障 。
4.2.1. 通过故障图压缩
从支配故障向被支配故障添加有向线。支配故障等效于被支配故障,也就是说,检出了被支配故障等同于检出了支配故障,但是检出了支配故障不等于检出了被支配故障。
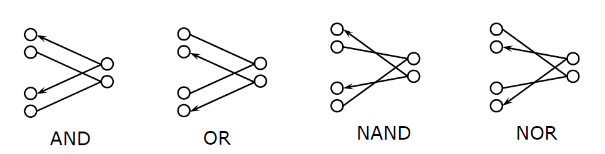
对于扇出结构, 将主干和分支视为独立的线路。支配方向与门电路相反。

4.3. 计算故障压缩后所需测试的数量。
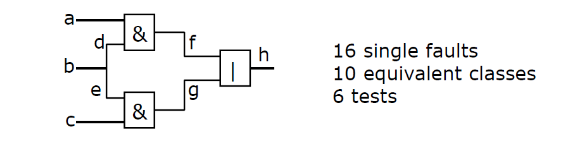
给出电路如上。再说明等效压缩和支配压缩在应用上的实际含意。
- 等效压缩,说明测试其中一个故障,等于所有等效的故障都测试了;
- 支配压缩,说明只要测试被支配的故障,支配故障就相当于被测试了。
所以根据前面所说的与门和或门的等效压缩和支配压缩画出图。下图是其中一种等效故障的画法。只要是等效的,你就可以连在一起;但是被支配的故障之间是无法通过一次测试覆盖,所以要分两个测试。红点就是测试点。
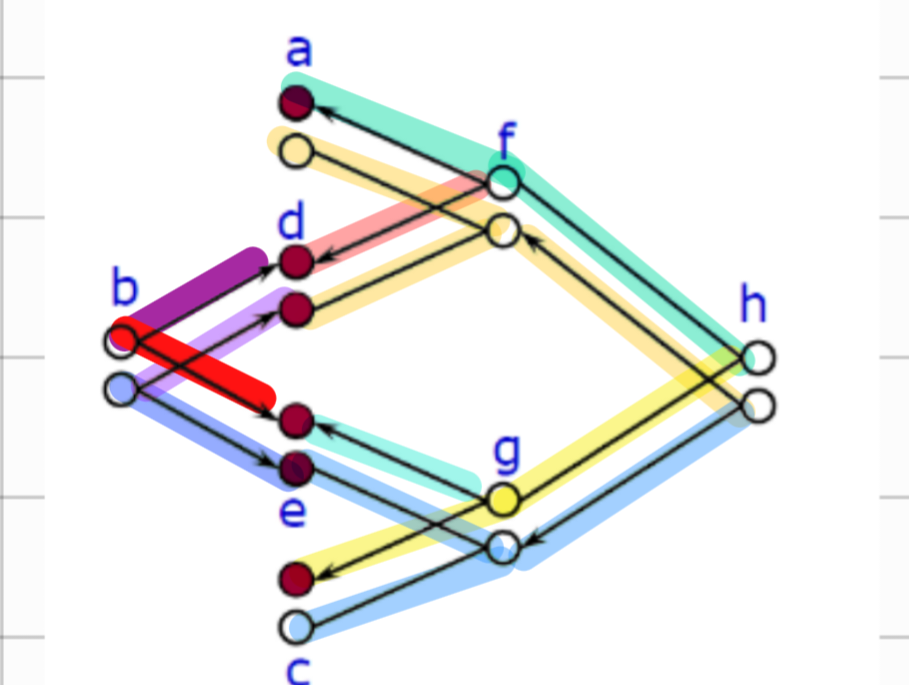
感谢“可爱的小天”的画图
可以看到,8 个故障点(3+3+2)可以有 16 个故障,其中有 10 个等效的类,所以只用 6 个测试就能完全覆盖。
5. 测试压缩
通过等效故障压缩 + 支配故障压缩,仅需考虑任意 n 输入门上的 n+1 个故障。
测试压缩指的是在不减少故障覆盖率的前提下, 减少测试模式数量的过程。
等效故障压缩和支配故障压缩可用于辅助测试压缩。
[! important] 定理 在无扇出的组合电路中, 任何能检测所有原始输入端的固定型故障的测试集, 都能检测所有固定型故障。
我们定义所有原始输入和所有扇出分支的集合称为电路的检查点。
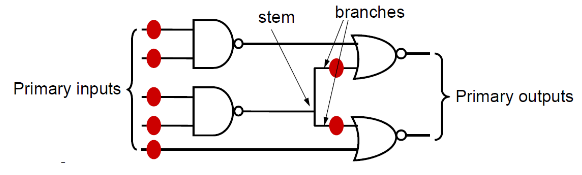
定理
组合电路中检测所有检查点(checkpoints)的单/多固定型故障即可覆盖全部故障。换句话说,检查点上的故障是覆盖全电路故障的最小关键集合。
6. 故障仿真
6.1. 仿真类型
仿真指的是对设计、其功能及性能进行建模的过程。
仿真有两种类型:
- 编译仿真:适用于零延迟组合逻辑,也用于逻辑验证的周期精确同步时序电路。对高活跃度电路高效, 但对低活跃度电路效率低下。可使用高级 (如 C 语言) 模型。
- 事件驱动仿真:仅对带有输入事件的逻辑门或模块进行评估 ( 事件指信号变化 )。可精确仿真延迟以进行时序验证。适用于低活跃度电路的高效仿真。可扩展用于故障仿真。
6.1.1. 编译仿真
- 第一步:将组合逻辑分层,并用可编译的编程语言进行编码;
- 第二步:初始化内部状态变量 (触发器)
- 第三步:对于每个输入向量,设置主要输入变量,重复 (直到达到稳态或最大迭代次数),执行编译后的代码,报告或保存计算变量。
6.1.2. 事件驱动仿真
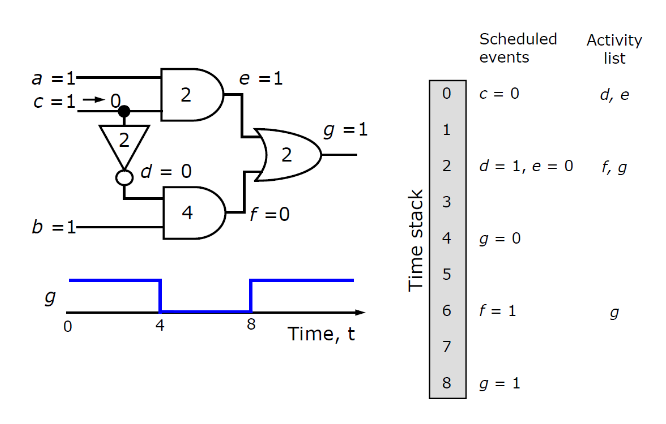
随着时间规划事件,并输入到组合逻辑中。
相较于编译代码,速度提升可达十倍甚至更高; 在大型逻辑电路中, 约 0.1% 至 10% 的门电路会因输入变化而激活。
6.2. 故障仿真定义
故障仿真的目的是对存在故障的电路进行仿真。
故障仿真的目标:
- 确定给定测试的质量;
- 生成故障诊断所需的信息 (即芯片中故障的定位)
电路中所有可被单独访问或观测的信号线(Lines)的总数量
输入向量
6.3. 故障仿真的要素
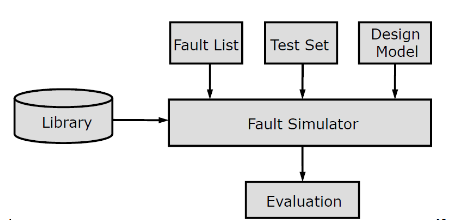
故障仿真器影响整体故障仿真的速度。
6.4. 故障仿真要点
由于单个 SAF 的数量与电路中的线路数量 L 成正比, 上述故障模拟方法的复杂度为
6.4.1. 故障压缩 Fault Collapsing
通过利用两种故障之间的关系 —— 故障等价性和故障支配性, 可以减少需要模拟的电路故障版本数量。
6.4.2. 故障排除 Fault Dropping
当进行故障模拟仅用于计算故障覆盖率时, 可通过故障排除进一步加速故障模拟过程。
故障排除是一种实践, 即在模拟任何后续向量之前, 将从故障列表中删除由向量检测到的故障。故障模拟复杂度的降低源于每个向量所需模拟的平均故障数量的减少。
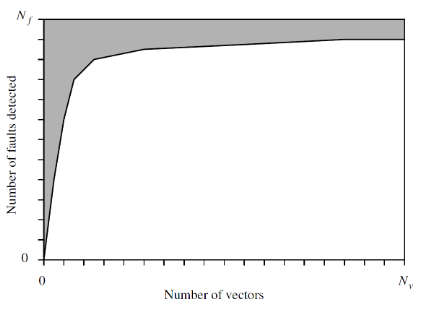
6.5. 故障仿真范式
- 故障仿真。通常而言, 在存在故障的情况下对电路进行仿真被称为故障模拟
- 故障模拟的主要目标。衡量测试模式的有效性;指导测试模式生成程序;生成故障字典。
- 故障模拟输出。故障覆盖率,测试向量检测到的建模故障的分数(或百分比);未检测到的故障集合
6.6. 故障仿真场景
- 电路模型:混合级
- 主要是逻辑,有一些开关级用于高阻抗 (Z) 和双向信号
- 信号状态:逻辑
- 两种状态(0、1)、三种状态(0、1、X)、四种状态(0、1、X、Z)等。
- 时序:
- 零延迟。对于没有反馈的组合电路
- 单位延迟。它可以保持信号变化的正确顺序。
- 多延迟
故障主要是单个卡住故障,有时是卡住开路、转换和路径延迟故障; 模拟电路故障模拟器尚未普遍使用。
单固定错误的等效故障压缩和故障排除。可以抑制故障排除以进行诊断
故障采样。当电路较大时,仿真故障的随机样本。
7. 故障仿真范式
7.1. 串行故障仿真
首先仿真无故障电路并保存所有测试向量下的正确响应。对故障列表中的每个故障重复以下步骤 :
- 故障注入:修改网表,注入当前要模拟的故障
- 故障模拟:使用测试向量集对修改后的电路进行模拟
- 响应比较:将每个测试向量下的响应与之前保存的无故障响应比较
- 检测判断:一旦发现响应不同,立即标记该故障为可检测,并跳过剩余向量的模拟
优势
- 易于实现; 仅需一个真值模拟器
- 所需内存较少 缺点
- 大量重复计算;
- 对超大规模集成电路而言,CPU 时间消耗过大
替代方案,同时仿真多种故障。
7.2. 并联故障仿真
假设仿真电路仅由逻辑门构成, 且所有门具有相同的延迟;信号仅取二进制值 ( 0 和 1 )。
利用数字计算机中逻辑运算的位并行性。对于 32 位机器字,整数由 32 位二进制向量组成。涉及两个字的逻辑 AND 或 OR 运算对所有相应的位对同时执行 AND 或 OR 运算
存储要求:每行一个字,用于双态仿真。
如果计算机字长为 N, 那么也会生成 N‐1 个故障电路的副本,1 位用于无故障电路的仿真 —— 对于电路中总共 M 个故障,
相对于串行的加速比为
缺点:无法精确模拟信号上升和下降的延迟;不适用于非布尔逻辑电路。
7.3. 并发故障仿真
同时模拟无故障电路和所有故障电路,通过共享无故障电路的仿真结果,仅记录故障电路中的差异部分。
每个逻辑门维护一个差异列表(Difference List),记录哪些故障会导致该门的输入/输出与无故障电路不同。列表元素包含故障 ID 、门输入与输出值, 以及内部状态 (如有)。
所有无故障及故障电路的事件均被隐式模拟。比其他方法更快, 但占用内存最多。
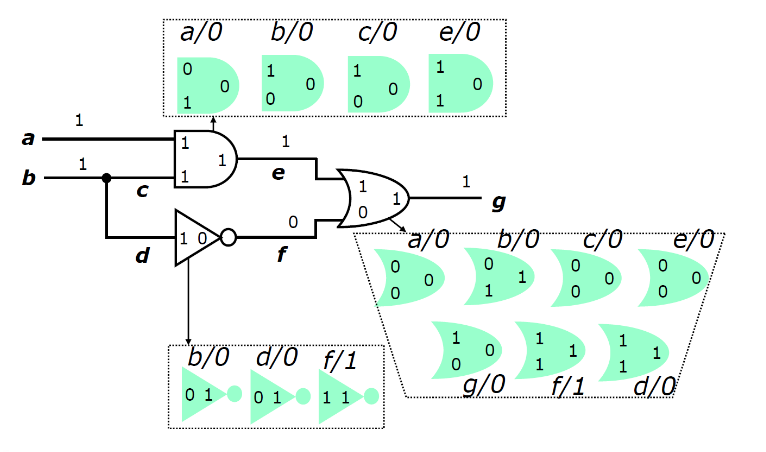
并发故障仿真仅展开相对电路其余部分而言具有不同故障影响的电路部分。换句话说, 在考虑所有故障的情况下, 仅重复有故障传播过来的门, 门的重复次数等于传播到门输出的故障数, 每个被重复的门必须通过导致该重复的故障来确认。
7.4. 演绎故障仿真✨
仅仿真无故障逻辑电路的行为,每个测试模式只需一次遍历。每个故障电路中的所有信号值均从无故障电路值和电路结构推导得出。对于每个测试模式, 从输入到输出按层级顺序 (针对组合逻辑) 对所有线路应用演绎推理过程。
对于电路中的 信号线 A,其故障列表
- 所有 在当前逻辑状态下 能导致 A 的信号值与无故障值不同 的故障名称或索引。
- 通常针对 固定型故障(Stuck-at Faults),如 A stuck-at-0A stuck-at-0(SA0)或 A stuck-at-1A stuck-at-1(SA1)。
故障列表需要从主输入(PIs)传播至主输出(POs),为每条信号线生成一个故障列表, 并随着电路逻辑状态的每次变化而进行必要的更新。
故障列表变更时触发事件列表。
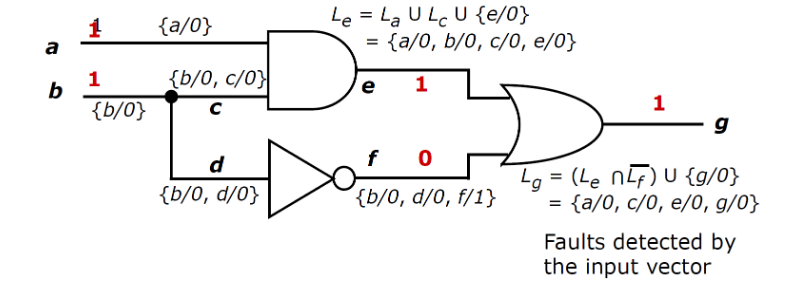
这里或门,是取
下面是故障表传播值,
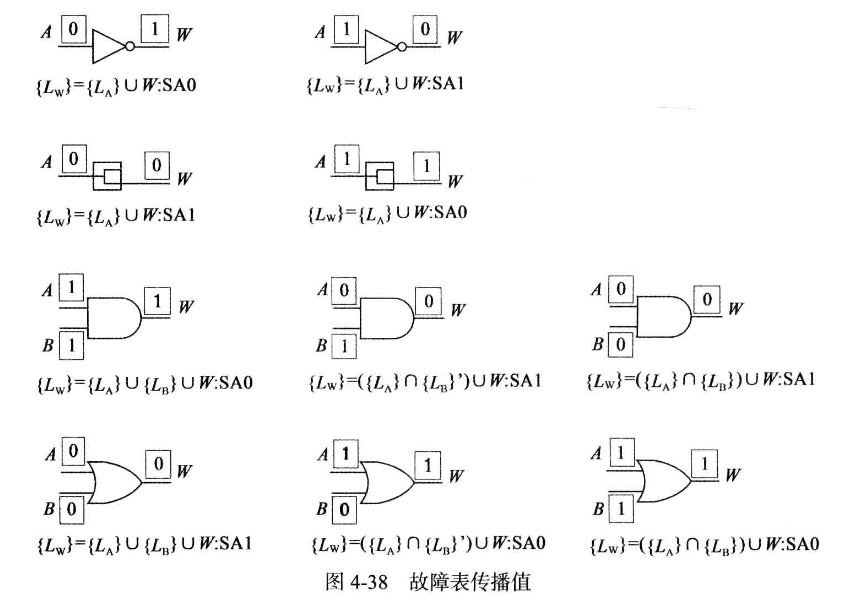
如果需要
8. 功能测试与结构测试
测试向量 ( 生成后的) 是用于数字系统的流片后测试。由于数字系统的复杂性、必要测试的规模以及测试质量因数等原因, 测试向矗生成采用的是自动方法, 该过程被称为自动测试向量生成 (Automatic Test Pattern Generation, ATPG ), 也简称为测试生成。
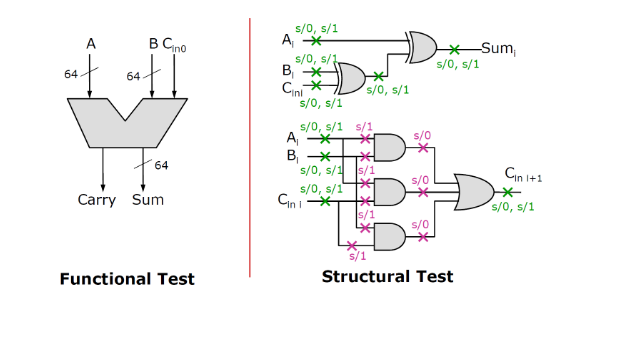
功能测试就是为电路输入输出组合生成完整的测试集。129 个输入需要
结构测试只需要 64 位切片,每个切片包含 27 个故障,最多只需要测试
8.1. 电路与二元决策树
所有 ATPG 程序都需要一个描述测试模式搜索空间的数据结构
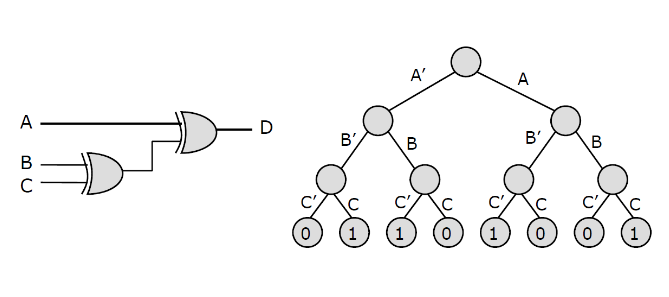
8.2. 布尔差分
布尔差分的目的是发现用于测试的输入向量。正常电路与故障电路的异或运算就是该布尔差分的方程, 针对该给定故障的测试就是使布尔差分为 1 的输入向量。
香农展开定理核心思想:
任意布尔函数 f(x1,x2,…,xn) 可以基于某个变量(如 xi)展开为两个子函数的线性组合。
公式表达:
对变量 xi 展开:
其中:
- 用于逻辑函数的简化、电路分解或测试生成(如布尔差分法)。
布尔差分法是一种形式化数学工具,用于生成数字电路中特定故障的测试集。其核心是通过比较无故障电路和有故障电路的输出函数差异,直接计算出能检测该故障的所有输入组合。
假设正常电路输出函数为
[! tip] 异或运算
[! example] 例子参考 3. 测试、测试向量
8.3. 单路径敏化
核心定义 单路径敏化是一种结构性测试生成方法,通过选择一条从故障点到主输出的路径,确保故障效应(错误信号)能沿该路径传播至输出端。其核心步骤包括: 2. 故障激活(Fault Activation) 3. 故障传播(Fault Propagation) 4. 线值确认(Line Justification)
关键概念
- 故障激活:
在故障点 ll 设置与故障值相反的逻辑值,使故障效应显现。- 例如:故障为 l SA0,则需设置 l=1。
- 敏化路径:
从故障点到主输出的路径,路径上所有门的控制输入需设置为非屏蔽值(Non-Blocking Value),使得错误信号能逐级传递。- AND门:其他输入置1(1为传递输入值的非屏蔽条件)。
- OR门:其他输入置0(0为传递输入值的非屏蔽条件)。
- 线值确认:
反向推导输入值,确保故障激活和传播的条件一致(无矛盾)。
9. 时序电路测试
时序电路除了具有记忆功能外, 还包含组合逻辑。对时序电路中的故障进行测试, 需要一系列向量, 这些向量将电路初始化为已知状态。激活故障, 并将故障效应传播至主输出端。
时序电路 ATPG 方法
- 时间帧扩展方法
- 基于仿真的方法
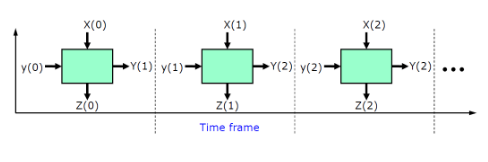
9.1. 时间帧拓展方法
本节介绍一种时序电路测试生成技术, 它将被测时序电路扩展为几个时间帧并将 D 算法应用于该电路。
同步时序表示为,
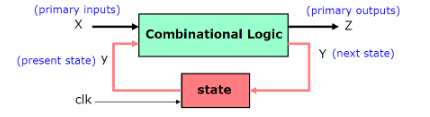
时间帧的概念,