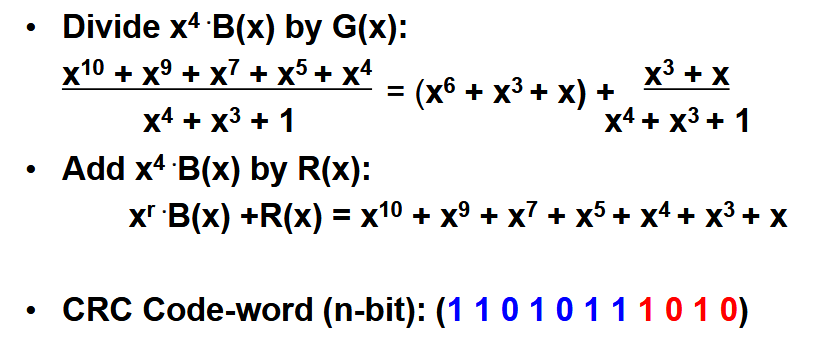1. 数据编码基础知识
数据编码包含错误检测编码、错误纠正编码以及数据的加密和解密。
错误检测编码主要包括奇偶校验码、循环冗余校验码和定重码(m-out-of-n code)。 错误纠正编码主要为海明码
2. 完全自检电路
- 故障安全电路(Fault-Secure Circuit):对于给定故障集合中的任何故障,电路绝不会产生错误的合法码字。即使存在故障,若输出仍为码字(如 m-out-of-n 码中的有效码字),则结果必定正确。
- 自测试电路:对于给定故障集的每一个故障,电路在输出处至少为一个输入码字生成一个无效码字。
全自检电路(Totally Self-Checking Circuit)则是需要同时满足故障安全和自测试的要求,即每个故障都会导致在输出码字中产生无效码字(故障的可检测性)以及始终能够输出正确的码字。
2.1. 双轨检查器
完全自检电路有两个输出,当两个输出不同时(01 或 10)是合法的,相同则说明输入为无效码字或者检查器自身出现了错误。
| 00 | 00 | 00 |
| 11 | 00 | 01 |
| 10 | 01 | 10 |
通过叠加的方式也能构建多级树检查器检测更多输入位。
3. 奇偶校验码✨
奇偶校验位检查是信道编码最简单的例子,通常用于检测单个比特的错误。在数据中添加一个奇偶校验位,使得数据位中的二进制值的总和(包含奇偶校验位)为奇数或偶数,从而实现基本的错误检测。
在通信使用前需要确认使用奇校验还是偶校验。
| 奇校验 | 偶校验 |
|---|---|
1 的总位数为奇数 | 1 的总位数为偶数 |
3.1. 校验位计算
对于一个 n 位字符串,奇偶校验位的计算方式如下:
奇校验校验位计算式
指向原始笔记的链接
偶校验校验位计算式
指向原始笔记的链接
3.2. 错误信号检验计算
对于接受方来说,通过同样的方式来进行检验。
奇校验错误信号检验计算式
指向原始笔记的链接
偶校验错误信号检验计算式
指向原始笔记的链接
如果 E=0 说明没有错误,如果 E=1 说明有错误。
3.3. 硬件设计
主要的考量就是异或延迟,对于并行和串行有不同的设计。
并行设计:
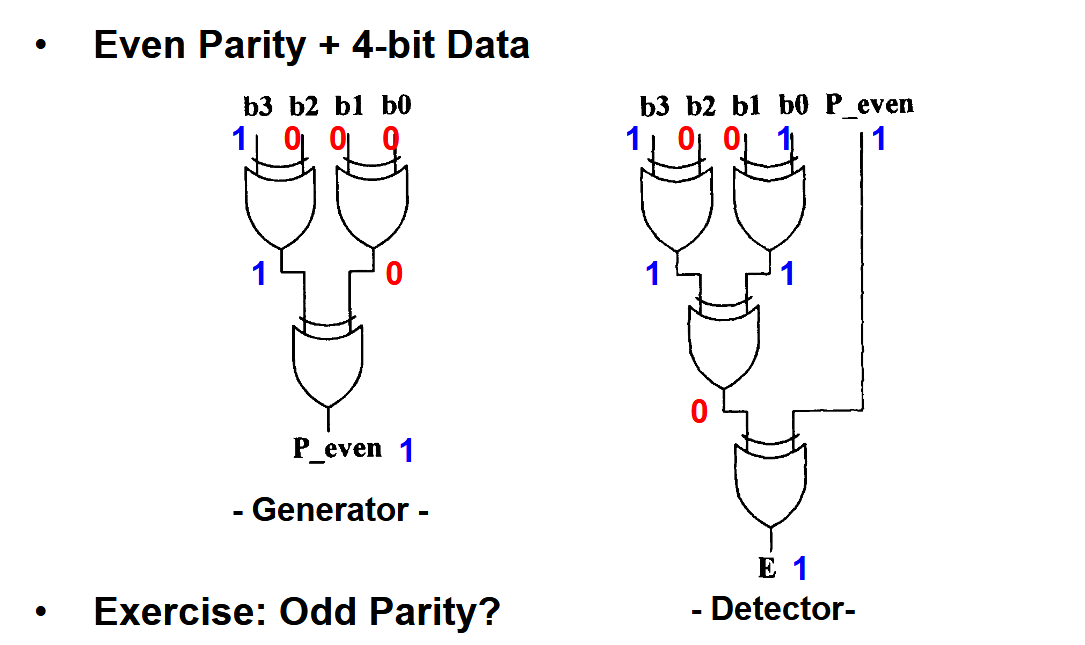
串行设计:
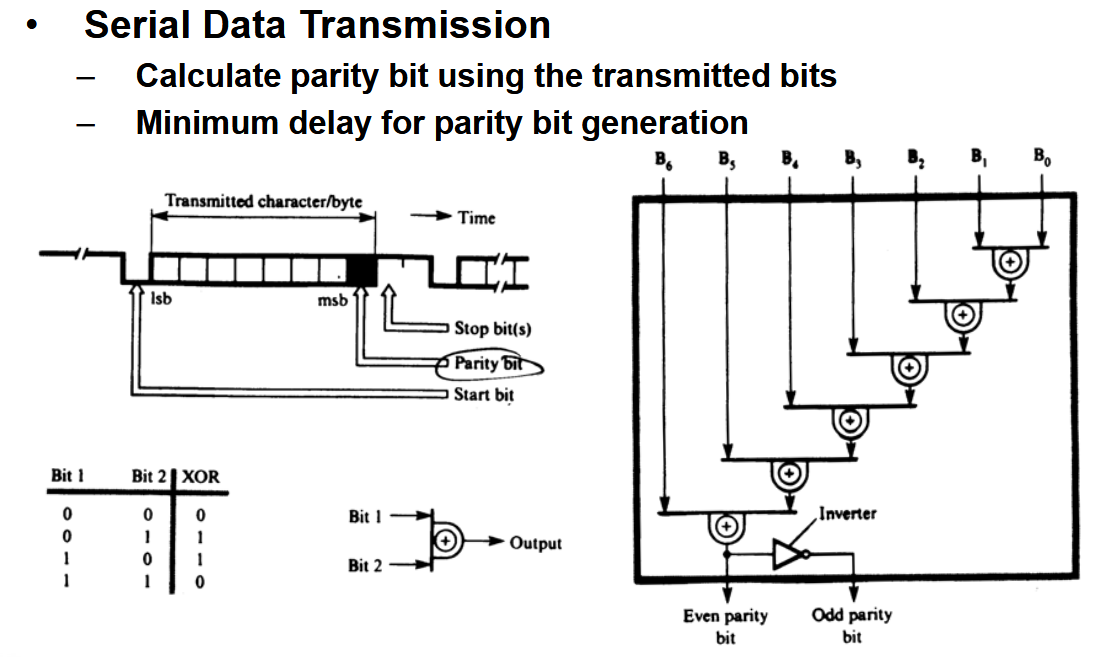
3.4. 优缺点
| 优点 | 缺点 |
|---|---|
| 在计算机系统中广泛使用 – 每个位都经过不同的路径 – 将检测到一条错误路径 | 覆盖范围太低,仅检测到 50% 的多位或突发错误。 |
| 能够检测任何单位(或者说奇数个)错误 | 无法检测到任何偶数个位错误 |
| 奇偶校验位所需的额外存储空间 |
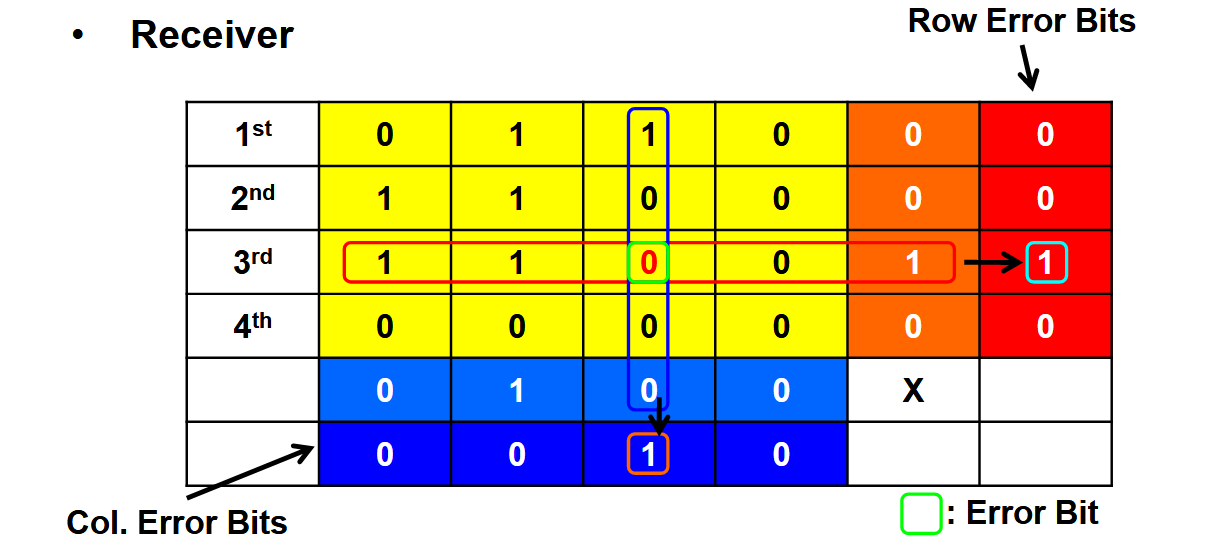
4. 2-D 奇偶校验
2-D 奇偶校验在奇偶校验的基础上,新增加了列的奇偶校验位,由此能够识别并且纠正单个位的错误。也能检测多位,但是无法确定位置并纠正。
5. 海明编码
5.1. 基础概念
海明距离
海明距离指两个码字之间不同元素的数量。
指向原始笔记的链接
最小海明距离
最小海明距离是指一组码字之间最小的海明距离,这个衡量了这组码字的检错能力。
指向原始笔记的链接
5.2. 海明码✨
对于 m 位的码字,海明码加入了 k 位的奇偶校验码,并满足
将整体码字从 LSB 开始,按照 1 到
| 数据位位置 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 编码后数据位置 | M15 | M14 | M13 | M12 | P5 | M11 | M10 | M9 | M8 | M7 | M6 | M5 | P4 | M4 | M3 | M2 | P3 | M1 | P2 | P1 |
| 奇 | 偶 | 校 | 验 | 位 | 覆 | 盖 | 率 | |||||||||||||
| P1 | X | X | X | X | X | X | X | X | X | X | ||||||||||
| P2 | X | X | X | X | X | X | X | X | X | X | ||||||||||
| P3 | X | X | X | X | X | X | X | X | X | |||||||||||
| P4 | X | X | X | X | X | X | X | X | ||||||||||||
| P5 | X | X | X | X | X |
不同位置的奇偶校验码覆盖的范围不同,对于在
题解如下。对于例如对于一个 5 位的信息,要用偶校验和海明码实现一位错误的检测。
| M5 | M4 | M3 | M2 | M1 |
|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 |
要实现海明码,首先需要计算 k,使得
| 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| M5 | P4 | M4 | M3 | M2 | P3 | M1 | P2 | P1 |
| 1 | 1 | 0 | 1 | 0 | ||||
| 1001 | 0111 | 0000 | 0101 | 0000 |
将所有二进制进行偶校验,
这就是对应位置的校验码。
| 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| M5 | P4 | M4 | M3 | M2 | P3 | M1 | P2 | P1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
如果需要进行两位检测,再加一位对所有位的偶校验即可。
5.3. 错误检测
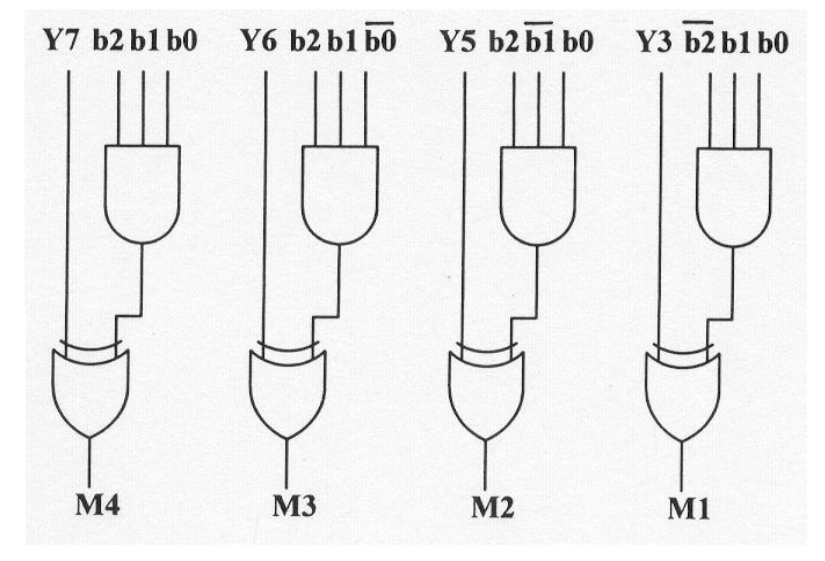
海明码的错误检测是通过奇偶校验位直接指出的。例如对于在位置 1、2、4 的校验位 011 则说明第 3 位为错误位。
硬件实现如下:
5.4. 双位错误检测
如果要检测两位错误,则至少需要的最小距离为 4(k=4),即使用拓展海明码。在最高位增加一个额外的奇偶校验位,用于对所有位进行奇偶校验。
5.5. 海明码能力总结
| 最小距离 | 能力 |
|---|---|
| 1 | 无法进行错误检测 |
| 2 | 单位检测 |
| 3 | 单位纠错 |
| 4 | 单位纠错和双位检错 |
- 对于 k 位的错误检测,最小距离
- 对于 k 位的错误纠正,最小距离
| 最小距离 | 纠错 | 检错 | 检测 |
|---|---|---|---|
对于 m 位码字+k 位纠错码的码字
- 编码效率 =
- 编码冗余=
6. 循环冗余编码 Cyclic Redundancy Check
6.1. 基础知识
6.1.1. 位置多项式表示法
一个数的位置和多项式表示法
一个数的位置和多项式表示法
一个数用位置表示法表示为
「.」:radix point,小数点。在小数点之前的是整数位(integer digits),在其后的是小数位(fractional digits)。 「r」:radix base,称为底数或者进制。 「 」:是最高位(most significant digit, MSD) 「 」:是最低位(least significant digit, LSD) 其位置多项式可以表示为
指向原始笔记的链接
6.1.2. 模 2 运算
模2运算是用于CRC的错误检测逻辑而设计的,并非用于数值计算。其特点在于:
- 每一位单独计算,没有进位也没有借位;
- 减法和加法等同(都是异或实现);
6.2. 原理
通过使用模 2 运算计算多项式除法,有以下的性质:
对于一个多项式
这里
这说明对于信息
6.3. CRC 码生成✨
所以要构造 CRC 码的核心就是得到
Example
对于
和 ,生成最后的 CRC 码。分别用多项式和 2 进制数进行演示。 多项式形式
为 (把 0 项写出来方便解释,实际运算中省略),已知 的最高项为 ,则有 。构造新信息多项式 。
验证也很简单,就是用得到的
[! info] 对于 CRC 码的完整证明需要了解多项式环(抽象数学中的一个领域)的因式分解特性。
6.4.
生成多项式
6.4.1. 规则 1:错误多项式不能被整除
若错误多项式
6.4.2. 规则 2:检测所有短突发错误
生成多项式如果不含
6.4.3. 规则 3:检测所有奇位数突发错误
6.4.4. 标准的
这里看看了解即可。
| CRC codes | |
|---|---|
| CRC-12 | |
| CRC-16 | |
| CRC-CCITT | |
| CRC-32 |
6.5. 电路设计
电路设计是最能体现循环冗余码名称含意的地方。通过移位寄存器就能实现 CRC 码的生成。首先介绍一下循环移位寄存器。
6.5.1. 循环移位寄存器
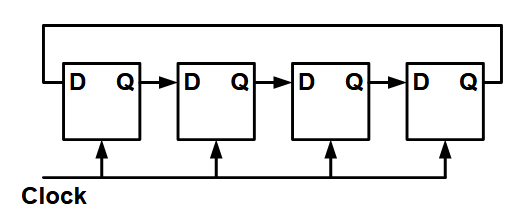 这就是一个基础的循环移位寄存器。输入一般是从左到右输入,输入的数字就不断在其中循环。如果在反馈路径上添加一个 XOR,那么就能使得循环的位模式变化。
这就是一个基础的循环移位寄存器。输入一般是从左到右输入,输入的数字就不断在其中循环。如果在反馈路径上添加一个 XOR,那么就能使得循环的位模式变化。
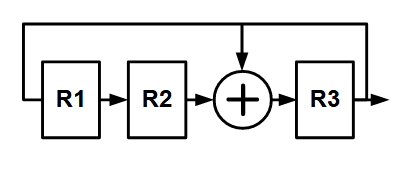
6.5.2. 最大长度移位寄存器
如果一个 n 位的反馈移位寄存器能产生
为什么最大长度移位寄存器能作为分频器?
因为其输出信号具有长周期特性,其频率为输入时钟的
,分频系数为 。
6.5.3. 余数生成
循环码生成的时候,输入和输出都是大端序(MSB)。对于 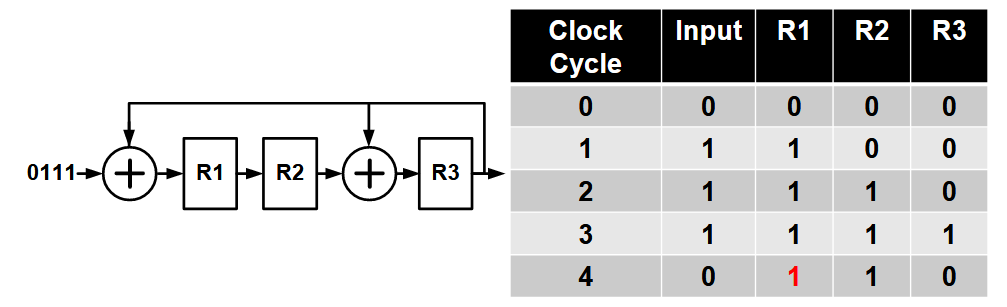 将
将 1110 按照大端序输入最大长度移位寄存器中,当所有输入都进入到寄存器之后,寄存器中的值就是 011,
[! note] 这里在列情况的时候,可以先把每个寄存器运算式写出来,例如,
这里
是当前时刻的值, 是上一时刻的值。这样方便检查和运算。
6.5.4. 多项式除数电路
对于
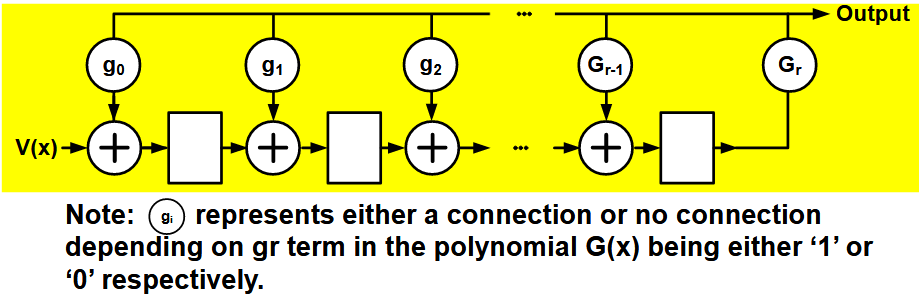
6.5.4.1. 减少移位周期
如果
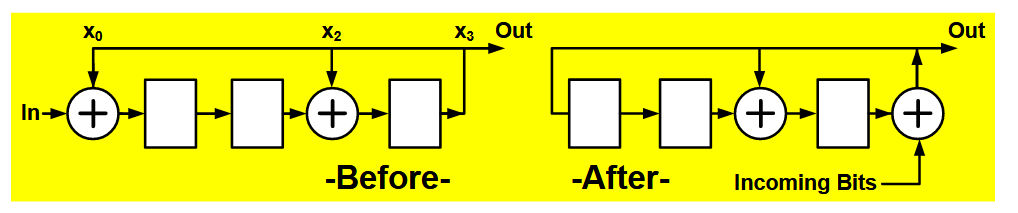
原本需要输入
6.5.5. 编码电路
对于一个 CRC 编码,其构成为
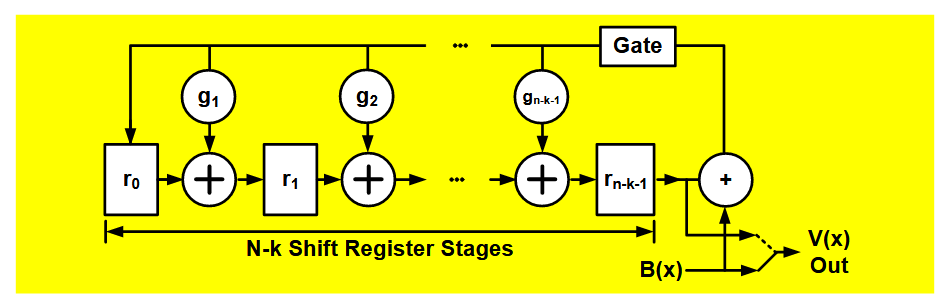
编码电路在多项式除数电路的基础上增加了一个门(gate)和一个 2 门 MUX。门和 MUX 在前 k 的位都是打开的,这样信息位就能输入多项式除数电路和输出端口;后 n-k 位就需要关闭门和 MUX,使得移位寄存器中的检查位输出。
7. 平均字长✨
这里会给出多种情况的概率,然后需要根据概率计算平均传输次数,然后乘以码长就得到的平均字长。
对于海明码和 CRC 码,具有不同的性质:
- 海明码能纠错 1 位;
- CRC 只能检错;
下面给出例题和解答过程。
假设,出错 1bit 的概率是 a,出错 2bit 的概率是 b,并且最多出现 2bit 错误。如果检测到错误,最多再传输 2 次。
对于海明码而言,传输成功的概率是 1-b,令其为
随后再乘以码长就能得到平均字长。
对于 CRC 码而言,传输成功的概率是
再乘字长就能得到平均字长。
8. M-out-of-N code
m-out-of-n 码是指码字长度为 n 位时,每个有效码字正好包含 m 个 1 和 n-m 个 0。单个位错误将导致码字出现 m + 1 或 m – 1 个 1。
8.1. 附加法和定重码
最简单的方式就是在原始数据的后面直接附加代码,使得总的 1 的数量满足设计需求。
另外一种定重码就是为每一位码位赋予权重。
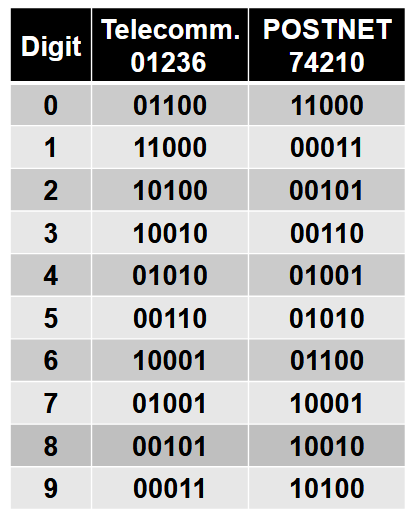
8.2. M-out-of-N 码检查器
对于有效的 m-out-of-n 代码输入,检查器的输出为 01 或 10。如果输入的 1 的个数大于或小于 m(无效的输入),则输出为 11 或 00。码字包含相同个数的 1 和 0 ,即 n=2m,这种类型的码称为 k-out-of-2k 码。先从 k-out-of-2k 码的检查器开始设计。
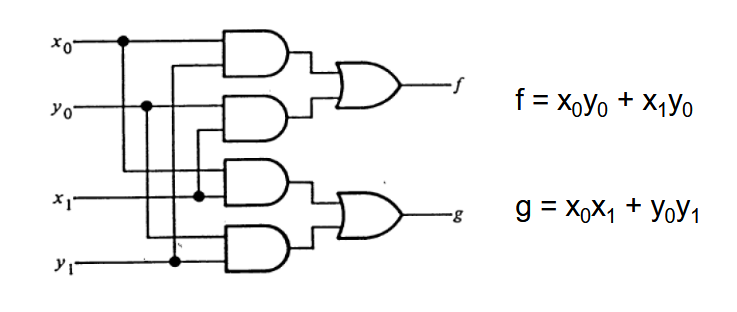
8.2.1. k-out-of-2k 码的检查器
首先将 2k 位分成等大小的 A 和 B 两组,
检查器的输出
这个公式有点抽象。
[! Tip] 一些函数设计小规律 假设
,
,说明无论 A 中的 1 有多少,T 始终为 1; ,说明 A 中存在 1 个 1 的时候,T 始终为 1; ,说明 A 中任意两个元素为 1 的时候,T 始终为 1; ,说明 A 中任意 3 个元素为 1 的时候,T 始终为 1; ,说明 A 中全部 4 个元素为 1 的时候,T 才能为 1。
8.2.2. M-out-of-N 检查器
对于一个一般的 m-out-of-n 检查器,可以通过将给定的码字转换为 1-out-of-
这里的核心实际上就是找到合适的 k 值。这个 k 值需要满足,
组合数计算,
Question
后面的给的示例没有看出什么规律,不是很懂。