1. 引入
当电路存在电压的时候，就会形成电场耦合；当电路存在电流的时候，就存在磁场耦合。于是当两个电路靠得非常近的时候，就会产生串扰。
串扰会对相邻电路产生噪声，由此导致信号完整性下降、减少噪声容限。
1.1. 并联微带线
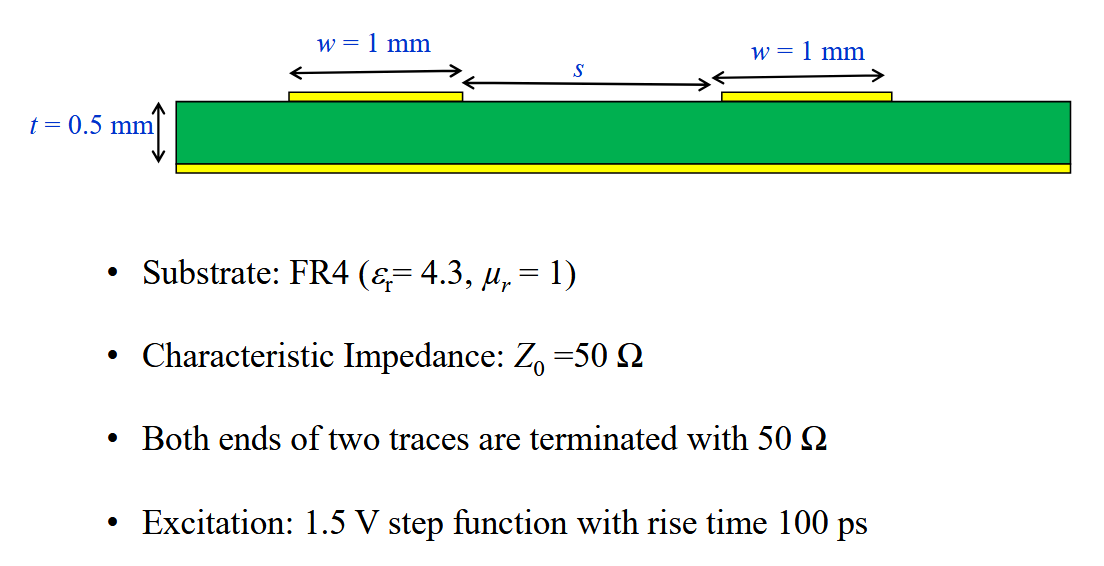
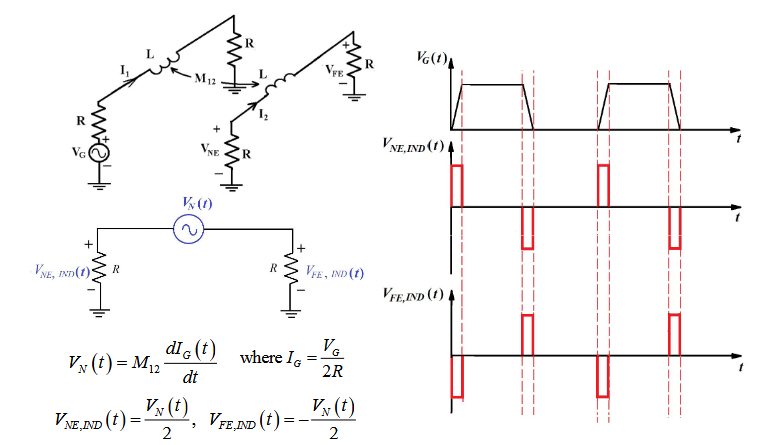
当电压增加的时候，会造成干扰。
2. 频域串扰分析
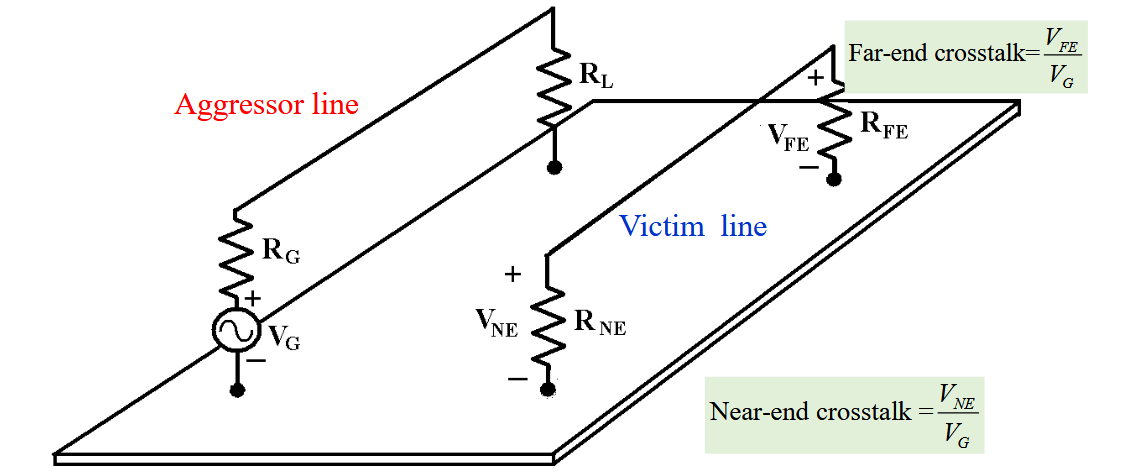攻击线在受害线的两端观察到串扰信号。
- Near End：受害线更靠近攻击线的电源的一端。
- Far End：受害线更远离攻击线电源的一端。
需要分析的就是攻击线路导致的
2.1. 平行线的分布参数
我们需要知道平行线的分布电感和电容来确定串扰。RLCG 模型，R 是串联的电阻，L 是自感和互感，C 是自容和互容，G 是连接到地的电阻。
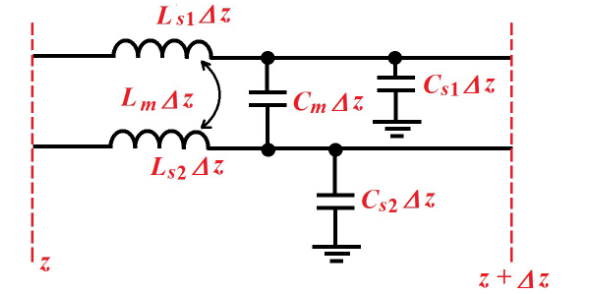
- Ls1 = 导体 1 单位长度的自感 (H/m)
- Ls2 = 导体 2 单位长度的自感 (H/m)
- Lm = 导体 1 和 2 之间单位长度的互感 (H/m)
- Cs1 = 导体 1 单位长度的自电容 (F/m)
- Cs2 = 导体 2 单位长度的自电容 (F/m)
- Cm = 导体 1 和 2 之间单位长度的互电容 (F/m) 在分析串扰的时候，我们更关心自感、互感和自容、互容。
为了简化分析，这里假设了频率足够低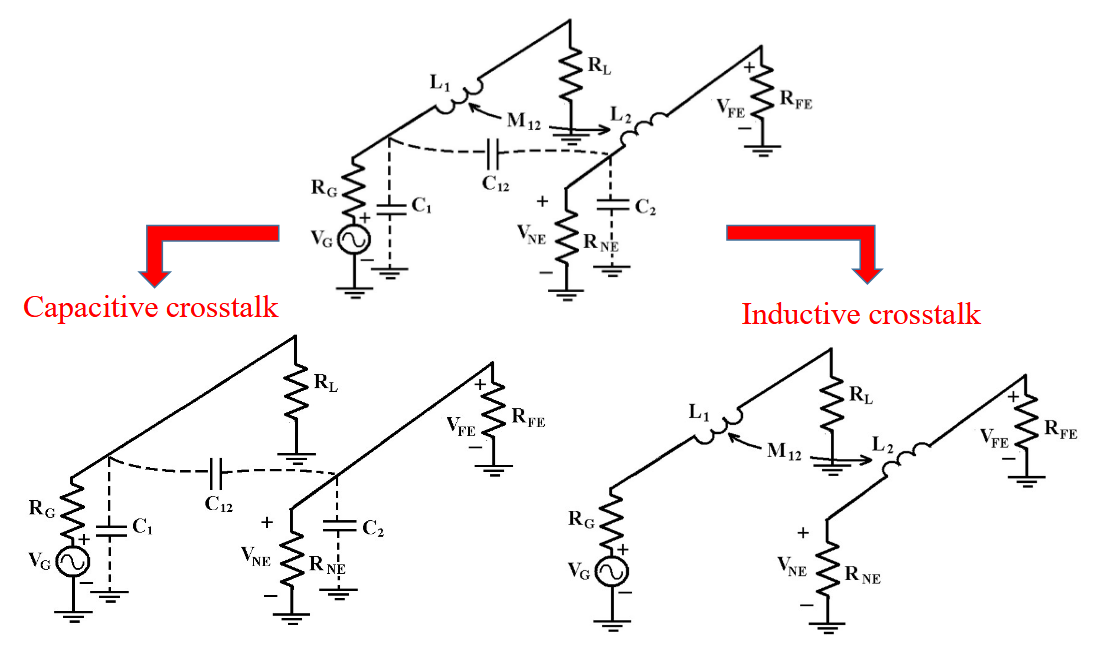 
通过单位电容、单位电感和长度就能计算出自自容、自感等，
2.2. 电容串扰
大多数情况下，两条平行线具有相同的分布参数和终端电阻。即假设所有电阻相同以及电容相同。
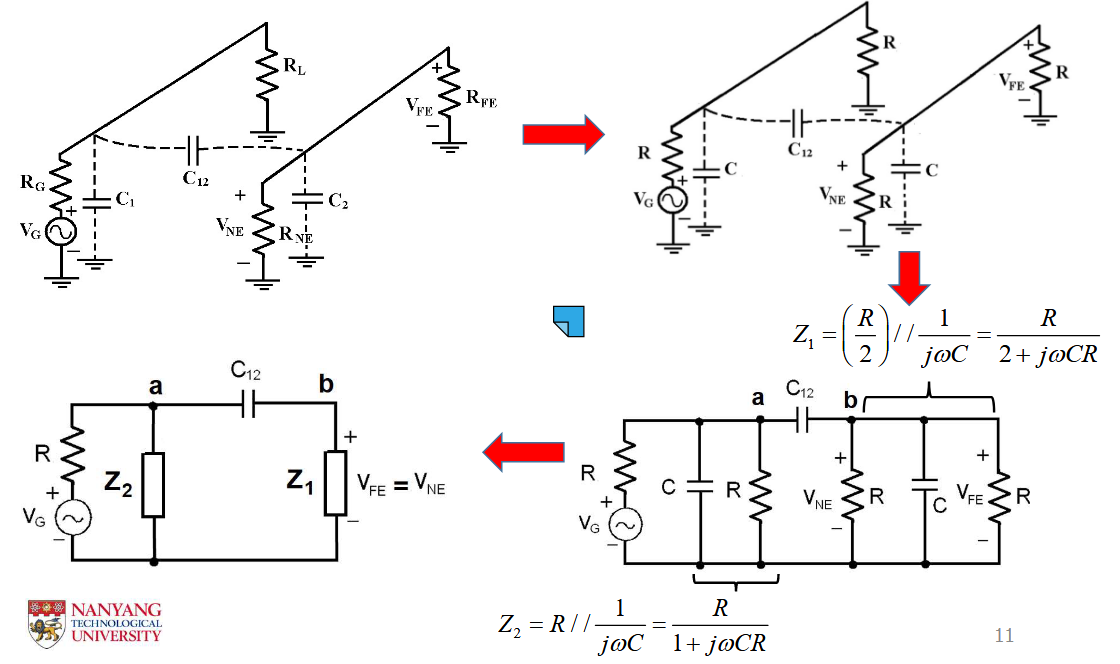
由此能分析出来，由于电容串扰产生的干扰为，
可以看到这个公式的分母由三个部分组成，并且分别是，不和频率相关，和
- 当低频时，第一项为主，其他项可忽略
- 当频率增加，第三项为主，其他项可忽略；
- 当频率增加地更多，第二项为主，其他项可忽略。
但是这个界限在哪？我们通过对比项之间的大小可以得知。
于是可以有以下近似，
在
2.2.1. Exercise 1
“Determine the near-end and far-end capacitive crosstalk for the two parallel microstrip lines at 100 kHz and 10 MHz for: (a) RG = RL = RNE = RFE = 10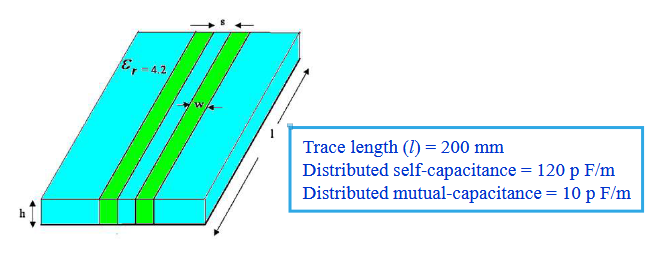 
2.2.2. 电容串扰特性
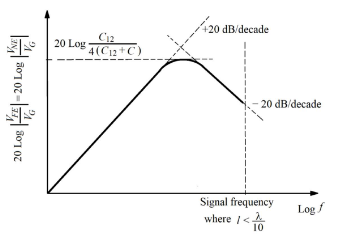
- 近端和远端电容串扰具有相同的幅度和同相。
- 电容串扰随频率以+20dB/十倍频程的速率增加，在特定频率处达到最大值，然后随频率以+20dB/decade 的速率减小。 –20dB/十年。
- 具有高阻抗端子的电路更容易受到电容串扰的影响
2.3. 电感串扰
和电容串扰类似，
- 当
低的时候， 主导； - 当
增加的时候， 主导串扰； - 当
继续增加的时候， 主导串扰；
所以，我们也能在不同频率下来近似计算。
当
当
所以有，
当
当
当
2.3.1. 电感串扰特性
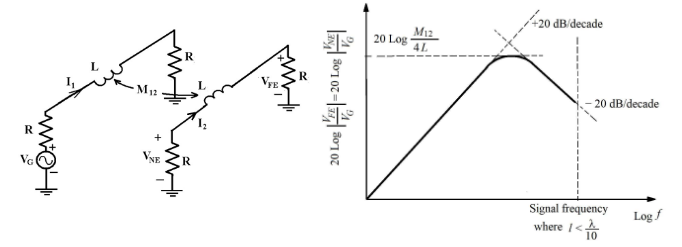
- 近端和远端感应串扰异相（注意：观察接地电压的极性）。
- 感应串扰随频率以+20dB/十倍频程的速率增加，在特定频率处达到最大值，然后随频率以-20dB/十倍频程的速率下降。
- 具有低阻抗端子的电路更容易受到电感串扰的影响。
2.4. 串扰产生的能量
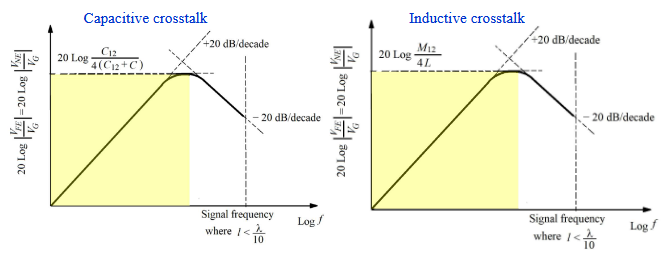通过观察电容串扰和电感串扰的频率响应，大多数能量主要集中在低频频谱中。在较高频率下，能量会恶化，因为串扰与频率成反比。较低频谱的串扰是主要问题。
同样，我们将电路分为电容串扰和电感串扰来说明，并且只考虑低频情况。此时有电容串扰为，
电感串扰为，
2.4.1. 低频电容串扰
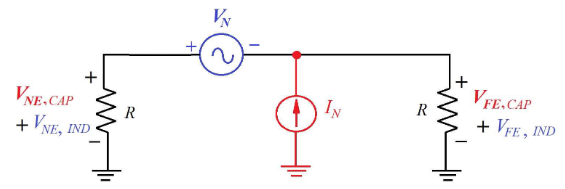
在低频下有电容串扰，
电容耦合可以被建模为从干扰源线路到受害线路的耦合噪声电流源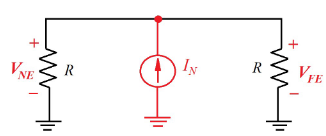 
2.4.2. 低频电感串扰
电感耦合可以被建模为从干扰源线路到受害线路的耦合噪声电压源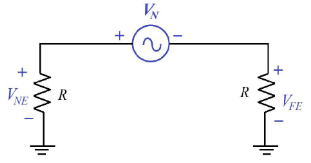 
2.4.3. 电容加电感耦合
3. 时域串扰分析
3.1. 数字信号的传播延迟
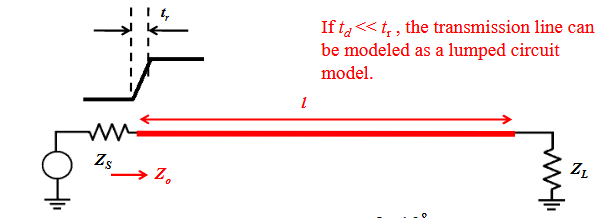信号的传播速度：
单位长度的传播延迟为，
信号的传播延迟为，
3.2. 时域串扰分析
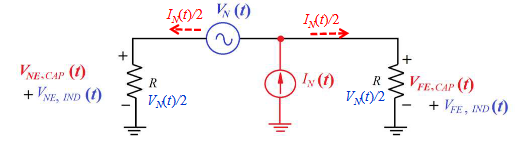
有时域串扰，
3.2.1. 时域的电容串扰
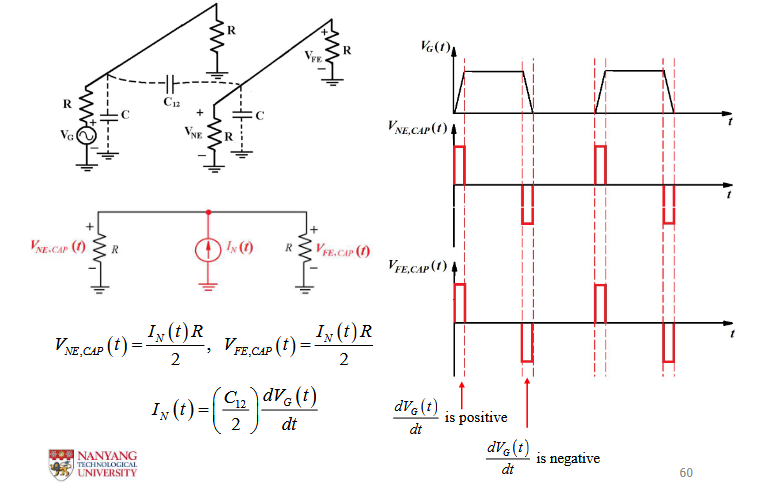
3.2.2. 时域的电感串扰
