《Chapter 1 射频干扰》笔记

Chapter 7 Antennas 笔记

1. 基本偶极天线

一般情况下，通过对天线表面的电流分布的积分能获得辐射电场和磁场。在这一章会对一些简单的天线进行研究，因为他们的在远处的辐射场和其他实际的天线的辐射场类似。

1.1. 电偶极子

电偶极子由长度为 的无穷小电流元件组成。我们假设其携带的相量电流 在沿元件长度的所有点上都具有相同的幅度和相位。

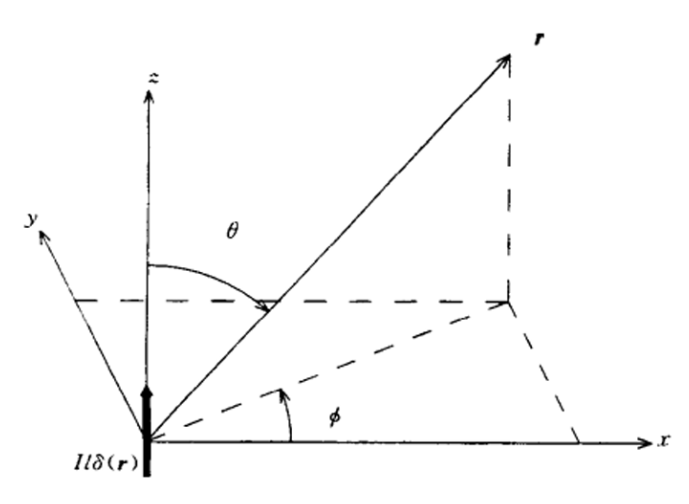
通常用球坐标系描述天线，因为从远距离天线辐射的波是球面波。该坐标系中点的位置由到该点的径向距离 ，从 轴到该点的径向线的仰角 ，以及在 平面上的投影与 轴之间的方位角 来描述。

正交单位向量 指向这些坐标值增加的方向。

1.1.1. 一般情况分析

磁场强度矢量的分量变为，

电偶极子磁场强度矢量方向角分量

指向原始笔记的链接

同样有电场强度矢量，

电偶极子电场强度矢量径向分量计算式

指向原始笔记的链接

电偶极子电场强度矢量仰角分量计算式

指向原始笔记的链接

电偶极子电场强度矢量方向角分量计算式

指向原始笔记的链接

有自由空间阻抗为 ，

自由空间波阻抗计算式

为真空磁导率常数； 为真空介电常数

指向原始笔记的链接

1.1.2. 远场情况

但是我们更加关心的是对远场的电偶极子的分析。在远场的时候， 可以被忽略。因此对于磁场强度分量和电场强度分量，可以简化为以下两个公式，即只用考虑磁场矢量的方向角分量和电场矢量的仰角分量

远场条件下电偶极子磁场强度矢量方向角分量计算式

指向原始笔记的链接

电偶极子远场条件下电场强度矢量仰角分量计算式

指向原始笔记的链接

此时的波阻抗为，

远场电偶极子波阻抗计算式

为自由空间的波阻抗。

指向原始笔记的链接

1.1.3. 近场情况

在近场情况下，则是公式中的 和 两项起主导作用。由此重写公式为，

在近场情况下，如果有 ，那说明

• 通常有两个以上的电场和磁场
• 非 0
• 波阻抗
• 此时的近场为高阻抗场或者电场

如果有 ，这对应于过渡场条件或近场和远场之间的边界。

1.2. 磁偶极子

假设有一个半径为 的小磁环，其磁偶极矩为

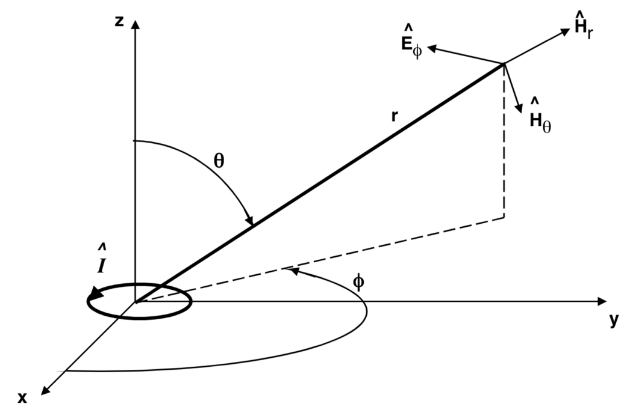
1.2.1. 一般情况分析

磁偶极子的磁场矢量和电场矢量为，

有 和

1.2.2. 远场分析

和电偶极子类似的情况，电场只用考虑方向角分量，磁场则是考虑仰角分量，其他分量为 0。

1.2.3. 近场分析

对于磁偶极子，其近场阻抗则是

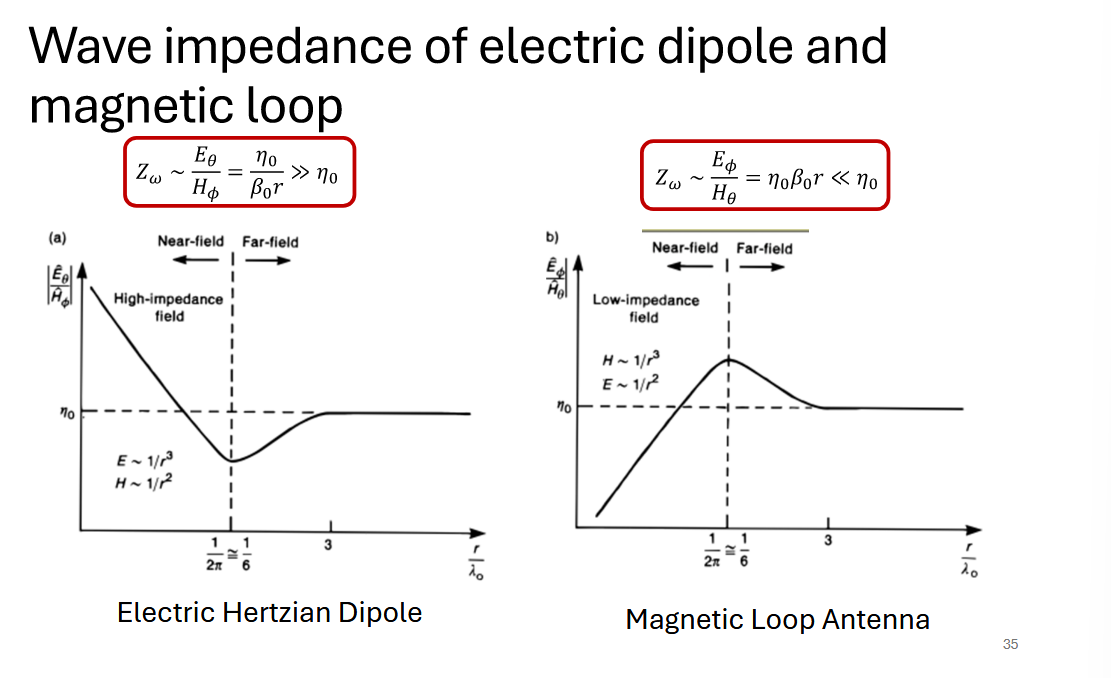
2. 近场与远场的波阻抗分析总结

2.1. 远场的波阻抗分析

对于电偶极子和磁偶极子而言，其远场的波阻抗 都可以看作是自由空间的波阻抗。

自由空间波阻抗计算式

为真空磁导率常数； 为真空介电常数

指向原始笔记的链接

2.2. 近场的波阻抗分析

当有 的时候，可以看作近场。

对于电偶极子而言，其近场阻抗为 ，此时为高阻抗场。

对于磁偶极子而言，其近场阻抗为 ，此时为低阻抗场。

2.3. 近场远场边界

对于天线长度 的小天线而言，当场距离天线的距离满足 时，此时的场可以按照远场进行分析。

大天线远场条件推导

3. 天线辐射特性

3.1. 远场天线上任意一点与源的距离近似

辐射方向图是天线辐射特性的图形表示，除非另有说明，否则它是在远场中定义的，且一般考虑沿 z 轴放置的有限长度线源。

对于远场中的天线来说，天线上任意一点与源之间的距离 可以写为

天线上任意一点与电磁波源之间的距离计算式

天线中点距离电磁波源的距离； 天线上任意一点距离天线中点的距离； 为仰角

指向原始笔记的链接

天线上任意一点与源之间的距离近似的推导

3.2. 线天线

假设现在有一个长度为 的具有均匀电流的线天线。

3.2.1. 归一化电场

对于线天线上 处任意一点，有仰角 ，代入电偶极子的电场公式电偶极子远场条件下电场强度矢量仰角分量计算式。

[! question] 在这里，slides 上给的公式的距离是 ，即天线中心到源的距离，但是前面又是考虑的 处的电流，我觉得这里有些冲突了。于是改换成 。

将其沿着 到 进行积分，由于电流 是均匀的，所以有，

将前面的近似距离代入可得，

在远场，如果有 ，那么有 和 ，代入并积分得，

有归一化电场定义，

归一化电场定义式

因此，具有均匀电流的天线的归一化电场特性为，

均匀电流天线的归一化电场特性

为波数； 为天线长度的一半； 为仰角。

指向原始笔记的链接

均匀电流线天线的归一化辐射功率特性

指向原始笔记的链接

3.2.2. 辐射方向图

主要参数有主瓣、增益、3dB波束宽度、第1零点、第1旁瓣、后瓣

3.2.3. 天线的方向性系数

方向性系数

方向性系数定义为球体上的最大功率密度与其平均值的比值。

指向原始笔记的链接

为辐射强度

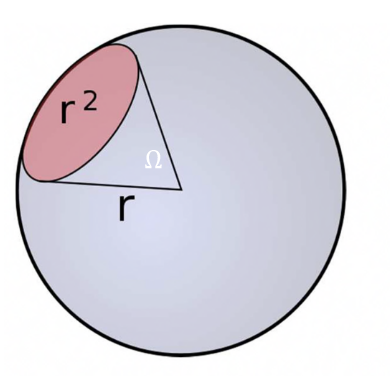
立体角 为球体表面积与半径的比值，总立体角为 球面度（），具体计算如下

平均辐射功率为，

代入方向性系数公式可得，

3.2.4. 波束面积

定义波束面积为 ，是归一化辐射功率在总立体角上的积分。由此也可重写方向性系数。

光束面积越小，方向性越大。

3.2.5. 各向同性天线

各向同性天线是一种向各个方向均匀辐射功率的理想天线。不存在实际的物理各向同性天线，然而经常被用作天线增益的参考天线。对于各向同性天线， 适用于所有角度。因此有 和 。

3.2.6. 电偶极子

对于电偶极子，有 ，，。 电偶极子归一化电场特性计算式 电偶极子归一化电场、波束面积、方向性系数推导

3.3. 其他天线

3.3.1. 偶极子天线

3.3.2. 偶极子天线

1λ 偶极子天线归一化电场特性计算式

为仰角。

指向原始笔记的链接

3.3.3. 长线天线

L是天线长度

3.3.4. 孔径天线

孔径天线方向性系数计算式

为孔径面积； 为孔径效率

指向原始笔记的链接

3.3.5. 孔径效率

孔径效率

孔径效率是衡量天线整个孔径上场分布均匀程度的指标。

指向原始笔记的链接

3.4. 天线增益

天线增益计算式

为 角上的归一化功率； 为最大归一化功率； 为方向性系数； 为天线损耗系数（天线效率）

指向原始笔记的链接

天线增益是互易的。即同一天线的发射增益与接收增益相同。

3.5. 无耗天线增益

3.5.1.1. 无损偶极子

赫兹偶极子 ， 偶极子天线 ， 偶极子天线 ，

3.5.2. 无损孔径天线

直径孔径天线，假设 100%的孔径效率

另一个 60%孔径效率的，在算有效面积的时候把效率算进去即可。

3.6. 有损天线增益

[! question] 天线增益的有损无损不包括孔径效率？

具体过程和上面一样，在计算 的时候乘上天线效率即可。

3.7. 半功率波束宽度

半功率波束宽度指增益波动小于 的波束宽度。波束宽度在两个主要平面中定义：（x-z 平面）或者 （y-z 平面）

对于长度为 的线天线，电流有，

对于具有半径 的圆孔径天线，

3.8. 波束宽度

对于高指向性天线，其方向性系数可以用下面的经验公式进行计算。

高指向性天线方向性系数经验计算式

为 处的半功率波束宽度； 为 处的半功率波束宽度；

指向原始笔记的链接

3.9. 天线类型

各向同性天线、全向天线、舷侧天线、端火天线

3.10. 例题 1a 和 1b

Example 1a

3.11. 波的传导

3.11.1. 有效辐射功率

有效辐射功率

EIRP 表示了天线在某一方向上的辐射功率，是一个在工程和通信领域中常用的参数。这个公式的目的是计算天线在特定方向上的辐射功率，考虑了发射机输出功率、天线增益以及与天线相关的损耗。

有效辐射功率计算式

为发射机输出功率； 为发射天线增益； 为发射机效率。

指向原始笔记的链接

指向原始笔记的链接

3.11.2. 远场功率密度与远场电场

远场功率密度计算式

为有效辐射功率； 为发射天线到远场点的距离。 为发射机输出功率； 为发射天线增益

指向原始笔记的链接

远场电场强度计算式

为远场功率密度； 为自由空间波阻抗； 为有效功率辐射

指向原始笔记的链接

远场电场推导

3.11.3. 接收功率与 Friss 传输方程

为远场功率密度； 为有效孔径面积； 为接收端天线的效率。由此导出 Friss 传输方程。

Friss 传输方程

为发射机输出功率； 为发射天线增益； 为接收天线增益； 为波长； 为发射天线到远场点的距离。

指向原始笔记的链接

路径损耗计算式

为波长； 为发射天线到远场点的距离。

指向原始笔记的链接

3.12. 极化损失

极化（Polarization）是指电磁波中电场矢量（电场强度）的振动方向随时间的变化方式。简单来说，极化描述了电磁波的电场如何在空间和时间中振动。极化是电磁波的一个基本特性，影响电波的传播特性和如何与物体（如天线、材料）相互作用。

指向原始笔记的链接

随后我们考虑线极化的远场端极化损失。

产生这种极化类型的天线一般都是偶极子天线、八木天线。根据线极化角度相对于地面的情况，分为垂直极化和水平极化。

计算极化损失时，考虑的是位于远场的接收端天线相对于需要接收的电磁波的极化损失。在远场时电磁波传播模式是TEM波，电场方向正交于电磁波传播方向。

如果两个天线的极化方向相同，但是位置错开，我们只需要知道接收端天线相对于电磁波传播方向的夹角就可以计算极化损失。这部分的原理非常简单，只需要知道电磁波的电场在天线位置上的投影就行。

这里的 就是入射电场 与接收端天线的夹角。所以接收端接收到的电场 为，

需要注意的是极化损失计算的是功率上的损失，接收端接收功率与电磁波在这个位置的功率关系为：

其中 是电磁波的特征阻抗， 代表的角度永远是接收端天线相对于电磁波的角度，由于已经处于远场所以和发射端关系不大。

以对数形式表示的话就是：

3.13. 圆极化的远场端极化损失计算

圆极化可以分为顺时针圆极化和逆时针圆极化，可以视为两个线极化的叠加。所以传递到线极化的话自然存在损失，这个值老印取了大约

在计算圆极化与线极化之间造成的极化损失时只需要在 的基础上额外损失 就可以了。

3.14. Example 2a, 2b, 2c

Example 2a