《匹配网络》笔记

[! tldr]

1. 使用史密斯圆图进行网络匹配

史密斯图的使用需要直尺、圆规和量角器，在考试的时候务必准备好。

1.1. 史密斯圆图基础

史密斯圆图是设计匹配网络的工具。

史密斯圆图是由反射系数 平面（所有的点都是用 来标定的）上的恒定阻抗/跨导圆（圆上具有一致的 R、X、G、B）构成，。

反射系数既可以用直角坐标系（，），也可以用极坐标 和 。

1.1.1. 阻抗/导纳归一化

史密斯圆图上所有的数据都是经过归一化的。

归一化阻抗计算式

为线路的负载阻抗； 为传输线的特征阻抗； 为传输线电阻； 为传输线电抗

指向原始笔记的链接

类似的还有导纳的归一化，

归一化导纳计算式

为负载导纳； 为特征导纳； 为电导； 为电纳

指向原始笔记的链接

随后就能计算反射系数，

归一化阻抗导纳到反射系数的变换公式

为归一化阻抗； 为归一化导纳

指向原始笔记的链接

1.1.2. 史密斯圆图的类型

1.1.2.1. Z 图

Z 图由恒电阻圆、恒电抗圆和恒 圆构成。

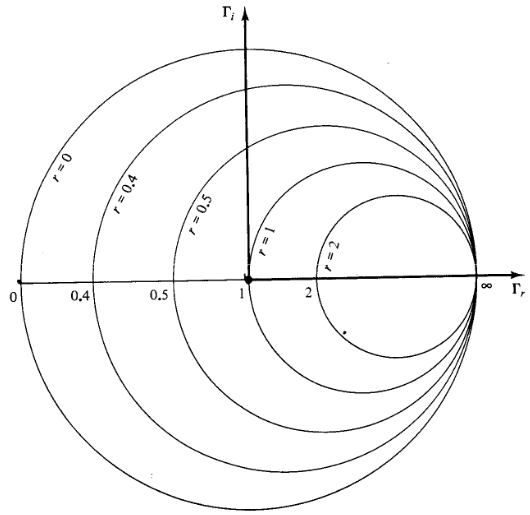阻抗圆圆心始终 轴，最右为开路，最左（最大圆）为短路。

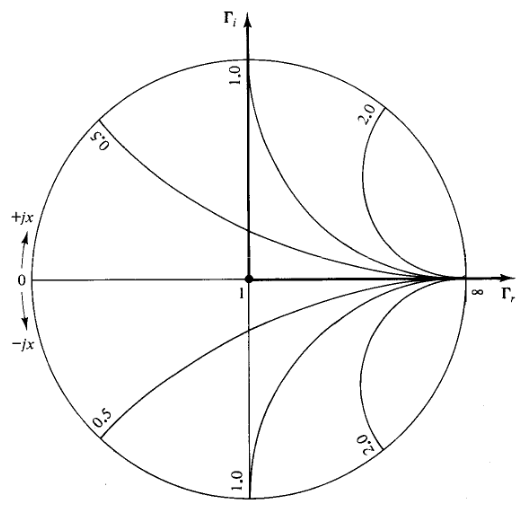恒电抗圆的圆心始终在 这条线上。需要注意的是，下半圆中的电抗圆的电抗值为负值。

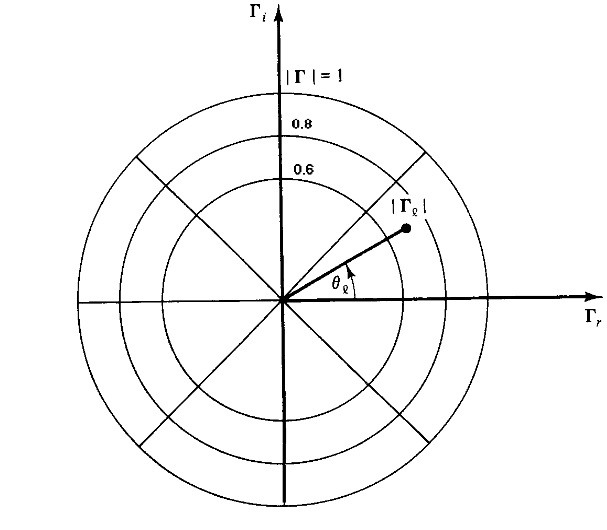这个图就是用极坐标表示的史密斯圆图了。可以看到始终有 。

把这三个图叠起来就是

我们实际上也能通过 Z 图来读出 Y。因为 Z 和 Y 在数学上互为倒数，当放在史密斯圆图中的时候，将 z 点沿着史密斯圆图的圆心对称（，欧拉恒等式），就能得到 Y 值。

1.1.2.2. Y 图

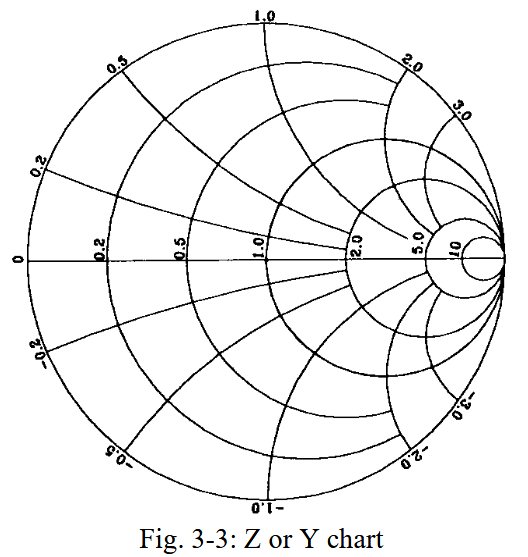
和阻抗图大致一样，只不过表示的含意变成了 而已，所以在使用的时候需要多加注意。

[! caution] 在考试画图时，需要标注好你使用的是 Z 图还是 Y 图。

[! important] 实际上，Y 图并不和 Z 图完全一样。就像前面说的一样，坐标轴固定的情况下， Z 图在旋转 之后才和 Y 图重叠。见旋转 Y 图。

1.1.2.3. 旋转 Y 图

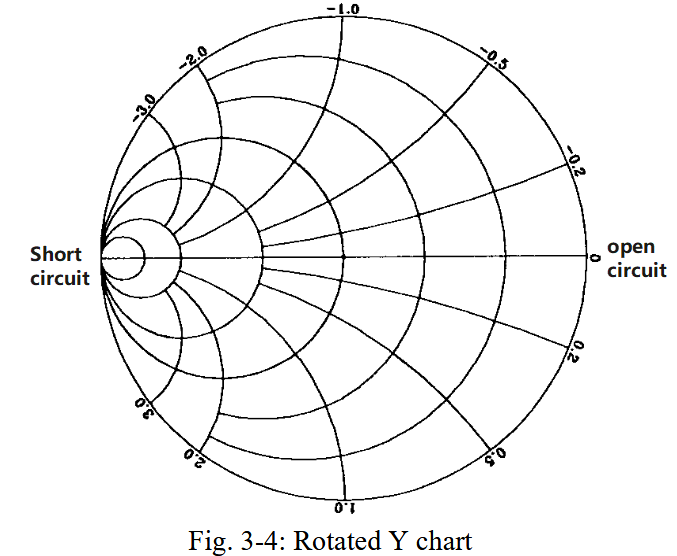
通过开路点和短路点能更好地看出 Z 图和 Y 图的中心对称性。

1.1.2.4. ZY 图

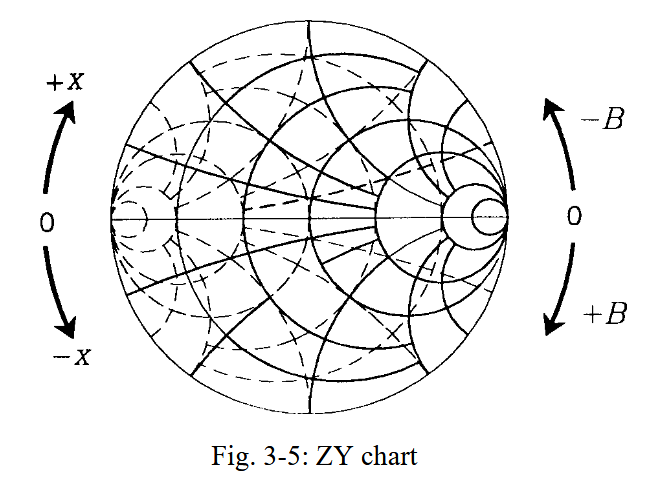
只有在相同坐标轴 的情况下，ZY 图才能一起使用。

在 ZY 图上的一点，可以同时读出 ， 和 。

[! note] 史密斯图适合快速、不要求精度的读数，作为计算的佐证。

1.1.2.5. 压缩（扩展）图

压缩（扩展）图包括正常的史密斯圆图（）加上额外的负电阻部分（），对于振荡器设计非常有用。

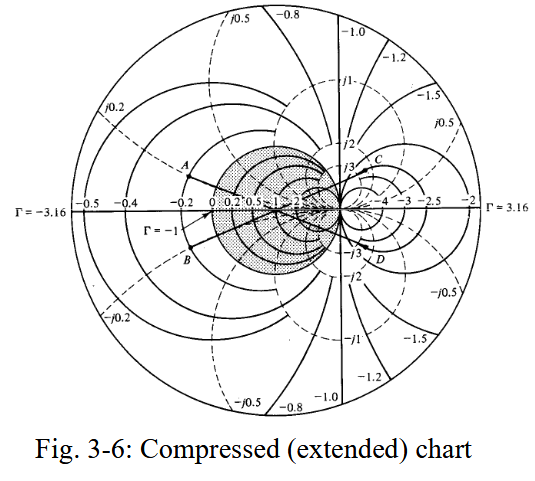
和史密斯圆图一样的读图方式。在对放大器的稳定性进行设计的时候，也会使用到这个图。

1.2. 无功器件对 ZY 史密斯圆图的影响

使用 LC 网络进行匹配的时候有以下规律

• 串联电感 L：增加电抗将导致负载沿着等电阻圆顺时针移动；
• 串联电容 C：减少电抗将导致负载沿着等电阻圆逆时针移动；
• 并联电感 L：减少电纳将导致负载沿着等电导圆逆时针移动;
• 并联电容 C：增加电纳将导致负载沿着等电导圆顺时针移动。

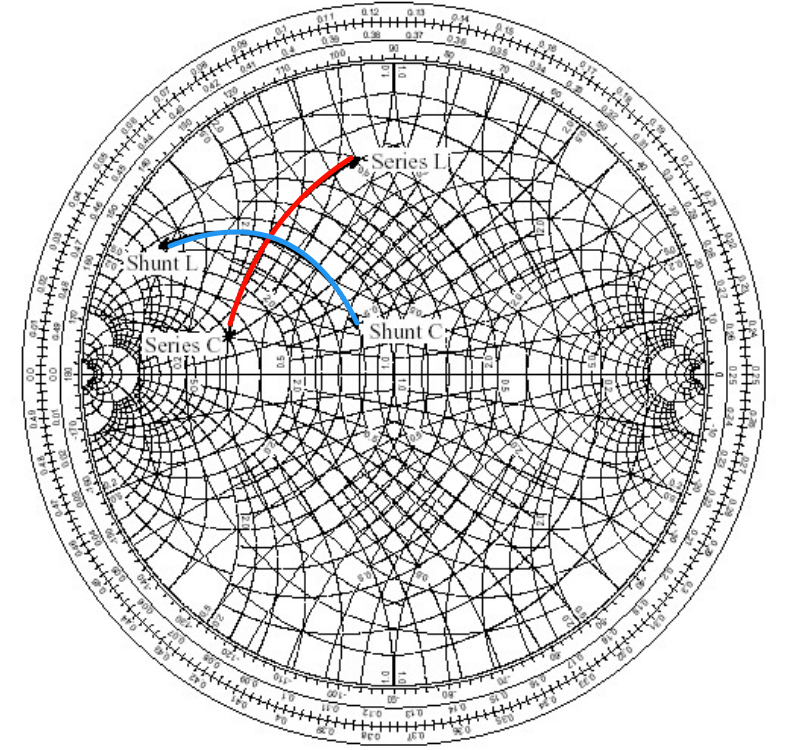
有个土方法 ，

• 串联顺着电阻圆移动，并联顺着电导圆移动
• 使用电感就是 Levitate（抬升），使用电容就是Crush（下降）

1.3. 使用史密斯图对网络进行阻抗匹配

1. 在史密斯圆图上绘制初始点（例如归一化负载阻抗）和最终点（例如源阻抗的复共轭）。
2. 沿着恒定电阻和电导圆画出弧线，将两个点连接在一起。
3. 读取每个电弧所需的归一化电抗或电纳值。
4. 确定给定频率下电感器和电容器的实际值。

Example 3-1

[! note] 一些拓展可见史密斯圆图的应用

2. 传输线阻抗匹配

2.1. 传输线对史密斯圆图的影响

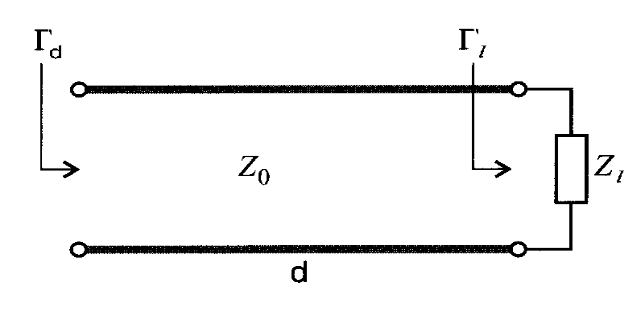
对于有 的负载 ，从长为 的传输线处向负载观察，此时的反射系数 为，

传输线距离d处反射系数计算式

指向原始笔记的链接

同样的，在距离阻抗距离 处有阻抗和导纳，

传输线向负载看去的输入阻抗计算式

为输入阻抗； 为反射系数；

指向原始笔记的链接

从这里可以看出，实际上串联传输线就是让原本的点沿着恒 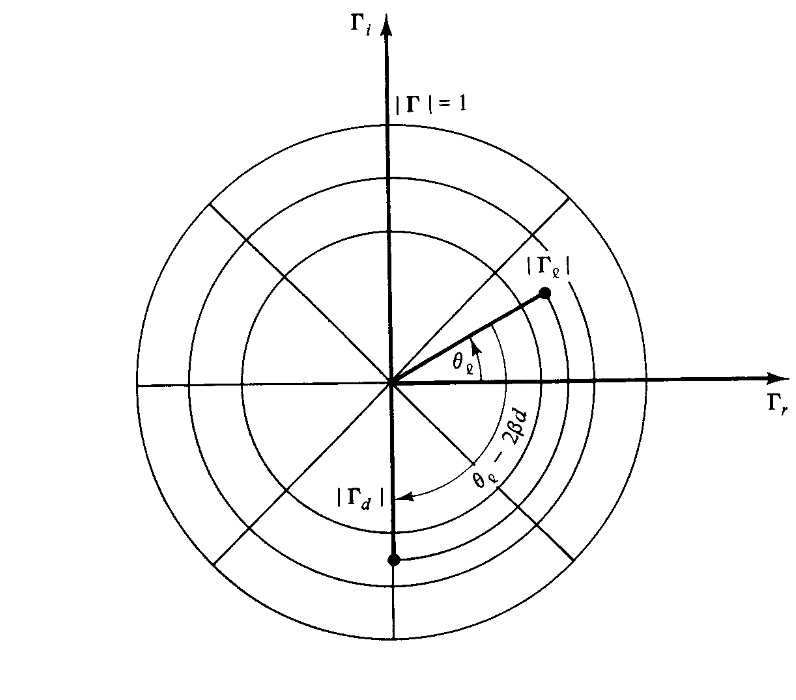圆顺时针移动了角度 ，也就是沿着源的方向移动，串联的传输线不会改变 值，仅仅会改变相位。

[! caution] 史密斯图中的源并不是实际电路中的源，而是指背离你观察方向的方向。

下面的不同的短截线，无论开路、短路都只是相当于改变了 ，也就是起始点的位置。然后短截线的长度

2.1.1. 短路短截线

如果短截线以短路的形式截断，在短路处则有 ，起始点在短路点。随后绕着电阻为 0 的圆，朝着源的方向行进。

2.1.2. 开路短截线

如果短截线以开路的形式截断，在开路处则有 ，起始点在开路点。

2.2. 单短截线匹配网络

短截线就是纯电感或者电容。

串联传输线与并联一个短路或开路短截线可以将 负载转换为任何导抗值，反之亦然。这里两段传输线的位置无所谓。

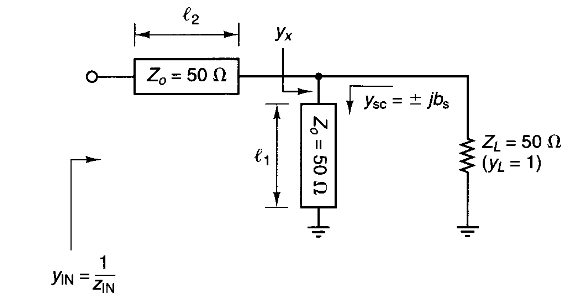
先来讨论并联的传输线。并联的传输线会增加电路的导纳，它既可以表现为电容，也可以表现为电感。对于电容性导纳，有 ；对于电感性导纳，有 。这里 的长度决定了 的值。

对于串联的传输线，其作用则是使得点沿着恒 圆朝着源的方向进行移动。

2.3. 四分之一波长变压器

四分之一波长变压器能让点沿着实轴 进行直线运动。有特征阻抗为 的四分之一波长变压器，它能让点从 圆横向移动到 圆。

2.4. 八分之一和八分之三波长短截线

这里相当于是固定了短截线的长度为八分之一和八分之三，然后去改变短截线的特征阻抗来实现设计。

2.5. 平衡短截线匹配网络

在实际实现中，单侧并联短截线通常被平衡短截线设计所取代，以最大限度地减少短截线和串联传输线之间的过渡相互作用。当然，并联短截线 ST1 和 ST2 的组合电纳必须等于单侧短截线所需的电纳。因此，平衡短截线每一侧的电纳等于单侧短截线的一半。然而，平衡短截线每侧的长度还不到单侧短截线的一半！