1. 无线通信滤波器
1.1. 滤波器规格
[! note] 这一部分是介绍可以用哪些参数来对滤波器的性能进行描述,
1.1.1. 插入损耗和功率损耗比
通常用插入损耗或者功率损耗比来表示滤波器的规格。
插入损耗计算式
指向原始笔记的链接
插入损耗 S21 定义式
指向原始笔记的链接
用 dB 表示的插入损耗
指向原始笔记的链接
为功率损耗比。
将传输的网络传输函数定义为,
网络传输函数定义式
指向原始笔记的链接
1.2. 低通滤波器的传输规格
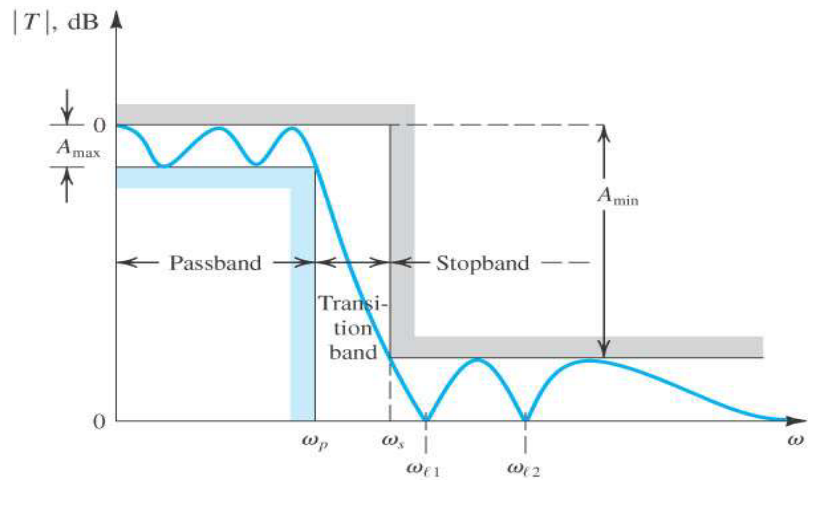
在低频的时候,信号接近 0dB。图中的
在高频的时候截止(信号很弱)。
在通带频率(
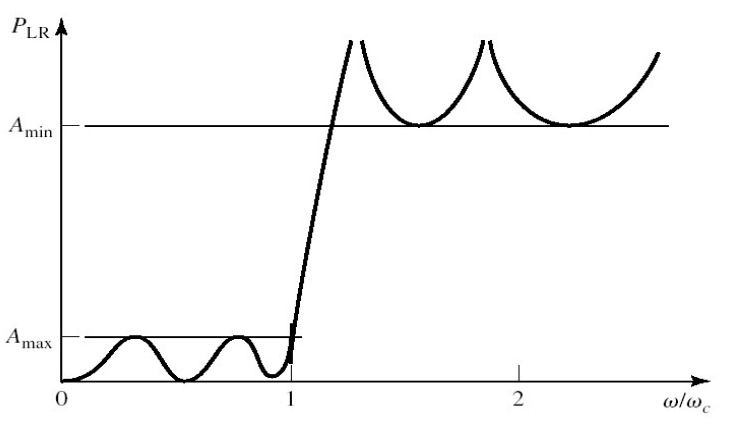
这一张损耗的图和增益图恰恰相反。
1.3. 带通滤波器的传输规格
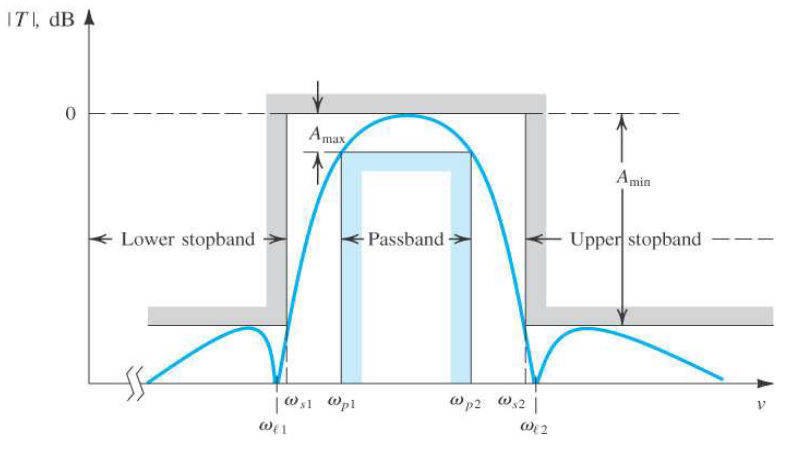
截止频率可以用算术平均或者几何平均,但是通常用后者。
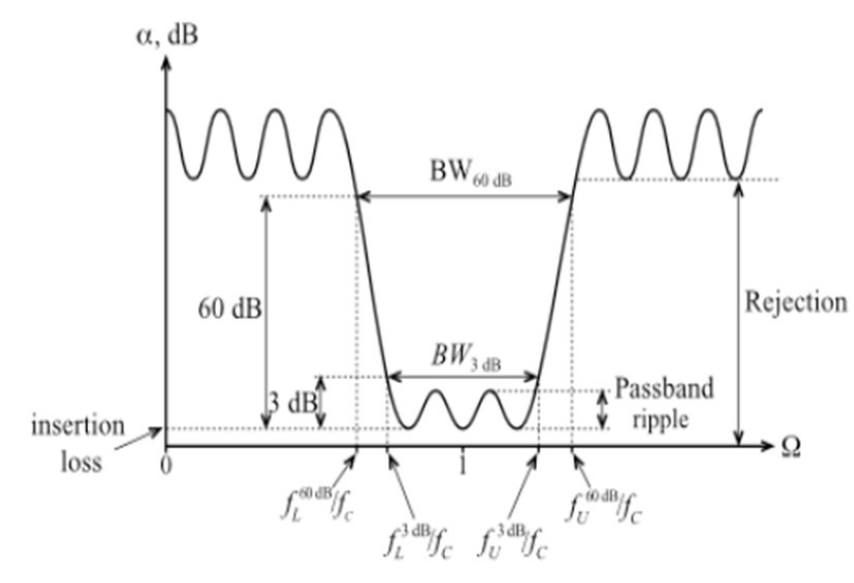
一般定义
2. 滤波器设计
最平坦响应
该特性也称为二项式或巴特沃斯响应。在给定的条件下,该响应能提供最平坦的通带响应。
对于低通滤波器它的插入损耗满足:
指向原始笔记的链接最平坦响应的插入损耗
指向原始笔记的链接
为滤波器的阶数; 是截止角频率。一般来说,设定在截止频率处,插入损耗为3dB,因此通常选择 。
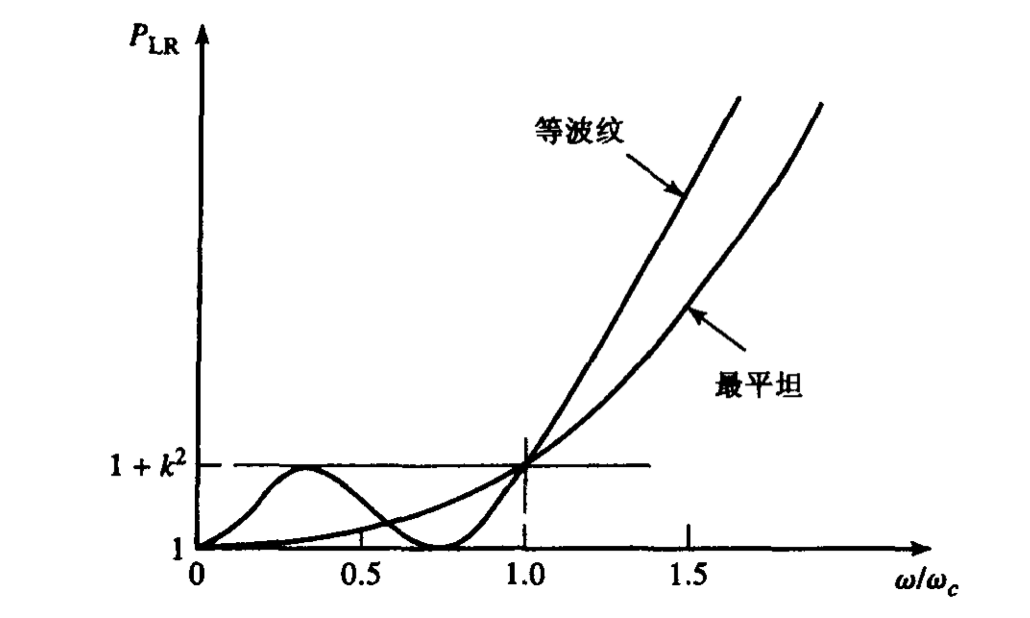
等纹波响应
若将切比雪夫多项式运用于 N 阶低通滤波器的插入损耗响应,则会得到陡峭的截止响应和幅度为
的纹波。 等纹波响应的插入损耗
指向原始笔记的链接
为滤波器的阶数; 是截止频率。一般来说,设定在截止频率处,插入损耗为 3dB,因此通常选择 。 该特性在通带内会有一个幅值为1+k2的波纹,不会像最平坦响应那样在通带内具有平坦的特性,但是等波纹特性的滤波器在截止频率处变化更陡峭,更接近理想低通滤波器特性。
指向原始笔记的链接
椭圆响应
椭圆响应在通带和阻带都会有纹波存在。
指向原始笔记的链接
如果最小插入损耗很重要,则可以使用最大平坦(巴特沃斯)响应。如果需要急剧截止,则等纹波(切比雪夫)响应更好。
2.1. 巴特沃斯滤波器的幅度响应
幅值平方函数的形式为,
巴特沃斯函数定义式
指向原始笔记的链接
为当前频率; 为滤波器截止频率
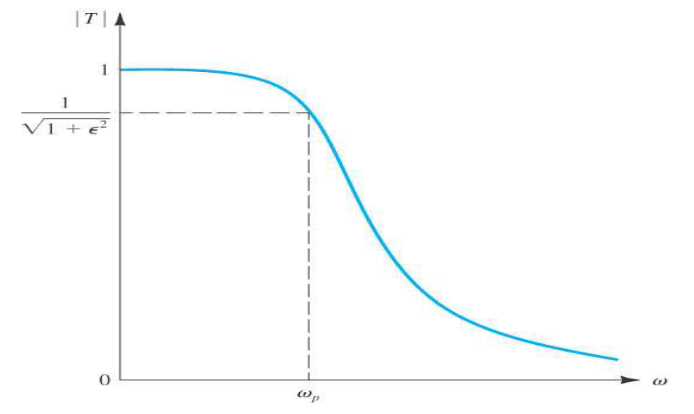
对于巴特沃斯响应,截止频率定义为
2.2. 切比雪夫滤波器的幅度响应
幅值平方函数的形式为,
切比雪夫函数定义式
指向原始笔记的链接
纹波计算式
指向原始笔记的链接
2.3. 通过插入损耗法设计原型滤波器
滤波器设计的插入损耗方法
插入损耗方法使用网络综合技术来设计具有完全指定的频率响应的滤波器。从阻抗和频率方面标准化的低通滤波器原型开始,设计得以简化。然后应用转换将原型设计转换为所需的频率范围和阻抗水平。
设计流程
插入损耗方法提供了分步方法:
指向原始笔记的链接
- 确定滤波器规格(截止频率、衰减、滚降)
- 设计低通原型(最大平坦、等纹波、椭圆、线性相位)
- 缩放和转换(频率、阻抗、元件类型)
- 使用适当的元件(LC、短截线、高阻抗低阻抗)实现
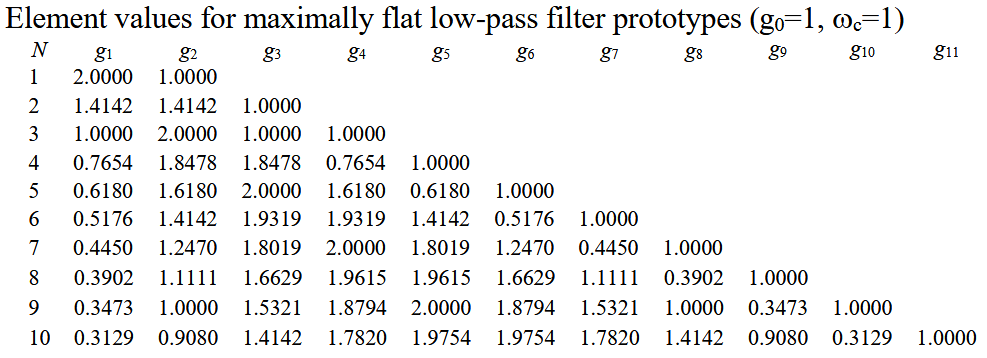
2.3.1. 最平坦低通滤波器原型设计
最平坦低通滤波器设计
对于归一化低通设计,其源阻抗是
,其截止频率为 ,并且 。由此构建的 N 阶梯形电路的元件值已经被制作成表格。
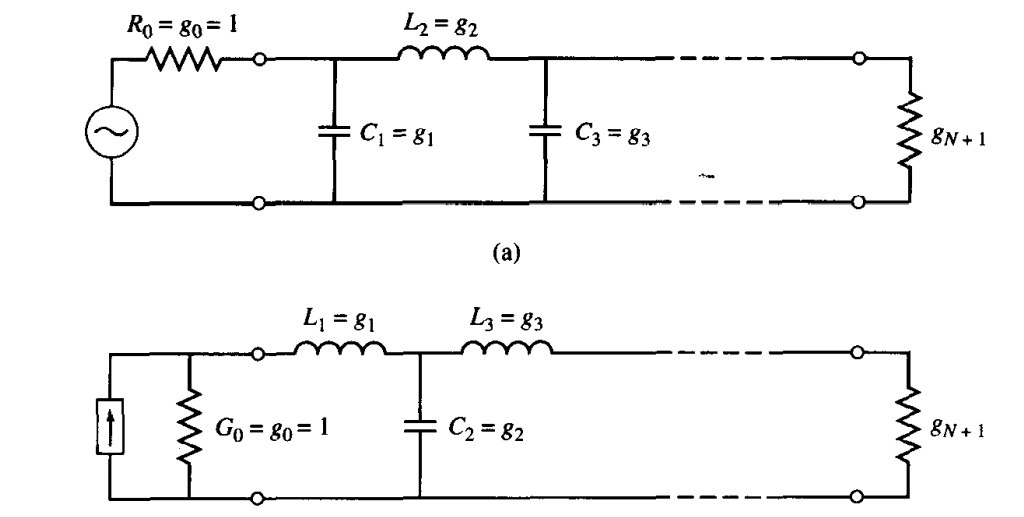
1. 电路选择
对于一个最平坦响应的低通滤波器,我们可以使用以下两种通用电路:
从信号源开始,我们可以选择第一个元器件为并联还是串联,之后的元件串并交替,两个电路均能够实现相应的功能。
第一个电抗性元件为电容的称为
(pi)型电路,第一个电抗性元件为电感的被称为 (tee)型电路。 Question
串并联之间有什么区别吗,会影响什么性能呢? 答:无区别,互为对偶,两者给出同样的响应。
对于有
个电抗性元件的滤波器,这些元件值已编号为从源阻抗 到负载阻抗 。这些元件在串联和并联之间交替出现,且 有下面的定义: 源 电 阻 源 电 导 到 串 联 电 感 器 的 电 感 并 联 电 容 器 的 电 容 负 载 电 阻 , 若 是 并 联 电 容 负 载 电 导 , 若 是 串 联 电 感 于是,上图所示的两种电路就可以认为是互为对偶的,两者给出同样的响应。
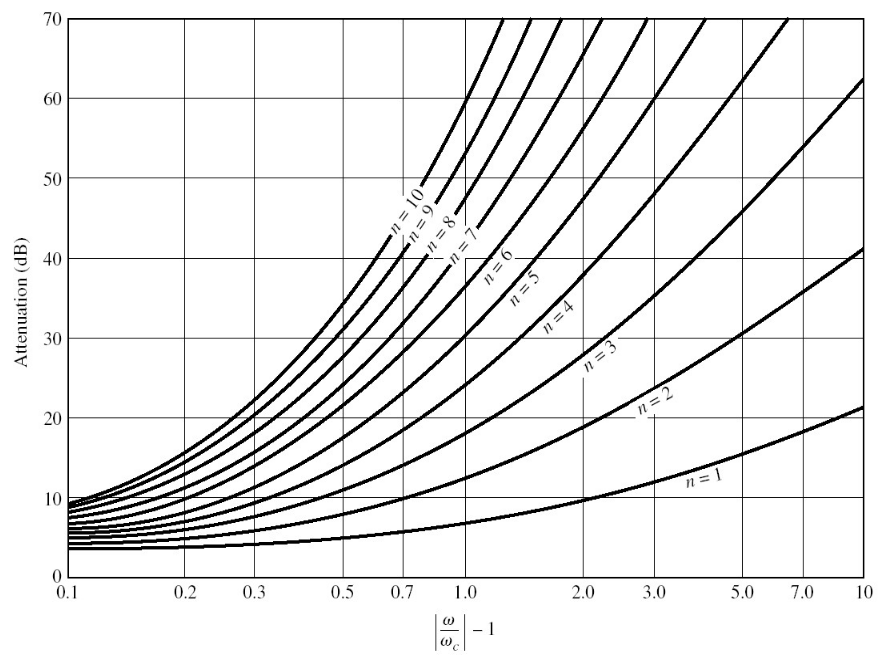
2. 阶数确定
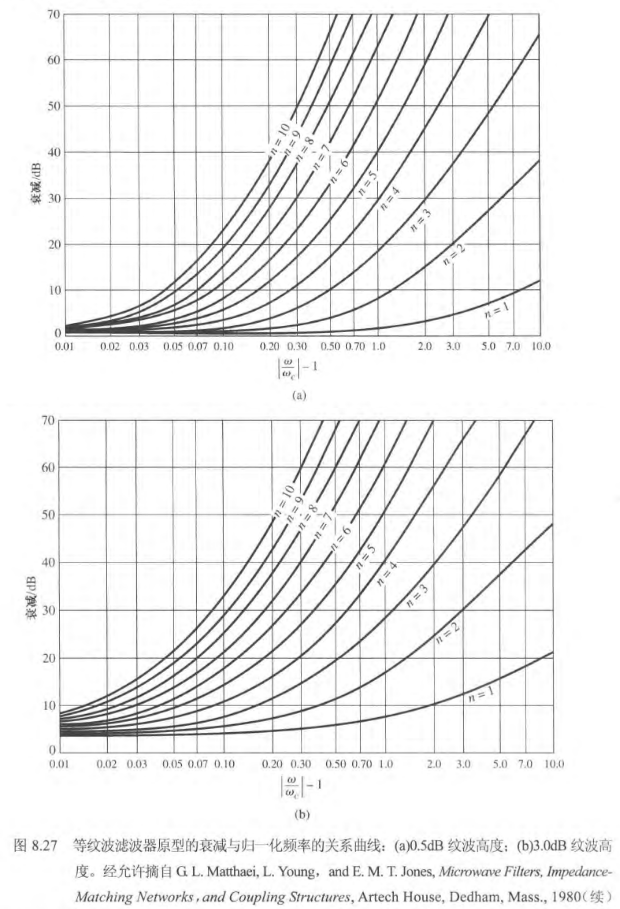
给定固定频率时的插入损耗值,我们可以根据下表确定滤波器的阶数:
一般题目会给出要求,例如“在 2GHz 时插入损耗至少为30dB”,题干中又给出截止频率为 1GHz,这里
指向原始笔记的链接,再减去 1 之后就等于 1。如果想达到 的衰减,按照曲线而言则至少需要 5 阶。5 阶就意味着需要 5 个集总元件。
2.3.2. 等纹波低通滤波器原型设计
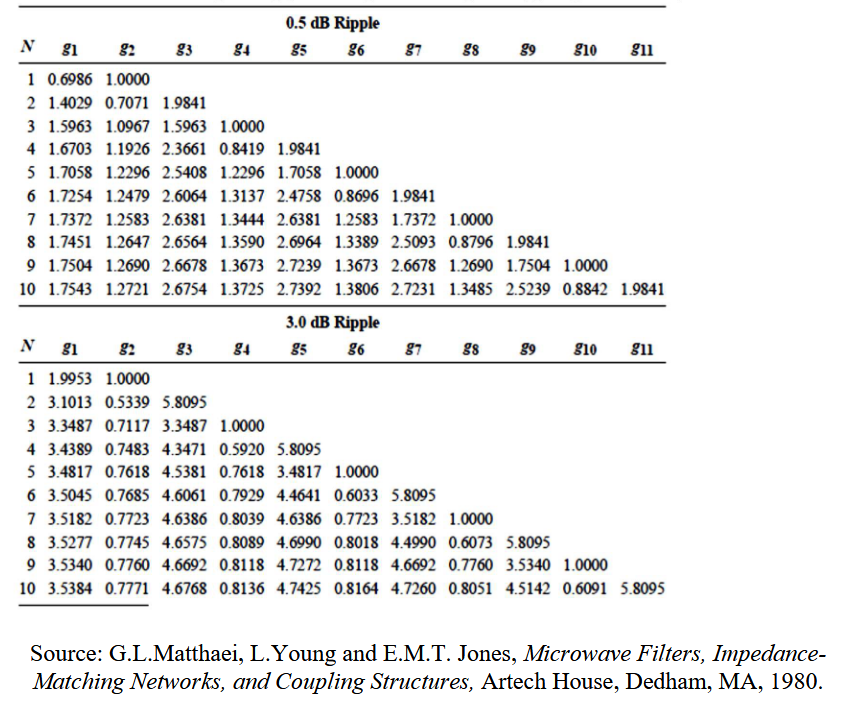
等纹波低通滤波器设计
对于归一化低通设计,其源阻抗是
,其截止频率为 ,并且 。由此构建的 N 阶梯形电路的元件值已经被制作成表格。 [! attention] 注意,负载阻抗对于偶数
有 。 等纹波滤波器一般分为两种:带内纹波为 3dB 和带内纹波为 0.5dB。
电路结构
电路基本结构和 最平坦低通滤波器原型设计 是一样的。
确定滤波器阶数
通过下图,我们可以知道多少阶的滤波器可以满足我们的需求。
确定阶数之后,即可在「等纹波低通滤波器原型的元件值」表中查找原型器件值。
指向原始笔记的链接
2.4. 滤波器阶数
对于巴特沃斯多项式而言,有
巴特沃斯多项式通带最大损耗计算式
指向原始笔记的链接
巴特沃斯多项式阻带最小损耗计算式
指向原始笔记的链接
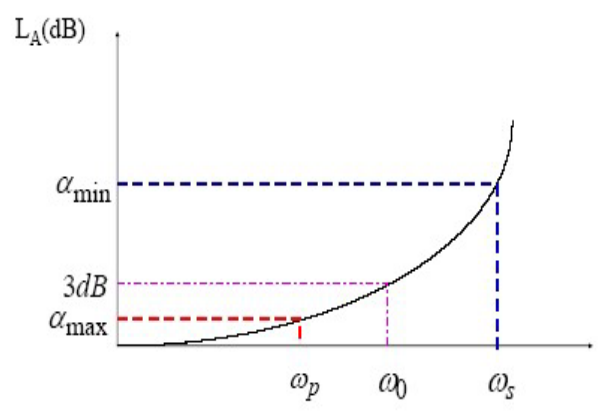
对于通带,
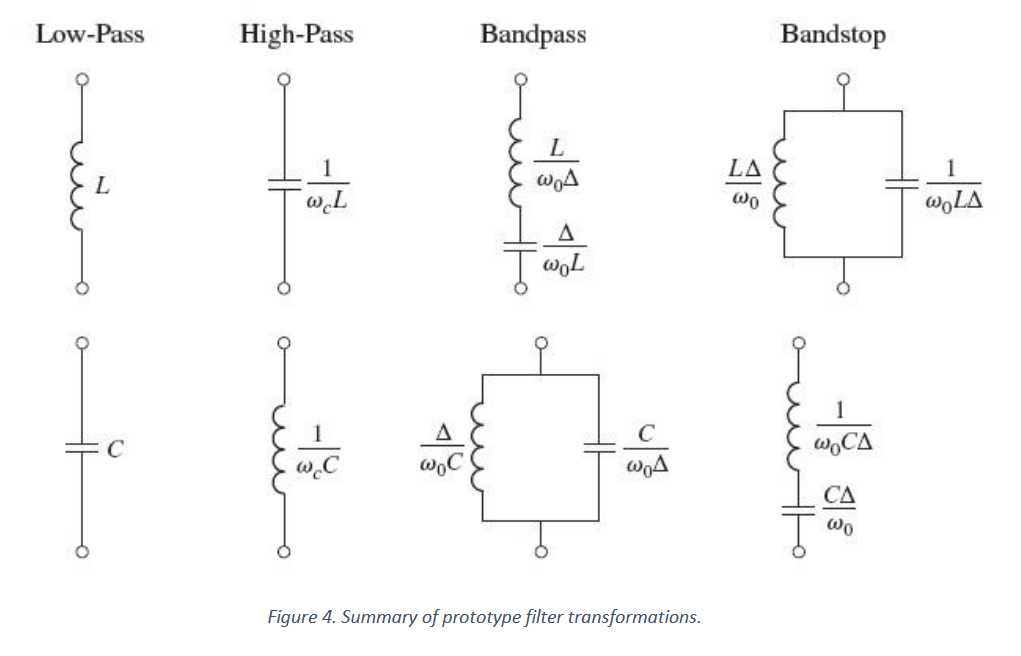
3. 滤波器变换
滤波器转换
原型低通滤波器原型是一种归一化设计,假设了源阻抗为
,截止频率为 。需要在阻抗和频率方面扩展这些设计,并进行转换才能提供高通、带通或带阻滤波器特性。 阻抗缩放
在原型设计中,源电阻和负载电阻是统一的。唯一的例外是具有偶数阶的切比雪夫滤波器,其负载电阻具有非单位值。如果源电阻不是 1 而是
,则原型电路的所有阻抗都应乘以 。如果我们使用素数来表示缩放后的分量值,则新的滤波器分量由下式给出 其中 L、C 和 RL 是原始低通原型的元件值。
频率缩放
低通到低通
确定缩放因子:
,所有元器件值乘以这个缩放因子即可。 低通到高通
我们使用以下频率替换将低通响应转换为高通响应,
低通到带通
低通原型滤波器设计可以转换为具有图 3 所示的带通或带阻响应。如果
和 表示通带的边缘,则可以使用以下频率替换获得带通响应, 总结
指向原始笔记的链接
4. 滤波器实现
在设计完原型低通滤波器之后,我们通过滤波器变换得到了滤波器原型。在微波尺度上,我们需要使用分布式元件去替代集总元件。
接下来,会用 Richard 变换和 Kuroda 恒等变换
4.1. Richard 变换
Richard 变换
指向原始笔记的链接
4.2. Kuroda 恒等变换
Kuroda 恒等变换
指向原始笔记的链接
5. 阶梯式阻抗低通滤波器
2024-08-28 P25
6. 阻抗和导纳逆变器
逆变器定义为一个二端口网络,能根据以下关系将终端阻抗
类似的,有参描述导纳逆变器的特征参数
[! note] 在 1 端口电路中,阻抗
、导纳 和反射系数 描述的是同一个东西,都是端口的电流电压之间的关系。在 2 端口网络中,我们就用 S 参数、ABCD 参数以及 G、H 参数来对端口的电流电压关系进行描述。
通过引入一端长
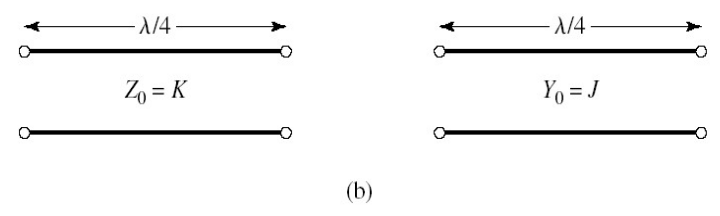
逆变器可用于将并联元件转换为串联元件,反之亦然。
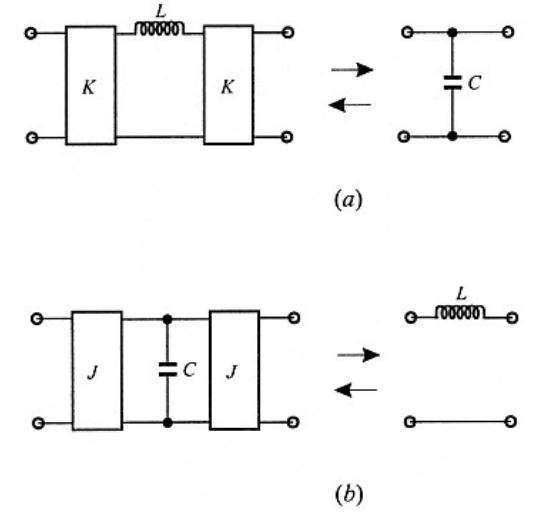
[! tip] 用 ABCD 参数
通过负元件去更改其他元件的值。
7. 耦合线滤波器
可以使用包括
对于单段开路耦合线,

对于单端开路耦合线,实际上只能当作 2 端口网络来进行分析,因为有两个端口是开路的。于是有 ABCD 参数,
现在考虑由 N+1 个耦合线部分组成的带通滤波器:
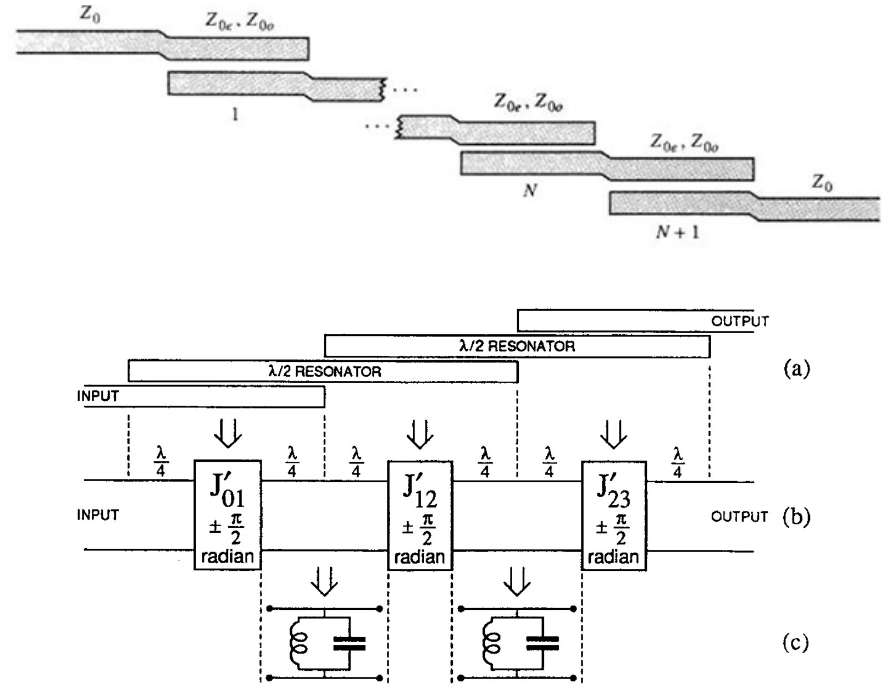
LC 谐振器(resonator)
自谐振频率计算公式
指向原始笔记的链接
电感值; 电容值。
S 2.7 Coupled Line Filters Examples
8. 耦合谐振器滤波器
8.1. 使用四分之一波长谐振器的带阻和带通滤波器
这些结果仅适用于具有相同输入和输出阻抗