用功率损耗比表征滤波器响应

1. 表征方法

1.1. 用功率损耗比表征

在插入损耗法中，无损滤波器的响应由滤波器的功率损耗比来定义：

插入损耗计算式

指向原始笔记的链接

1.2. 用插入损耗表征

用 表示的插入损耗为：

用 dB 表示的插入损耗

为功率损耗比。

指向原始笔记的链接

1.3. 用 S21 表征

我们还可以用 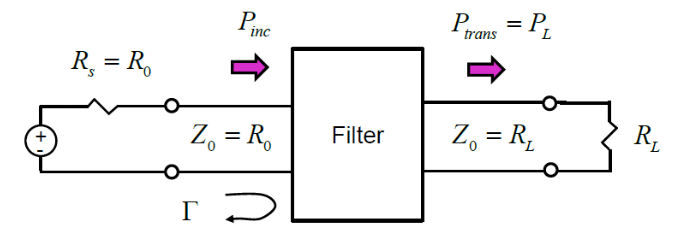来定义插入损耗。如果该网络的负载端口和源端口均匹配，则有：

插入损耗 S21 定义式

指向原始笔记的链接

用 来表示就是，

如果滤波器是无损的，则能量转换：

1.4. 用反射系数表征

由于 是 的偶函数，它可以表示为 的多项式，因此可以将其变换为，

其中， 和 是 的实数多项式。代入功率损耗比定义式即可得到，

用反射系数幅度计算的功率损耗比

和 是 的实数多项式。

指向原始笔记的链接

注意，指定功率损耗比的同时也限制了反射系数的幅度 。

2. 最平坦响应的表征

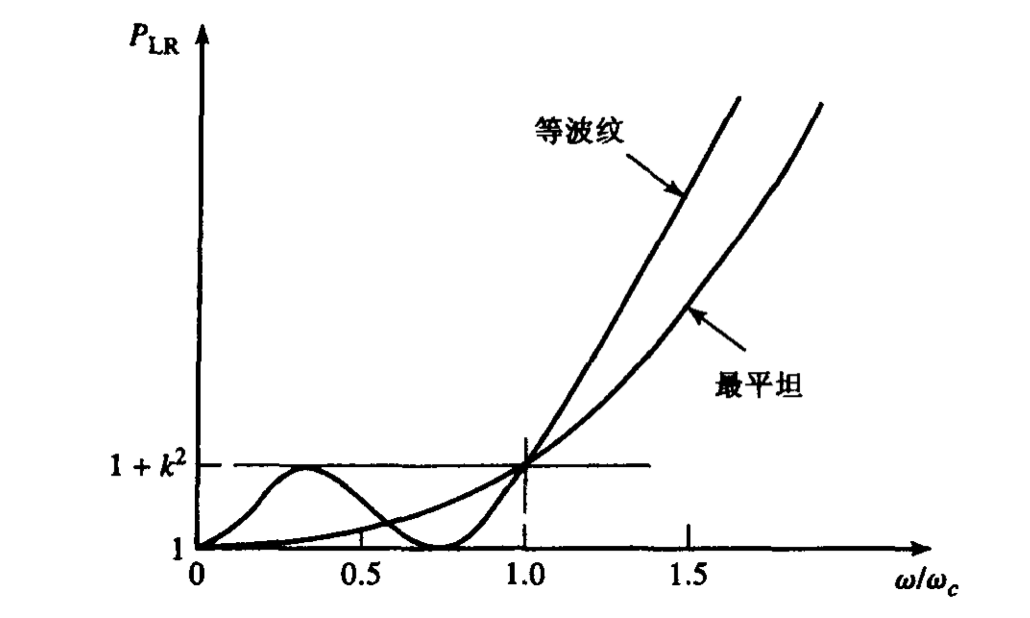
最平坦响应

该特性也称为二项式或巴特沃斯响应。在给定的条件下，该响应能提供最平坦的通带响应。

对于低通滤波器它的插入损耗满足：

最平坦响应的插入损耗

为滤波器的阶数； 是截止角频率。一般来说，设定在截止频率处，插入损耗为3dB，因此通常选择 。

指向原始笔记的链接

指向原始笔记的链接

3. 等纹波响应的表征

等纹波响应

若将切比雪夫多项式运用于 N 阶低通滤波器的插入损耗响应，则会得到陡峭的截止响应和幅度为 的纹波。

等纹波响应的插入损耗

为滤波器的阶数； 是截止频率。一般来说，设定在截止频率处，插入损耗为 3dB，因此通常选择 。

指向原始笔记的链接

该特性在通带内会有一个幅值为1+k2的波纹，不会像最平坦响应那样在通带内具有平坦的特性，但是等波纹特性的滤波器在截止频率处变化更陡峭，更接近理想低通滤波器特性。

指向原始笔记的链接