电阻中的电子处于不断随机运动的状态意味着随机变化的电流流过整个电阻,电阻两端的电压随时间变化的随机性
热运动。 更热 ⇒ 电子移动更多 → 更大的电压
热噪声在 0K 时为零,所以永远不会是零
因为是随机电压,所以用统计学来描述。
-
大量的电子在移动 (
/ , in a resistor) -
移动速度非常快(
碰撞/秒/电子)。
无论何时测量,噪声看起来都是一样的 (对于恒定的温度、带宽等) (“统计学上的静止”)。用时间来描述平均数
噪声电压可能为正、负或者 0。因此我们测量 RMS(均方根)电压。
电压峰值一般为均方根电压的三倍。
频谱
在所有有用的频率上都会产生热噪声
如果用相同的带宽测量,热噪声在所有频率
Keypoint
RMS 热噪声确实取决于所使用的带宽
振幅 x0.5 如果带宽 x0.25(统计!)
带通滤波有同样的效果(注意平均频率是一样的,但窄带宽的信号更加连贯)。
基本噪声运算
热噪声总是以电压源串联电阻的形式出现。我们可以用奈奎斯特公式来对它进行描述。
奈奎斯特公式
指向原始笔记的链接
为热噪声(V); 为玻尔兹曼常数;T 为开尔文温度(K);R 为电阻值( );B 为带宽(Hz)。
有用的经验法则
60
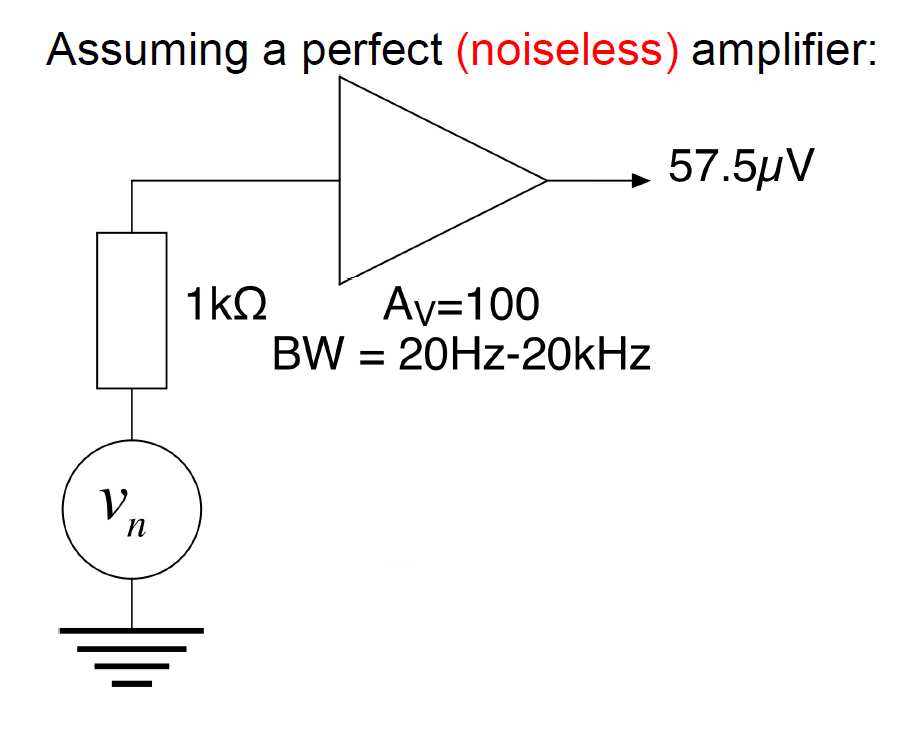
@300K 1nV ,可以用此来快速估算
热噪声的大小与频率并不相关,只和选择的带宽相关。
电压噪声频谱密度
指向原始笔记的链接
为热噪声频谱密度( ); 为玻尔兹曼常数;T 为开尔文温度(K);R 为电阻值( );B 为带宽(Hz)。
电流噪声频谱密度公式
指向原始笔记的链接
为电流噪声频谱密度( ); 为玻尔兹曼常数;T 为开尔文温度(K);R 为电阻值( );B 为带宽(Hz)。
根据上面的公式我们可以看出:
- 噪声随着带宽上升而增加
- 电压噪声随着电阻增加而增加
- 电流噪声随着电阻增加而减少
热噪声模型
噪声电压和噪声电流和一般电压电流具有一样的性质。
多噪声源
噪声串联
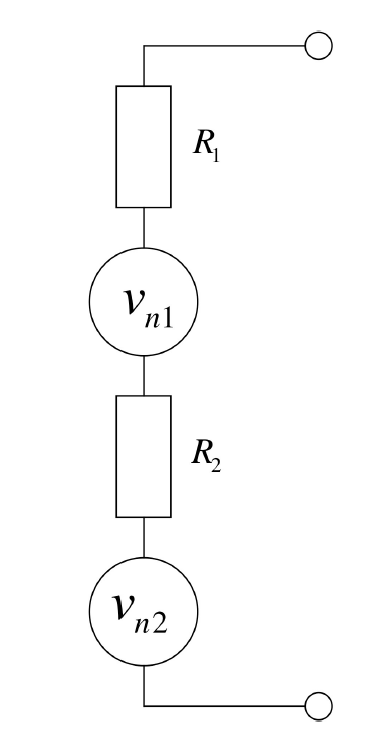
噪声电压之间是不相关的,两个噪声可能相反或者相同。因此使用平均噪声功率和:
均方根电压的平方和再开方
噪声并联

此时我们通过叠加定理和分压定理可以计算出输出的总噪声