1. 数字系统中的数据通路
一般数字系统由以下几个部分构成，数据通路、控制模块、存储模块和互连网络。
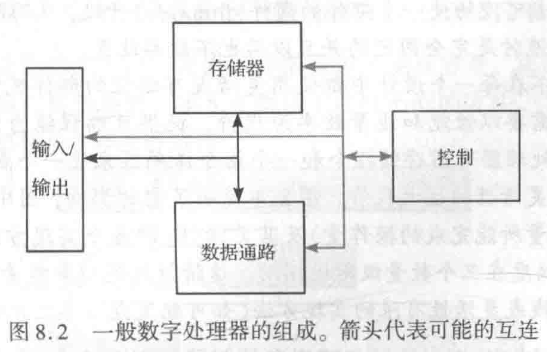
数据通路是系统的核心，其负责所有的计算。结果存储在存储模块。
存储模块寄存器用于存储可以同时访问的各个数据
互连模块则是将其他所有模块相连接。互连可以采用不同的样式，例如总线或网状互连（点对点）。总线能连接很多模块，但是同时只有一个模块能写总线（但是能同时读总线上的数据）。连接到总线的所有模块的输出都需要三态缓冲器。
数字系统中的数据通路主要由算术模块组成，常见的算术模块包括加法器（减法器）、乘法器、移位器。
2. 算术模块
2.1. 移位器
组合移位器对于算术运算非常有用，因为移位相当于乘以 2 的幂。移位寄存器更简单但是每个时钟周期只能移动 1 位。
固定方向和位数的简单移位可以通过硬件重新布线轻松实现。这里主要学习移位器：硬连线移位器、可编程移位器、桶形移位器、对数移位器
2.1.1. 硬连线移位器
硬连线移位器很好理解。硬连线移位器只能用来移动固定位数。
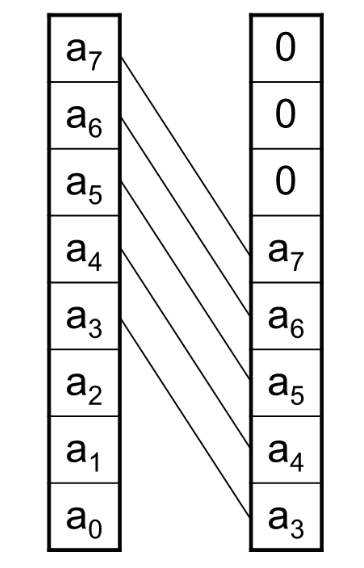
2.1.2. 可编程移位器
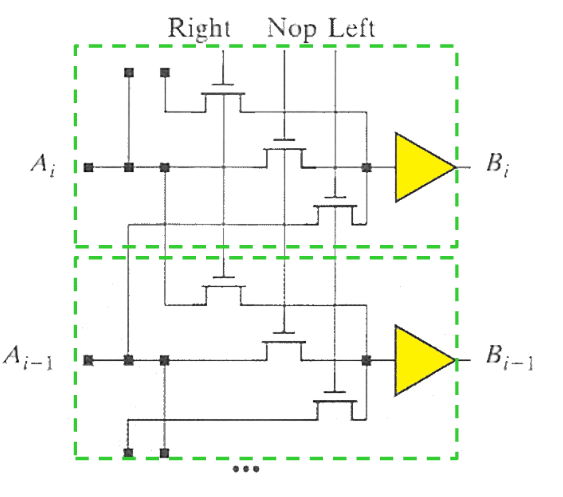
1位左右移位器能用于向左或者向右移位 1 位。用于控制的输入同时只能有一个为“1”。
2.1.3. 桶式移位器
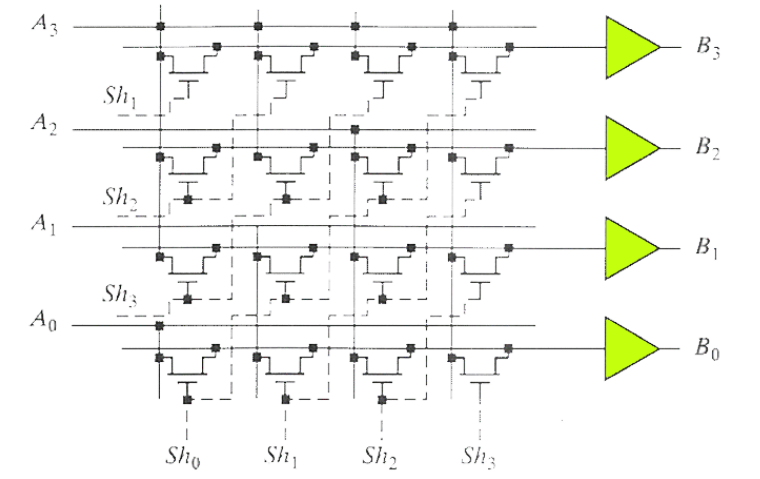
桶形移位器的行数为字长，列数为最大的移位宽度。
同样控制输入只能同时有一个为“1”。当
其优点在于信号只通过 1 个传输门，因此延迟对于任何移位都是恒定的。控制信号通常需要解码器（n 个信号）。
缺点在于移动方向固定。（或许能通过使用更多的晶体管来让他左移？）
2.1.4. 左旋转线性桶形移位器
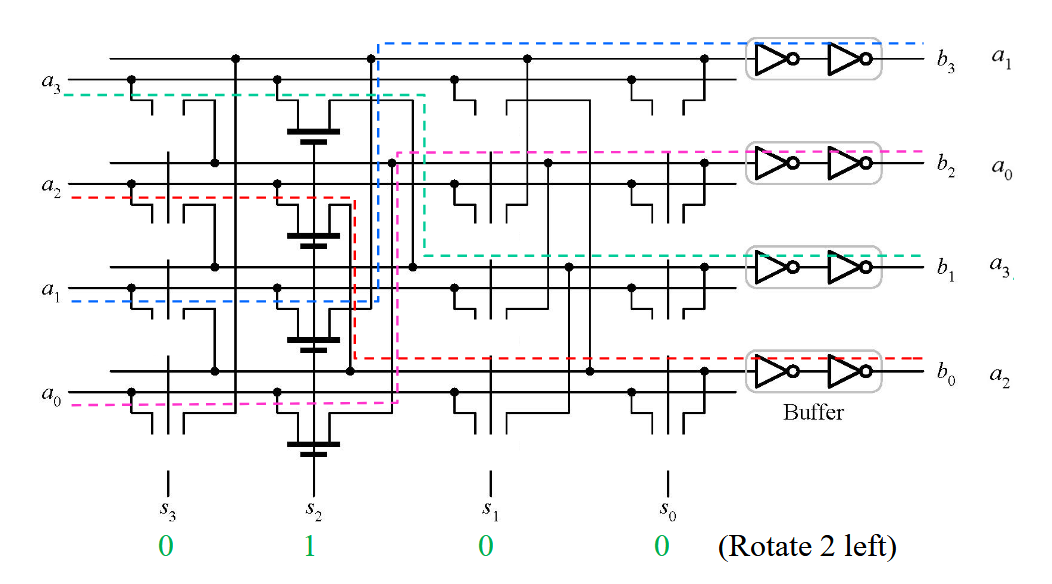这是桶形移位器的一个特殊形式，旋转意味着 LSB 不会丢失，而是会被补充到 MSB。左移就是这里的下移。
2.1.5. 对数移位器
通过三阶电路结构，能够实现从 0~7 位的移位。
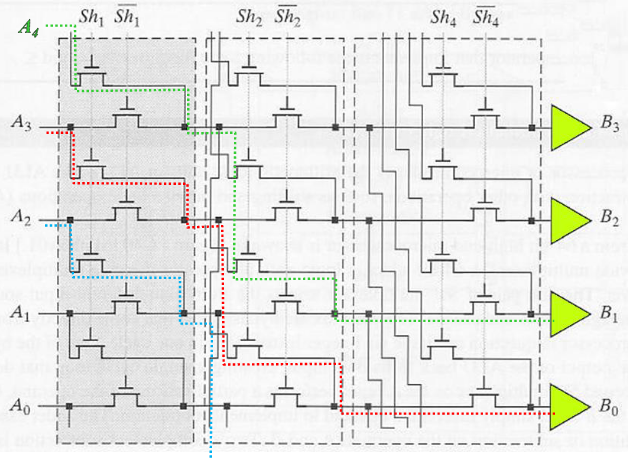演示了
对数移位器的优点在于，
- 控制信号采用编码形式，因此控制信号较少
- 不需要解码器
- 对于大移位值比桶形移位器更有效
- 比桶形移位器面积更小，速度更快
2.2. 加法器
加法是最常用的算术运算。它通常也是限速元件（性能瓶颈）。加法器的优化非常重要，优化可以在逻辑（逻辑门）或电路（晶体管）级别进行优化。逻辑级别优化尝试重新排列布尔方程，以便实现更快和/或更小的电路。电路优化控制晶体管尺寸和电路拓扑以优化速度
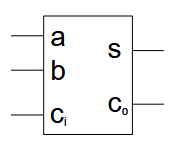
2.2.1. 全加器
全加器
将两个对应位的加数和来自低位的进位 3 个数相加，并输出一个和以及一个进位。这种运算称为全加，所用的电路称为全加器。
有逻辑式为，
指向原始笔记的链接
2.2.2. 纹波进位加法器
将 n个全加器的进位和出位相连接来构造一个 n 位加法器。进位很慢，需要优化进位的速度。
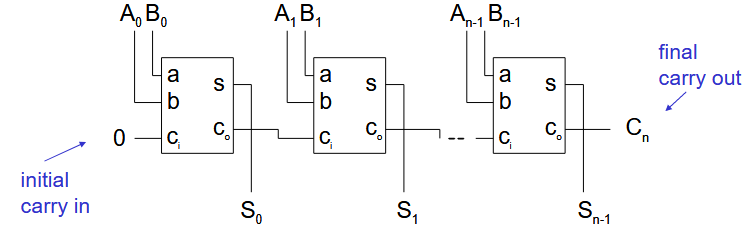
2.2.2.1. 纹波进位加法器的延迟
对于 n 位纹波进位加法器，最坏情况的延迟是 LSB 生成的进位一直传播到 MSB。此时有延迟，
从延迟方程可知，关键路径位于进位链上。
2.2.2.2. 加法器的反相特性
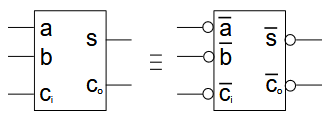
加法器的反相特性是指，当全部输入反相的时候，全部输出也反相。
2.2.3. CMOS 全加器
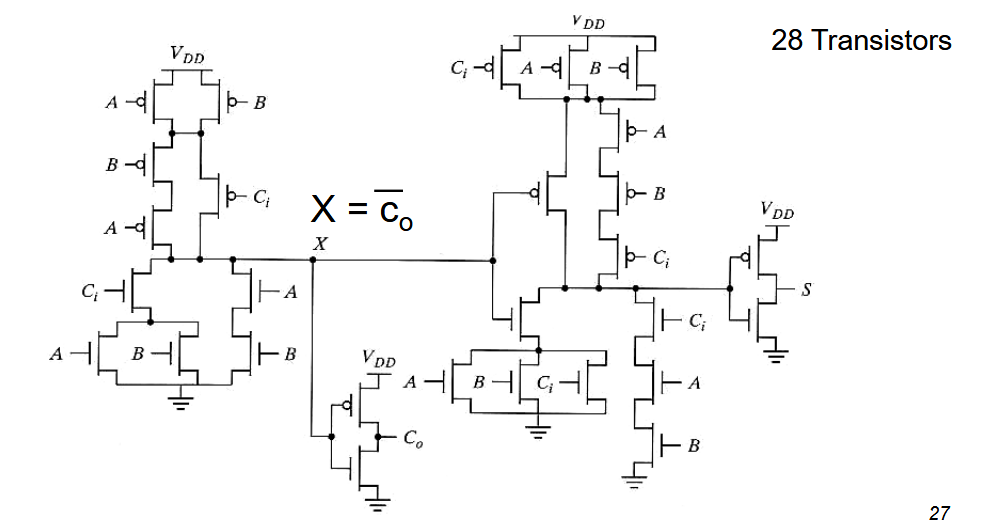
互补静态 CMOS 全加器的缺点：
- 单元有 28 个晶体管
- 大而慢的
- PMOS 堆栈位于进位和求和部分
- co 的固有电容很大：6 个栅极 + 2 个扩散 + 互连电容，需要驱动很多晶体管
- 进位通过 2 个反相级传播
- 求和输出需要额外的逻辑（虽然并不重要）总共使用了 28 个晶体管来实现。
2.2.3.1. 一些改进
移除进位链的反相器。
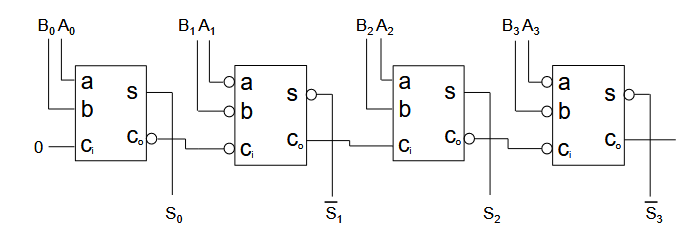（但是这样输入不是会增加反相器？）
2.2.4. 基于传输门（Transmission–Gate）的加法器
定义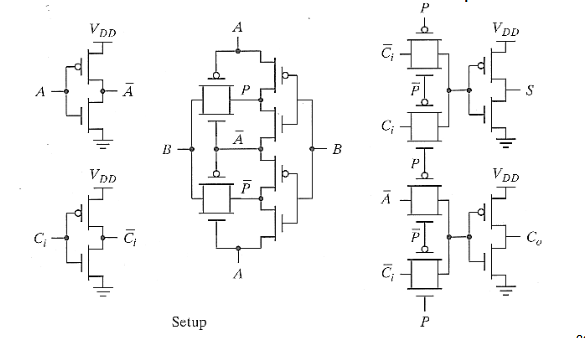 
上面的电路展示了如何得到
2.2.5. 曼彻斯特进位门
进位门能进一步简化，
D 的含意就是，当 A 和 B 同时为 0 的时候，进位为多少都无所谓，不会有 carry out。同理，P 就是用来传播进位，G 用来产生进位。
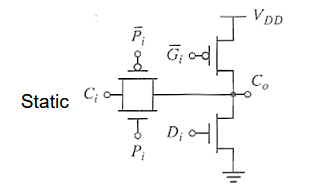
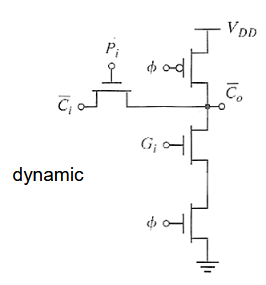我们可以先看真值表。进位会被 P 或者 G 和 D 控制，要么就是 P 控制直接将进位传过去，要么就是 P 不传进位，由 G 产生或者 D 删除进位。
| A | B | P | G | D | ||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| 右图是动态电路的版本， | ||||||
 |
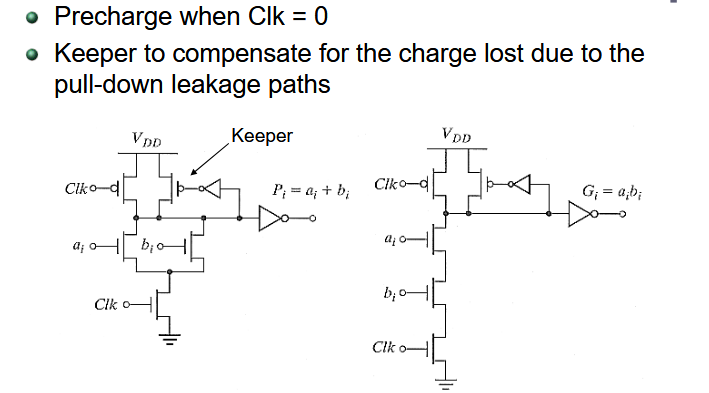2.2.6. 4-bit 曼彻斯特进位链
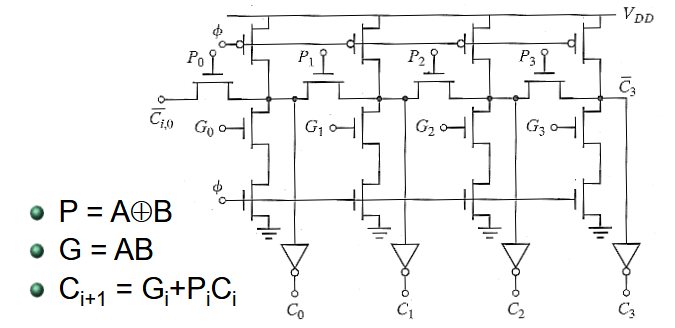曼彻斯特进位链是用传输门构建，并且预充电为
2.2.7. 进位旁路加法器
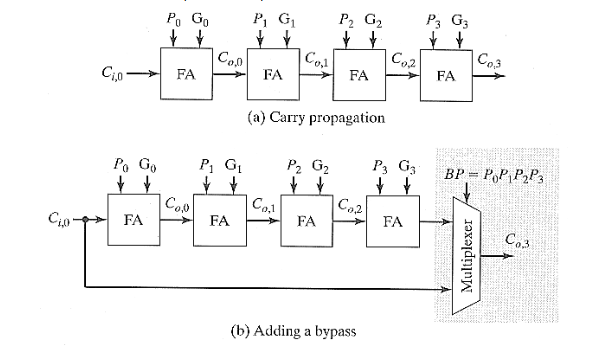当
如果有 N-bit 的加法器，可以分为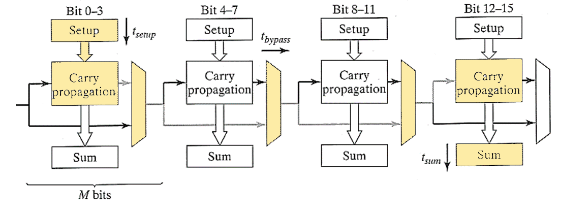 
总最长延时为
= fixed delay to get P and G signal = carry delay in 1 bit, worse is M bit in 1 stage = delay through MUX in 1 stage = delay of sum in final stage
（
2.2.8. 进位选择加法器
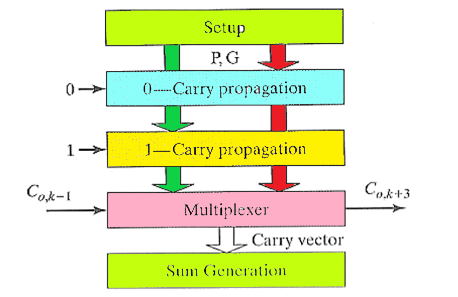这个的思想和动态电路一样，就是提前将两个结果都计算出来，然后后面的进位来的时候，根据进位进行结果的选择。
2.2.9. 线性进位选择加法器
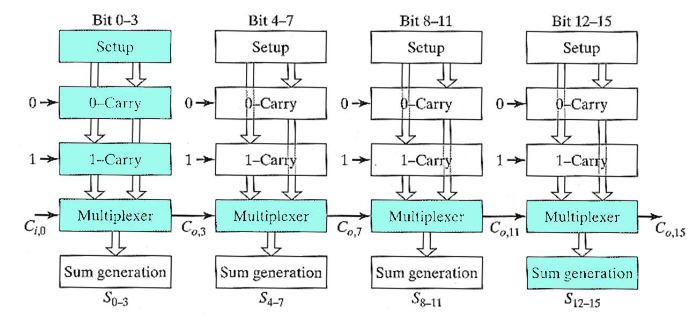N 位加法器内置 M 位进位选择，划分成
2.2.10. N 位平方根进位选择加法器
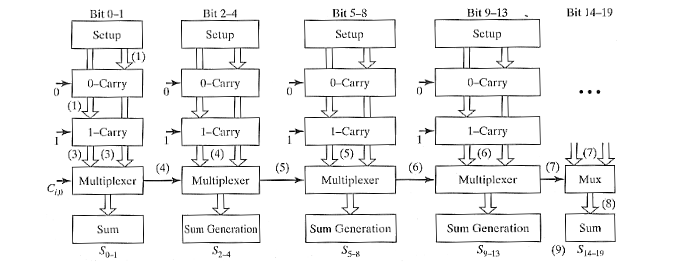在线性进位选择加法器的基础上，通过增加每一阶的位数，使得第一阶最快，最后一阶最慢。这里举例是，第一阶只处理 2 位，后面每一阶多处理 1 位，总阶数约为
2.2.11. 超前进位加法器 (CLA)
超前进位加法的思想是通过增加额外逻辑来消除进位引起的延迟。利用下面的公式就能算出第 n 个进位，
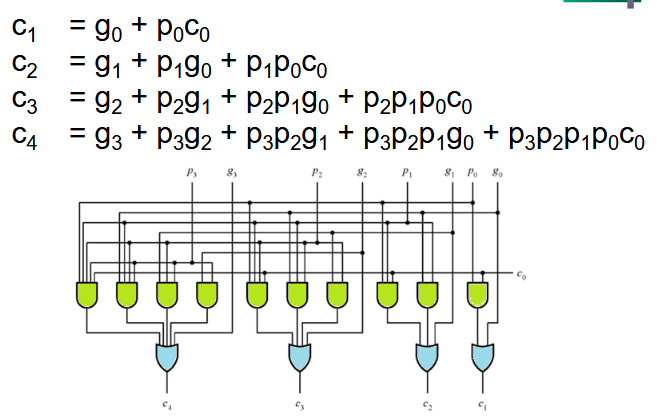
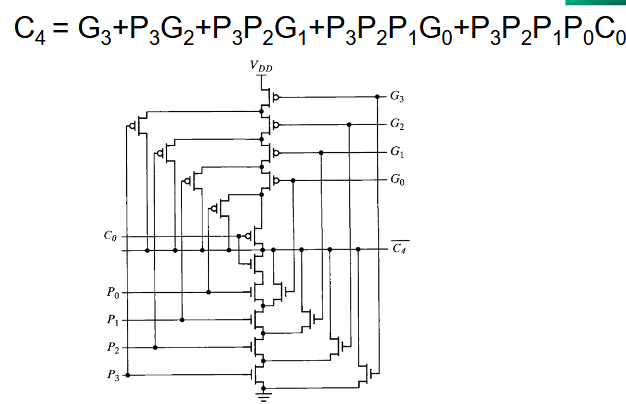
2.2.11.1. 4 位超前进位加法器
这里给出一种从
2.3. 乘法器
2.3.1. 二进制乘法
考虑两个没有符号的二进制数
其中有，
然后复习一下小学概念，被乘数和乘数，以及部分积和结果。
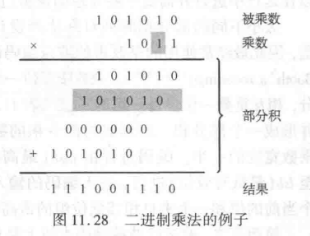这里需要注意，每一行部分积都是乘数和被乘数相与的结果。我们可以用点图来表示部分乘积。
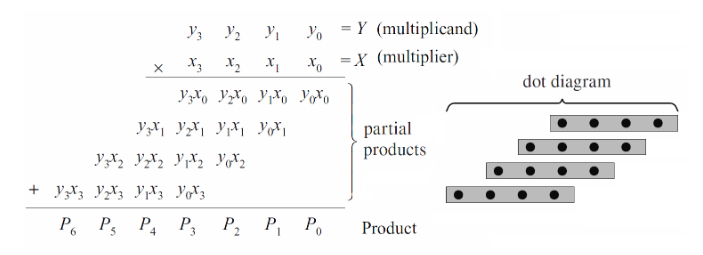点积都能用逻辑“与”来实现，下图中的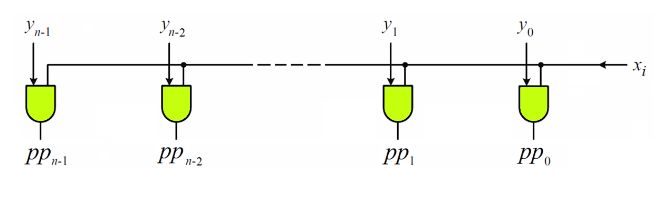 
2.3.2. 位串行乘法器
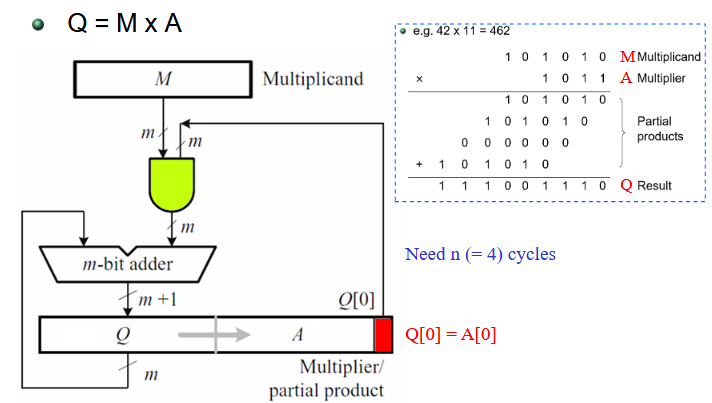首先，被乘数寄存器中会寄存被乘数 M，再将乘数 A寄存于乘数/部分积寄存器。每次计算，都会从乘数/部分积寄存器中取出第 0 位来进行部分积运算，并将得到的部分积与来自乘数/部分积寄存器的值（初始为 0）再进行一次加和之后，存入寄存器，并将整个寄存器向右移一位，由此完成一位乘数的乘法。
2.3.3. 阵列乘法器
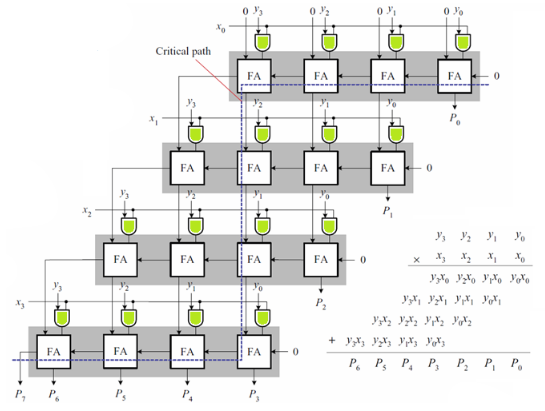整列乘法器在位串行乘法器的基础上，用阵列取代了移位，使得所有位的乘数和被乘数能同时进行与计算。随后进行三次部分积的加和即可得到结果。
在阵列乘法器中，关键路径在于最长的进位路径，如上图标注。有最长延迟为，
这个公式是根据下图推理出的，是简化
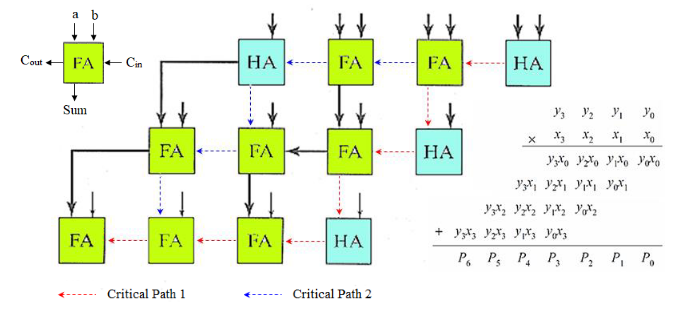M-1 是第一行 carry 只传 M-1 次，从最后一个 sum 下去。N-2 是因为第一行不用传 carry（因为输入进位是 0），最后一行不用传，因为直接输出 sum。最后的 sum 是 N-1，因为 N 行只用将部分积加和 N-1 次就能得出结果了。
2.3.4. 进位保留乘法器
但若注意到, 当使进位输出位如下图所示向下沿对角线通过而不只是向左通过时乘法的结果并不改变, 就可以得到一个更有效的实现。我们加入一个额外的加法器来产生最终的结果，这个加法器称为向量合并 (vector-merging) 加法器。
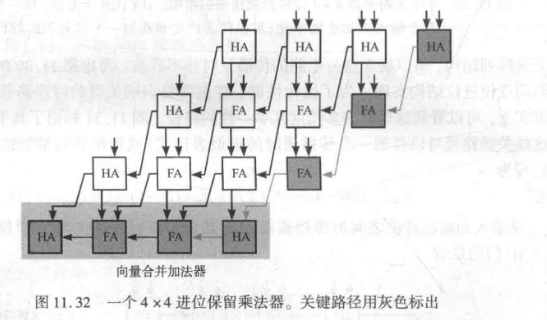虽然整体面积增加了，但是在最坏情形下关键路径最短且唯一确定。
假设
2.3.5. Wallace 树和 Dadda 树
他这个地方和书上不一样。
2.3.5.1. Wallace 树
部分和加法器可以设计成树形，可以减少关键路径和所需的加法器单元数目。根据点图，我们可以将点图重新安排成下图（b）中的树形，由此看出其深度。可以用全加器：三个输入和两个输出，一个输出和到当前列，一个输出进位到下一列；半加器：两个输入和两个输出。
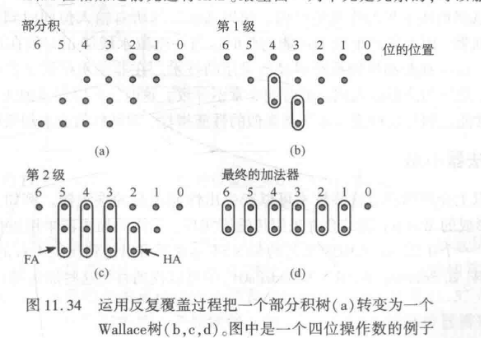总体的思路是，将树一步步从最深深度开始，逐级减小。首先是在最深和次深级用半加器，生成深度为 3 的树；随后使用 3 个全加器和 1 个半价器生成深度为 2 的树，最后用半加器完成计算。
传播延时为
2.3.5.2. Dadda 树
2.3.6. 有符号乘法器
回忆一下补码。
在有符号乘法器的设计中，需要将减去某数化成取反的形式，对于
4 位 Baugh-Wooley 阵列乘法器
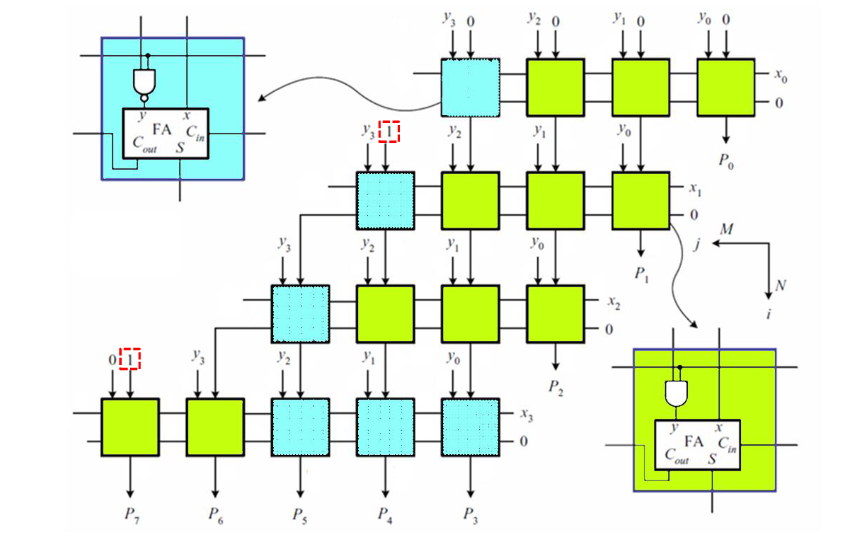
3. 数据通路结构中的功耗考虑
在 CMOS 设计中，功耗是电源 (
可以看出，如果降低工作电压能明显降低功耗，但是也会带来高延迟和性能损失。
为了补偿速度的降低，可以使用设计技巧。并行功能块在较低频率和较低
还有一些其他的技巧：
- 多种电源电压：以不同速度运行的模块可以使用不同的电源来运行。慢速模块可以在较低
下运行，而快速模块可以在较高 下运行 - 动态电压 (V) 和频率 (F) 缩放 (DVFS)：允许多个 F/V 对，针对的是整个系统。
- 掉电模式：放置不需要处理的模块处于待机模式
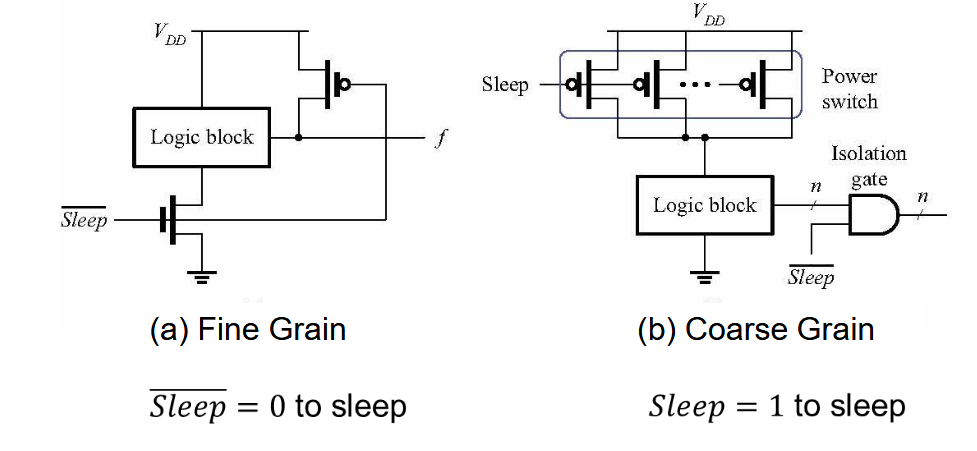
3.1. 时钟门控
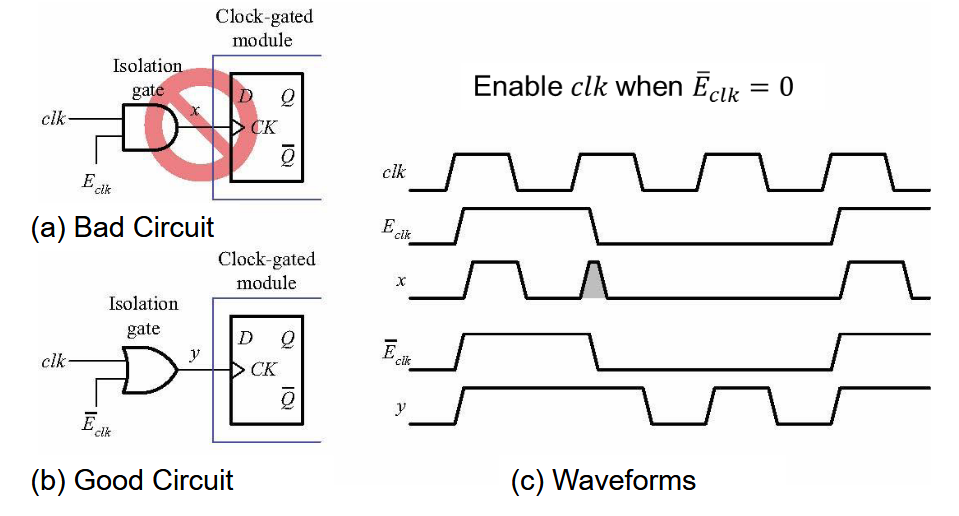
第一种电路可能造成错误的时钟信号，导致 FIFO 触发。
3.2. 电源门控
功率门控可有效降低功耗。
